График Турана - Turán graph

График Турана
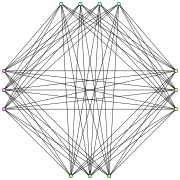Граф Турана T (13,4)
Названный в честь	Пал Туран
Вершины	п
Края	~${\displaystyle {\frac {(r-1)n^{2}}{2r}}}$
Радиус	${\displaystyle \left\{{\begin{array}{ll}\infty &r=1\\2&r\leq n/2\\1&{\text{otherwise}}\end{array}}\right.}$
Диаметр	${\displaystyle \left\{{\begin{array}{ll}\infty &r=1\\1&r=n\\2&{\text{otherwise}}\end{array}}\right.}$
Обхват	${\displaystyle \left\{{\begin{array}{ll}\infty &r=1\vee (n\leq 3\wedge r\leq 2)\\4&r=2\\3&{\text{otherwise}}\end{array}}\right.}$
Хроматическое число	р
Обозначение	Т(п,р)
Таблица графиков и параметров

В График Турана Т(п,р) это полный многодольный граф образована разбиение набора из п вершины в р подмножества с максимально равными размерами и соединяющими две вершины ребром тогда и только тогда, когда они принадлежат разным подмножествам. На графике будет ${\displaystyle (n\,{\bmod {\,}}r)}$ подмножества размера ${\displaystyle \lceil n/r\rceil }$, и ${\displaystyle r-(n\,{\bmod {\,}}r)}$ подмножества размера ${\displaystyle \lfloor n/r\rfloor }$. То есть это полный р-дольный граф

${\displaystyle K_{\lceil n/r\rceil ,\lceil n/r\rceil ,\ldots ,\lfloor n/r\rfloor ,\lfloor n/r\rfloor }.}$

Каждая вершина имеет степень либо ${\displaystyle n-\lceil n/r\rceil }$ или же ${\displaystyle n-\lfloor n/r\rfloor }$. Количество ребер

${\displaystyle {\frac {n(n-1)}{2}}-(n\,{\bmod {\,}}r){\frac {\lceil n/r\rceil (\lceil n/r\rceil -1)}{2}}-(r-(n\,{\bmod {\,}}r)){\frac {\lfloor n/r\rfloor (\lfloor n/r\rfloor -1)}{2}}\leq \left(1-{\frac {1}{r}}\right){\frac {n^{2}}{2}}.}$

Это регулярный граф если п делится на р.

Теорема Турана

Графы Турана названы в честь Пал Туран, кто использовал их, чтобы доказать Теорема Турана, важный результат в экстремальная теория графов.

По принципу ячейки, каждый набор р +1 вершина в графе Турана включает две вершины в одном подмножестве разбиения; следовательно, граф Турана не содержит клика размерар + 1. Согласно теореме Турана, граф Турана имеет максимально возможное количество ребер среди всех (р + 1) -бескликовые графы с п вершины. Кееваш и Судаков (2003) показывают, что граф Турана также является единственным (р + 1) -бескликовый граф порядка п в котором каждое подмножество αп вершины охватывают не менее ${\displaystyle {\frac {r\,{-}\,1}{3r}}(2\alpha -1)n^{2}}$ ребер, если α достаточно близко к 1. Теорема Эрдеша – Стоуна расширяет теорему Турана, ограничивая количество ребер в графе, не имеющем фиксированного графа Турана в качестве подграфа. С помощью этой теоремы аналогичные оценки в экстремальной теории графов могут быть доказаны для любого исключенного подграфа в зависимости от хроматическое число подграфа.

Особые случаи

В октаэдр, а 3-кросс-многогранник чьи ребра и вершины образуют K_2,2,2, граф Турана Т(6,3). Несвязанные вершины имеют одинаковый цвет в этой гранецентрированной проекции.

Несколько вариантов параметра р в графе Турана приводят к заметным графам, которые были изучены независимо.

Граф Турана Т(2п,п) может быть образована удалением идеальное соответствие из полный график K_2п. В качестве Робертс (1969) показал, что этот график коробочка точно п; это иногда называют Граф Робертса. Этот график также является 1-скелет из п-размерный кросс-многогранник; например, график Т(6,3) = K_2,2,2 это октаэдрический граф, график регулярного октаэдр. Если п пары идут на вечеринку, и каждый человек пожимает руку каждому, кроме своего партнера, тогда этот график описывает набор происходящих рукопожатий; по этой причине его также называют график коктейльной вечеринки.

Граф Турана Т(п, 2) является полный двудольный граф и когда п чётно Граф Мура. Когда р является делителем п, граф Турана симметричный и строго регулярный, хотя некоторые авторы считают графы Турана тривиальным случаем сильной регулярности и поэтому исключают их из определения сильно регулярного графа.

Граф Турана ${\displaystyle T(n,\lceil n/3\rceil )}$ имеет 3^а2^б максимальные клики, где3а + 2б = п и б ≤ 2; каждая максимальная клика формируется путем выбора одной вершины из каждого подмножества разбиения. Это максимально возможное количество максимальных клик среди всех п-вершинные графы независимо от количества ребер в графе (Moon and Moser 1965); эти графики иногда называют Графики Луны – Мозера.

Другие свойства

Каждый граф Турана является cograph; то есть он может быть образован из отдельных вершин последовательностью несвязный союз и дополнять операции. В частности, такая последовательность может начинаться с формирования каждого из независимых наборов графа Турана как непересекающегося объединения изолированных вершин. Тогда общий граф является дополнением несвязного объединения дополнений этих независимых множеств.

Чао и Новаки (1982) показывают, что графы Турана являются хроматически уникальный: нет других графиков аналогичных хроматические полиномы. Никифоров (2005) использует графы Турана для получения нижней оценки суммы kth собственные значения графа и его дополнения.

Фоллс, Пауэлл и Сноиинк разрабатывают эффективный алгоритм для поиска кластеров ортологичных групп генов в данных генома путем представления данных в виде графика и поиска больших подграфов Турана.

Графы Турана также обладают некоторыми интересными свойствами, связанными с геометрическая теория графов. Пор и Вуд (2005) дают нижнюю оценку Ω ((rn)^3/4) по объему любого трехмерного встраивание сетки графа Турана. Витсенхаузен (1974) предполагает, что максимальная сумма квадратов расстояний среди п точки с единичным диаметром в р^d, достигается для конфигурации, образованной вложением графа Турана в вершины регулярного симплекса.

An п-вершинный граф грамм это подграф графа Турана Т(п,р) если и только если грамм признает справедливая окраска с р цвета. Разбиение графа Турана на независимые множества соответствует разбиению грамм в цветовые классы. В частности, граф Турана является единственным максимальным п-вершинный граф с р-цветная ровная окраска.

Рекомендации

• Chao, C. Y .; Новацкий, Г. А. (1982). «О максимально насыщенных графах». Дискретная математика. 41 (2): 139–143. Дои:10.1016 / 0012-365X (82) 90200-X.
• Falls, Крейг; Пауэлл, Брэдфорд; Snoeyink, Джек. «Вычисление COG высокой строгости с использованием графов типа Турана» (PDF).
• Кееваш, Питер; Судаков, Бенни (2003). «Локальная плотность в графах с запрещенными подграфами» (PDF). Комбинаторика, теория вероятностей и вычисления. 12 (2): 139–153. Дои:10.1017 / S0963548302005539.
• Moon, J. W .; Мозер, Л. (1965). «По кликам в графах». Израильский математический журнал. 3: 23–28. Дои:10.1007 / BF02760024.
• Никифоров, Владимир (2005). «Задачи на собственные значения типа Нордхауза-Гаддума». arXiv:math.CO/0506260.
• Пор, Аттила; Вуд, Дэвид Р. (2005). «Нет-тройка в строке в 3D». Proc. Int. Symp. Графический рисунок (GD 2004). Конспект лекций по информатике No. 3383, Springer-Verlag. С. 395–402. Дои:10.1007 / b105810. HDL:11693/27422.
• Робертс, Ф.С. (1969). Тутте, W.T. (ред.). «О коробчатости и кубичности графа». Недавний прогресс в комбинаторике: 301–310.
• Туран, П. (1941). «Egypt gráfelméleti szélsőértékfeladatról (Об одной экстремальной задаче в теории графов)». Matematikai és Fizikai Lapok. 48: 436–452.
• Витсенхаузен, Х. С. (1974). «На максимуме суммы квадратов расстояний при ограничении диаметра». Американский математический ежемесячный журнал. 81 (10): 1100–1101. Дои:10.2307/2319046. JSTOR  2319046.

внешняя ссылка

• Вайсштейн, Эрик В. "График коктейльной вечеринки". MathWorld.
• Вайсштейн, Эрик В. «Октаэдрический график». MathWorld.
• Вайсштейн, Эрик В. "График Турана". MathWorld.