Точка застоя потока - Stagnation point flow

В динамика жидкостей, Точка застоя потока представляет собой поток жидкости в непосредственной близости от твердой поверхности, на котором жидкость, приближающаяся к поверхности, разделяется на различные потоки или встречные потоки жидкости, встречающиеся в экспериментах. Хотя жидкость застаивается повсюду на твердой поверхности из-за условие противоскольжения, название точка застоя относится к точкам застоя невязких Эйлер решения.

Поток Hiemenz^[1][2]

Двумерный поток точки застоя

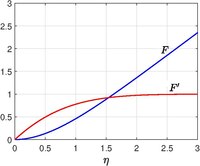
Hiemenz^[3] сформулировал задачу и численно рассчитал решение в 1911 г., а затем Лесли Ховарт (1934).^[4] Течение в окрестности точки торможения можно смоделировать потоком к бесконечной плоской пластине, даже если все тело изогнуто (эффекты локальной кривизны незначительны). Пусть тарелка будет в ${\displaystyle xz}$ самолет с ${\displaystyle (x,y)=(0,0)}$ представляющий точку застоя. Невязкий функция потока ${\displaystyle \psi }$ и скорость ${\displaystyle (u,v)}$ из Потенциальный поток теория

${\displaystyle \psi =kxy,\quad u=kx,\quad v=-ky}$

куда ${\displaystyle k}$ - произвольная константа (представляет собой скорость деформации в противоточной установке). Для реальной жидкости (включая вязкие эффекты) существует автомодельное решение, если определить

${\displaystyle \eta ={\sqrt {\frac {k}{\nu }}}y,\quad \psi ={\sqrt {\nu k}}xF(\eta )}$

куда ${\displaystyle \nu }$ это Кинематическая вязкость и ${\displaystyle \delta ={\sqrt {\nu /k}}}$ это толщина пограничного слоя но он постоянен (завихренность, возникающая на твердой поверхности, предотвращается удалением из-за встречной конвекции, аналогичные профили Пограничный слой Блазиуса с всасыванием, Вихревой поток фон Кармана так далее.,). Тогда компоненты скорости, а затем давление и уравнение для ${\displaystyle F(\eta )}$ с помощью Уравнения Навье – Стокса находятся

${\displaystyle u=kxF',\quad v=-{\sqrt {\nu k}}F,\quad {\frac {p_{o}-p}{\rho }}={\frac {1}{2}}k^{2}x^{2}+k\nu F'+{\frac {1}{2}}k\nu F^{2}}$

${\displaystyle F'''+FF''-F'^{2}+1=0}$

и граничное условие из-за отсутствия проникновения и прилипания и условие набегающего потока для ${\displaystyle u}$(Обратите внимание на граничные условия для ${\displaystyle v}$ далеко от пластины не указывается, потому что это часть решения - типичная проблема пограничного слоя)

${\displaystyle F(0)=0,\ F'(0)=0,F'(\infty )=1.}$

Сформулированная здесь проблема является частным случаем Пограничный слой Фолкнера-Скан. Асимптотики для больших ${\displaystyle \eta \rightarrow \infty }$ находятся

${\displaystyle F\sim \eta -0.6479,\quad u\sim kx,\quad v\sim -k(y-\delta ^{*}),\quad \delta ^{*}=0.6479\delta }$

куда ${\displaystyle \delta ^{*}}$ это толщина вытеснения.

Точка застоя потока с перемещающей пластиной^[5]

Течение точки торможения с движущейся пластиной с постоянной скоростью ${\displaystyle U}$ может рассматриваться как модель для вращающихся твердых тел вблизи точек торможения. Функция потока

${\displaystyle \psi ={\sqrt {\nu k}}xF(\eta )+U\delta \int _{0}^{\eta }G(\eta )d\eta }$

куда ${\displaystyle G(\eta )}$ удовлетворяет уравнению

${\displaystyle G''+FG'-F'G=0,\quad G(0)=1,\quad G(\infty )=0}$

и Ротт (1956)^[6] дал решение как ${\displaystyle G(\eta )={\frac {F''(\eta )}{F''(0)}}.}$

Наклонный поток точки застоя

Предыдущий анализ предполагает, что поток встречает нормальное направление. Функция невязкого потока для потока в наклонной точке застоя получается добавлением постоянного завихренность ${\displaystyle -\zeta _{o}}$.

${\displaystyle \psi =kxy+{\frac {1}{2}}\zeta _{o}y^{2}}$

Соответствующий анализ для вязкой жидкости изучен Стюартом (1959),^[7] Тамада (1979)^[8] и Доррепаал (1986).^[9] Самоподобная функция потока:

${\displaystyle \psi ={\sqrt {\nu k}}xF(\eta )+\zeta _{o}\delta ^{2}\int _{0}^{\eta }H(\eta )d\eta }$

куда ${\displaystyle H(\eta )}$ удовлетворяет уравнению

${\displaystyle H''+FH'-F'H=0,\quad H(0)=0,\quad H'(\infty )=1}$.

Homann Flow

Поток Хоманна с впрыском

Поток Homann с всасыванием

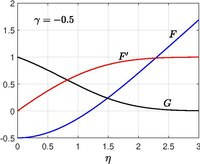
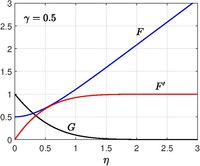
Соответствующая задача в осесимметричной координате решена Хоманном (1936).^[10] и это служит моделью для обтекания сферы вблизи точки торможения. Пол А. Либби (1974)^[11](1976)^[12] рассмотренное течение Гоманна с постоянно движущейся пластиной со скоростью ${\displaystyle U}$ а также допускается всасывание / впрыскивание со скоростью ${\displaystyle V}$ на поверхности.

Автомодельное решение получается путем введения следующего преобразования для скорости ${\displaystyle (v_{r},v_{\theta },v_{z})}$ в цилиндрических координатах

${\displaystyle \eta ={\sqrt {\frac {k}{\nu }}}z,\quad \gamma =-{\frac {V}{2{\sqrt {k\nu }}}},\quad v_{r}=krF'(\eta )+U\cos \theta G(\eta ),\quad v_{\theta }=-U\sin \theta G(\eta ),\quad v_{z}=-2{\sqrt {k\nu }}F(\eta )}$

а давление определяется выражением

${\displaystyle {\frac {p-p_{o}}{\rho }}=-{\frac {1}{2}}k^{2}r^{2}-2k\nu (F^{2}+F')}$

Следовательно Уравнения Навье – Стокса сократить до

${\displaystyle {\begin{aligned}F'''+2FF''-F'^{2}+1&=0,\\G''+2FG'-F'G&=0\end{aligned}}}$

с граничными условиями,

${\displaystyle F(0)=\gamma ,\quad F'(0)=0,\quad F'(\infty )=1,\quad G(0)=1,\quad G(\infty )=0.}$

Когда ${\displaystyle U=V=0}$, восстанавливается классическая проблема Хоманна.

Противотоки самолета

Струи, выходящие из щелевых струй, создают промежуточную точку застоя согласно теории потенциала. Течение вблизи точки торможения можно исследовать с помощью автомодельного решения. Эта установка широко используется в горение эксперименты. Первоначальное исследование набегающих стагнационных потоков принадлежит К.Ю. Ван.^[13][14] Пусть две жидкости с постоянными свойствами обозначены суффиксом ${\displaystyle 1({\text{top}}),\ 2({\text{bottom}})}$ течет из противоположного направления, и давайте предположим, что две жидкости не смешиваются, а граница раздела (расположена в ${\displaystyle y=0}$) плоский. Скорость определяется как

${\displaystyle u_{1}=k_{1}x,\quad v_{1}=-k_{1}y,\quad u_{2}=k_{2}x,\quad v_{2}=-k_{2}y}$

куда ${\displaystyle k_{1},\ k_{2}}$ скорости деформации жидкостей. На границе раздела скорости, касательное напряжение и давление должны быть непрерывными. Введя автомодельное преобразование,

${\displaystyle \eta _{1}={\sqrt {\frac {\nu _{1}}{k_{1}}}}y,\quad u_{1}=k_{1}xF_{1}',\quad v_{1}=-{\sqrt {\nu _{1}k_{1}}}F_{1}}$

${\displaystyle \eta _{2}={\sqrt {\frac {\nu _{2}}{k_{2}}}}y,\quad u_{2}=k_{2}xF_{2}',\quad v_{2}=-{\sqrt {\nu _{2}k_{2}}}F_{2}}$

уравнения результатов,

${\displaystyle F_{1}'''+F_{1}F_{1}''-F_{1}'^{2}+1=0,\quad {\frac {p_{o1}-p_{1}}{\rho _{1}}}={\frac {1}{2}}k_{1}^{2}x^{2}+k_{1}\nu _{1}F_{1}'+{\frac {1}{2}}k_{1}\nu _{1}F_{1}^{2}}$

${\displaystyle F_{2}'''+F_{2}F_{2}''-F_{2}'^{2}+1=0,\quad {\frac {p_{o2}-p_{2}}{\rho _{2}}}={\frac {1}{2}}k_{2}^{2}x^{2}+k_{2}\nu _{2}F_{2}'+{\frac {1}{2}}k_{2}\nu _{2}F_{2}^{2}.}$

Условие непроникания на границе раздела и условие набегающего потока вдали от плоскости торможения становятся

${\displaystyle F_{1}(0)=0,\quad F_{1}'(\infty )=1,\quad F_{2}(0)=0,\quad F_{2}'(-\infty )=1.}$

Но уравнения требуют еще двух граничных условий. В ${\displaystyle \eta =0}$, тангенциальные скорости ${\displaystyle u_{1}=u_{2}}$, касательное напряжение ${\displaystyle \rho _{1}\nu _{1}\partial u_{1}/\partial y=\rho _{2}\nu _{2}\partial u_{2}/\partial y}$ и давление ${\displaystyle p_{1}=p_{2}}$ непрерывны. Следовательно,

${\displaystyle {\begin{aligned}k_{1}F_{1}'(0)&=k_{2}F_{2}'(0),\\\rho _{1}{\sqrt {\nu _{1}k_{1}^{3}}}F_{1}''(0)&=\rho _{2}{\sqrt {\nu _{2}k_{2}^{3}}}F_{2}''(0),\\p_{o1}-\rho _{1}\nu _{1}k_{1}F_{1}'(0)&=p_{o2}-\rho _{2}\nu _{2}k_{2}F_{2}'(0).\end{aligned}}}$

куда ${\displaystyle \rho _{1}k_{1}^{2}=\rho _{2}k_{2}^{2}}$(от внешней невязкой проблемы) используется. Обе ${\displaystyle F_{i}'(0),F_{i}''(0)}$ не известны априори, но получено из условий сопоставления. Третье уравнение определяет изменение внешнего давления ${\displaystyle p_{o1}-p_{o2}}$ из-за эффекта вязкости. Итак, есть только два параметра, которые управляют потоком:

${\displaystyle \Lambda ={\frac {k_{1}}{k_{2}}}=\left({\frac {\rho _{2}}{\rho _{1}}}\right)^{1/2},\quad \Gamma ={\frac {\nu _{2}}{\nu _{1}}}}$

то граничные условия становятся

${\displaystyle F_{1}'(0)=\Lambda F_{2}'(0),\quad F_{1}''(0)={\sqrt {\frac {\Gamma }{\Lambda }}}F_{2}''(0)}$.

Постоянная плотность и постоянная вязкость

Когда плотности и вязкости двух сталкивающихся струй одинаковы и постоянны, скорость деформации также постоянна. ${\displaystyle k_{1}=k_{2}=k}$ а решение потенциального потока становится решением уравнений Навье-Стокса, т. е.

${\displaystyle u=kx,\quad v=-ky}$

везде в области потока. Керр и Долд нашли дополнительное новое решение, названное Вихрь Керра – Дольда уравнений Навье-Стокса в 1994 г. в виде периодического массива стационарных вихрей, наложенных на противоточные струи постоянной плотности и постоянной вязкости.^[15]

Рекомендации

1. Розенхед, Луи, изд. Ламинарные пограничные слои. Кларендон Пресс, 1963 год.
2. Бэтчелор, Джордж Кейт. Введение в гидродинамику. Издательство Кембриджского университета, 2000.
3. Хиеменц, Карл. Die Grenzschicht an einem in den gleichförmigen Flüssigkeitsstrom eingetauchten geraden Kreiszylinder ... Diss. 1911 г.
4. Ховарт, Лесли. О расчете установившегося течения в пограничном слое у поверхности цилиндра в потоке. № ARC-R / M-1632. СОВЕТ АЭРОНАВИГАЦИОННЫХ ИССЛЕДОВАНИЙ ЛОНДОН (ВЕЛИКОБРИТАНИЯ), 1934 год.
5. Дразин, Филип Г., и Норман Райли. Уравнения Навье – Стокса: классификация потоков и точные решения. № 334. Издательство Кембриджского университета, 2006.
6. Ротт, Николас. «Нестационарное вязкое течение вблизи точки торможения». Ежеквартальный вестник прикладной математики 13,4 (1956): 444–451.
7. Стюарт, Дж. Т. «Вязкое течение вблизи точки торможения, когда внешний поток имеет однородную завихренность». Журнал аэрокосмических наук (2012).
8. Тамада, Ко. «Двумерный застойный поток, косо падающий на плоскую стенку». Журнал Физического общества Японии 46 (1979): 310.
9. Доррепаал, Дж. М. «Точное решение уравнения Навье – Стокса, которое описывает неортогональный поток в точке остановки в двух измерениях». Журнал гидромеханики 163 (1986): 141–147.
10. Хоманн, Фриц. "Der Einfluss grosser Zähigkeit bei der Strömung um den Zylinder und um die Kugel". ZAMM ‐ Journal of Applied Mathematics and Mechanics / Zeitschrift für Angewandte Mathematik und Mechanik 16.3 (1936): 153–164.
11. Либби, Пол А. «Стена сдвигается в трехмерной точке застоя с движущейся стенкой». Журнал AIAA 12.3 (1974): 408–409.
12. Либби, Пол А. «Ламинарный поток в трехмерной точке застоя с большой скоростью нагнетания». AIAA Journal 14.9 (1976): 1273–1279.
13. Ван, К. Я. «Застойное течение на поверхности неподвижной жидкости - точное решение уравнений Навье-Стокса». Ежеквартальный вестник прикладной математики 43.2 (1985): 215–223.
14. Ван, К. Я. "Встречные стагнационные потоки". Физика жидкостей 30.3 (1987): 915–917.
15. Керр, О.С., и Долд, Дж. У. (1994). Периодические установившиеся вихри в застойном потоке. Журнал гидромеханики, 276, 307-325.