Многогранник с накоплением - Stacked polytope

В многогранная комбинаторика (раздел математики), сложенный многогранник это многогранник сформированный из симплекс путем многократного приклеивания другого симплекса к одному из грани.^[1]^[2]

Примеры

Каждый симплекс сам по себе является многогранником с накоплением.

В трех измерениях каждый сложенный многогранник является многогранник с треугольными гранями и несколько дельтаэдры (многогранники с равносторонний треугольник грани) являются сложенными многогранниками

Четырехугольный тетраэдр слева представляет собой многогранник с накоплением, но пятиугольная бипирамида справа нет

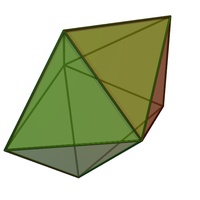
В многограннике с накоплением каждый новый добавленный симплекс может касаться только одной из граней предыдущих. Так, например, четырехугольный тетраэдр, форма, образованная склеиванием пяти правильных тетраэдров вокруг общего отрезка прямой, представляет собой сложенный многогранник (у него есть небольшой промежуток между первым и последним тетраэдрами). Однако похожие на пятиугольная бипирамида не является сложенным многогранником, потому что, если он образован склейкой тетраэдров вместе, последний тетраэдр будет приклеен к двум треугольным граням предыдущих тетраэдров, а не только к одной.

Другие невыпуклые сложенные дельтаэдры включают:

Три тетраэдра	Четыре тетраэдра	Пять тетраэдров

Комбинаторная структура

An Аполлоническая сеть, график сложенного многогранника

В неориентированный граф образованный вершинами и ребрами сложенного многогранника в d размеры - это (d + 1) -дерево. Точнее, графы сложенных многогранников - это в точности (d + 1) -деревья, в которых каждое d-вертекс клика (полный подграф) содержится не более чем в двух (d + 1) -вершинные клики.^[3] Например, графики трехмерных сложенных многогранников - это в точности Аполлонические сети, графы образованы из треугольника путем многократного деления треугольной грани графа на три меньших треугольника.

Одна из причин важности сложенных многогранников заключается в том, что среди всех d-размерный симплициальные многогранники с заданным числом вершин многогранники с накоплением имеют наименьшее возможное количество граней более высокой размерности. Для трехмерных симплициальных многогранников количество ребер и двумерных граней определяется из числа вершин по формуле Формула Эйлера независимо от того, сложен ли многогранник в стопку, но это не так в высших измерениях. Аналогично, симплициальные многогранники, которые максимизируют количество граней более высокой размерности для их числа вершин, являются циклические многогранники.^[2]

Рекомендации

^ Грюнбаум, Бранко (2001), «Выпуклый многогранник, не равносоставимый» (PDF), Геомбинаторика, 10 (4): 165–171, МИСТЕР 1825338
^ ^а ^б Миллер, Эзра; Райнер, Виктор; Штурмфельс, Бернд, Геометрическая комбинаторика, IAS / Серия математических наук Парк-Сити, 13, Американское математическое общество, стр. 621, г. ISBN 9780821886953.
^ Кох, Этан; Перлес, Миха А. (1976), "Эффективность покрытия деревьев и k-деревья », Труды Седьмой Юго-Восточной конференции по комбинаторике, теории графов и вычислениям (Университет штата Луизиана, Батон-Руж, штат Луизиана, 1976 г.), Congressus Numerantium, Виннипег, Манитоба, Канада: Utilitas Mathematica, 17: 391–420, МИСТЕР 0457265. См., В частности, стр. 420.

[g-1] Грюнбаум, Бранко (2001), «Выпуклый многогранник, не равносоставимый» (PDF), Геомбинаторика, 10 (4): 165–171, МИСТЕР 1825338

[gc-2] а ^б Миллер, Эзра; Райнер, Виктор; Штурмфельс, Бернд, Геометрическая комбинаторика, IAS / Серия математических наук Парк-Сити, 13, Американское математическое общество, стр. 621, г. ISBN 9780821886953.

[3] Кох, Этан; Перлес, Миха А. (1976), "Эффективность покрытия деревьев и k-деревья », Труды Седьмой Юго-Восточной конференции по комбинаторике, теории графов и вычислениям (Университет штата Луизиана, Батон-Руж, штат Луизиана, 1976 г.), Congressus Numerantium, Виннипег, Манитоба, Канада: Utilitas Mathematica, 17: 391–420, МИСТЕР 0457265. См., В частности, стр. 420.

[1]

[2]

[3]