Устойчивость Солнечной системы - Stability of the Solar System

В стабильность Солнечной системы является предметом многих исследований в астрономия. Хотя планеты были стабильными, когда исторически наблюдались, и будут в краткосрочной перспективе, их слабое гравитационное влияние друг на друга может складываться непредсказуемым образом. По этой причине (среди прочего) Солнечная система хаотичен в техническом смысле математического теория хаоса,[1] и даже самые точные долгосрочные модели орбитального движения Солнечной системы недействительны более чем на несколько десятков миллионов лет.[2]

Солнечная система устойчива с точки зрения человека и далеко за ее пределами, учитывая, что маловероятно, что какие-либо планеты столкнутся друг с другом или будут выброшены из системы в следующие несколько миллиардов лет.[3] и Орбита Земли будет относительно стабильным.[4]

С Закон всемирного тяготения Ньютона (1687), математики и астрономы (такие как Пьер-Симон Лаплас, Жозеф Луи Лагранж, Карл Фридрих Гаусс, Анри Пуанкаре, Андрей Колмогоров, Владимир Арнольд, и Юрген Мозер ) искали доказательства стабильности движения планет, и этот поиск привел к множеству математических разработок и нескольким последовательным «доказательствам» стабильности Солнечной системы.[5]

Обзор и проблемы

Основная статья: проблема н-тела

Орбиты планет открыты для долгосрочных изменений. Моделирование Солнечной системы - это случай ппроблема тела физики, которая обычно неразрешима, кроме как с помощью численного моделирования.

Резонанс

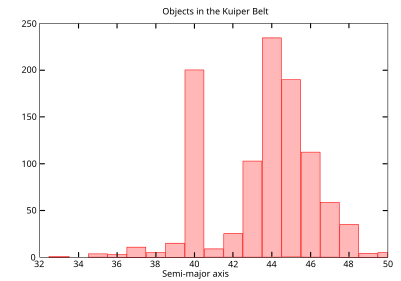
График, показывающий количество Пояс Койпера объекты на заданном расстоянии (в AU ) от солнца

Орбитальный резонанс происходит, когда любые два периода имеют простое числовое соотношение. Самый фундаментальный период для объекта Солнечной системы - это его орбитальный период, а орбитальные резонансы пронизывают Солнечную систему. В 1867 году американский астроном Дэниел Кирквуд заметил, что астероиды в пояс астероидов не распределяются случайным образом.[6] В поясе были отчетливые зазоры в местах, соответствующих резонансам с Юпитер. Например, не было астероидов в резонансе 3: 1 - на расстоянии 2,5 а.е. - или в резонансе 2: 1 на 3,3 а.е. (а.е. астрономическая единица, или, по сути, расстояние от Солнца до Земли). Теперь они известны как Пробелы Кирквуда. Позже было обнаружено, что некоторые астероиды вращаются по орбите в этих промежутках, но их орбиты нестабильны, и в конечном итоге они вырвутся из резонанса из-за близких столкновений с большой планетой.

Другой распространенной формой резонанса в Солнечной системе является спин-орбитальный резонанс, когда период вращение (время, за которое планета или луна совершает один оборот вокруг своей оси) имеет простую числовую связь с ее орбитальным периодом. Пример наш собственный Луна, который находится в спин-орбитальном резонансе 1: 1, сохраняющем обратная сторона луны подальше от земной шар. Меркурий находится в спин-орбитальном резонансе 3: 2.

Предсказуемость

Орбиты планет хаотичны в более длительных временных масштабах, так что вся Солнечная система обладает Ляпуновское время в диапазоне 2–230 млн лет.[3] Во всех случаях это означает, что положение планеты на ее орбите в конечном итоге невозможно предсказать с какой-либо уверенностью (поэтому, например, становится неопределенным время зимы и лета), но в некоторых случаях сами орбиты могут резко измениться. Такой хаос наиболее сильно проявляется в изменении эксцентриситет, при этом орбиты некоторых планет становятся значительно больше или меньшеэллиптический.[7]

В расчет неизвестные включают астероиды, солнечная квадрупольный момент, потеря массы от солнце через радиацию и Солнечный ветер, сопротивление солнечного ветра на планетарной магнитосферы, галактический приливные силы, и эффекты от прохождения звезды.[8]

Сценарии

Резонанс Нептуна-Плутона

В Нептун –Плутон система лежит в соотношении 3: 2 орбитальный резонанс. Си Джей Коэн и Э. К. Хаббард на Военно-морской центр наземной войны Дальгрен Дивизия открыл это в 1965 году. Хотя сам резонанс будет оставаться стабильным в краткосрочной перспективе, становится невозможным предсказать положение Плутона с какой-либо степенью точности, поскольку неопределенность положения увеличивается в несколько раз. е с каждым Ляпуновское время, что для Плутона на 10–20 миллионов лет вперед.[9]Таким образом, в масштабе времени в сотни миллионов лет орбитальную фазу Плутона невозможно определить, даже если орбита Плутона кажется совершенно стабильной на 10 °. MYR шкалы времени (Ито и Таникава 2002, MNRAS).

Юпитерианский лунный резонанс

Спутник Юпитера Ио имеет орбитальный период 1,769 дня, что почти вдвое меньше, чем у следующего спутника Европа (3.551 дней). Они находятся в резонансе орбита / орбита 2: 1. Этот конкретный резонанс имеет важные последствия, потому что гравитация Европы возмущает орбита Ио. По мере того, как Ио приближается к Юпитеру, а затем все дальше удаляется по орбите, он испытывает значительные приливные напряжения, приводящие к действию вулканов. Европа также находится в резонансе 2: 1 со следующим спутником. Ганимед.

Перигелий-прецессионный резонанс Меркурий-Юпитер 1: 1

Планета Меркурий особенно восприимчив к Юпитер влияние из-за небольшого небесного совпадения: Меркурия перигелий, точка, в которой он приближается к Солнцу, прецессирует со скоростью примерно 1,5 градуса каждые 1000 лет, а перигелий Юпитера прецессирует лишь немного медленнее. В какой-то момент они могут синхронизироваться, и тогда постоянные гравитационные тяги Юпитера могут накапливаться и сбивать Меркурий с курса с вероятностью 1–2% на 3–4 миллиарда лет в будущем. Это может полностью выбросить его из Солнечной системы.[1] или отправить его на встречный курс с Венера, Солнце или Земля.[10]

Влияние астероидов

Хаос от геологических процессов

Другой пример - земной осевой наклон которые из-за трения, возникающего внутри Земли мантия приливными взаимодействиями с Луна (Смотри ниже ), будет хаотичным в какой-то момент между 1,5 и 4,5 миллиардами лет.[11]

Смотрите также: Гипотеза сдвига полюсов

Внешние воздействия

На него также могут повлиять объекты, приходящие извне Солнечной системы. Хотя технически они не являются частью Солнечной системы для целей изучения внутренней стабильности системы, они, тем не менее, могут изменить систему. К сожалению, предсказывая потенциальное влияние этих внесолнечные объекты это даже сложнее, чем предсказать влияние объектов в системе просто из-за огромных расстояний. Среди известных объектов, способных существенно повлиять на Солнечную систему, есть звезда Gliese 710, который, как ожидается, пройдет около системы примерно через 1,281 миллиона лет.[12] Хотя ожидается, что звезда не окажет существенного влияния на орбиты основных планет, она может существенно разрушить облако Оорта, что может вызвать большую активность комет во всей Солнечной системе. Есть, по крайней мере, дюжина других звезд, которые потенциально могут сблизиться в ближайшие несколько миллионов лет.[13]

Исследования

LONGSTOP

Проект LONGSTOP (Долгосрочное гравитационное исследование внешних планет) представлял собой международный консорциум специалистов по динамике Солнечной системы 1982 года, возглавляемый Арчи Рой. Это включало создание модели на суперкомпьютере, объединяющей орбиты (только) внешних планет. Его результаты показали несколько любопытных обменов энергией между внешними планетами, но никаких признаков явной нестабильности.

Цифровая Оррери

Другой проект заключался в создании Digital Orrery компанией Джерри Сассман и его группа Массачусетского технологического института в 1988 году. Группа использовала суперкомпьютер для интегрирования орбит внешних планет на протяжении 845 миллионов лет (около 20 процентов возраста Солнечной системы). В 1988 году Сассман и Уисдом с помощью Оррери обнаружили данные, которые показали, что орбита Плутона демонстрирует признаки хаоса, отчасти из-за его специфических особенностей. резонанс с Нептун.[9]

Если орбита Плутона хаотична, то технически вся Солнечная система хаотична, потому что каждое тело, даже такое маленькое, как Плутон, в некоторой степени влияет на другие посредством гравитационного взаимодействия.[14]

Ласкар # 1

В 1989 г. Жак Ласкар из Бюро долгот в Париже опубликовал результаты своего численного интегрирования Солнечной системы за 200 миллионов лет. Это были не полные уравнения движения, а скорее усредненные уравнения, аналогичные тем, которые использовались Лаплас. Работа Ласкара показала, что орбита Земли (а также орбиты всех внутренних планет) хаотична и что ошибка в 15 метров при измерении положения Земли сегодня сделает невозможным предсказать, где будет Земля. его орбита прошло чуть более 100 миллионов лет.

Ласкар и Гастино

Жак Ласкар и его коллега Микаэль Гастино в 2008 году применили более тщательный подход, непосредственно смоделировав 2500 возможных вариантов будущего. Каждый из 2500 случаев имеет немного разные начальные условия: положение Меркурия варьируется примерно на 1 метр между одной симуляцией и другой.[15] В 20 случаях Меркурий выходит на опасную орбиту и часто сталкивается с Венерой или погружается в Солнце. Двигаясь по такой искривленной орбите, гравитация Меркурия с большей вероятностью заставит другие планеты сбиться с их постоянных путей: в одном смоделированном случае его возмущения отправили Марс в сторону Земли.[16]

Батыгин и Лафлин

Независимо от Ласкара и Гастино, Батыгин и Лафлин также напрямую моделировали Солнечную систему на 20 млрд лет в будущем. Их результаты пришли к тем же основным выводам, что и Ласкар и Гастино, но дополнительно предоставили нижнюю границу в миллиард (1e ^ 9) лет динамической продолжительности жизни Солнечной системы.[17]

Браун и Рейн

В 2020 году Гаретт Браун и Ханно Рейн из Университет Торонто опубликовали результаты своего численного интегрирования Солнечной системы за 5 миллиардов лет. Их работа показала, что орбита Меркурия очень хаотична и что ошибка в 0,38 миллиметра при измерении положения Меркурия сегодня сделает невозможным предсказать эксцентриситет его орбиты всего за 200 миллионов лет.[18]

Смотрите также

Рекомендации

[12]

  1. ^ а б Дж. Ласкар (1994). «Масштабный хаос в Солнечной системе». Астрономия и астрофизика. 287: L9 – L12. Bibcode:1994A & A ... 287L ... 9L.
  2. ^ Laskar, J .; П. Робутель; Ф. Жутель; М. Гастино; и другие. (2004). «Долгосрочное численное решение для инсоляционных величин Земли» (PDF). Астрономия и астрофизика. 428 (1): 261. Bibcode:2004A&A ... 428..261L. Дои:10.1051/0004-6361:20041335.
  3. ^ а б Уэйн Б. Хейс (2007). «Хаотична внешняя Солнечная система?». Природа Физика. 3 (10): 689–691. arXiv:astro-ph / 0702179. Bibcode:2007НатФ ... 3..689ч. Дои:10.1038 / nphys728.
  4. ^ Гриббин, Джон. Глубокая простота. Случайный дом 2004.
  5. ^ Ласкар, Жак (2000), Солнечная система: стабильность, Bibcode:2000eaa..bookE2198L
  6. ^ Холл, Нина (1994-09-01). Изучение хаоса. п. 110. ISBN  9780393312263.
  7. ^ Ян Стюарт (1997). Играет ли Бог в кости? (2-е изд.). Книги о пингвинах. С. 246–249. ISBN  978-0-14-025602-4.
  8. ^ Шина (17.09.2012). «Стабильность солнечной системы». SlideServe. Получено 2017-10-26.
  9. ^ а б Джеральд Джей Сассман; Джек Уиздом (1988). «Численное свидетельство того, что движение Плутона хаотично» (PDF). Наука. 241 (4864): 433–437. Bibcode:1988Научный ... 241..433S. Дои:10.1126 / science.241.4864.433. HDL:1721.1/6038. PMID  17792606.
  10. ^ Дэвид Шига (23 апреля 2008 г.). "Солнечная система может выйти из строя прежде, чем Солнце умрет". Служба новостей NewScientist.com. В архиве из оригинала 31.12.2014. Получено 2015-03-31.
  11. ^ О. Нерон де Сюрджи; Дж. Ласкар (февраль 1997 г.). «О долгосрочной эволюции вращения Земли». Астрономия и астрофизика. 318: 975–989. Bibcode:1997A & A ... 318..975N.
  12. ^ а б Bailer-Jones, C.A.L .; Рыбиски, Дж; Andrae, R .; Фуэнно, М. (2018). «Новые встречи со звездами обнаружены во втором выпуске данных Gaia». Астрономия и астрофизика. 616: A37. arXiv:1805.07581. Bibcode:2018A & A ... 616A..37B. Дои:10.1051/0004-6361/201833456.
  13. ^ Доджсон, Линдси (8 января 2017 г.). «Звезда мчится к нашей Солнечной системе и может сбить миллионы комет прямо к Земле». Business Insider.
  14. ^ Стабильна ли солнечная система? В архиве 2008-06-25 на Wayback Machine
  15. ^ «Планеты Солнечной системы могут выйти из-под контроля». научный сотрудник. Получено 2009-06-11.
  16. ^ Дж. Ласкар; М. Гастино (2009). «Существование траекторий столкновения Меркурия, Марса и Венеры с Землей». Природа. 459 (7248): 817–819. Bibcode:2009Натура.459..817L. Дои:10.1038 / природа08096. PMID  19516336.
  17. ^ Батыгин, Константин (2008). «О динамической устойчивости Солнечной системы». Астрофизический журнал. 683 (2): 1207–1216. arXiv:0804.1946. Bibcode:2008ApJ ... 683.1207B. Дои:10.1086/589232.
  18. ^ Хранилище ванильных долгосрочных интеграций Солнечной системы, 2020, arXiv:2012.05177

внешняя ссылка