Спин-эхо - Spin echo
В магнитный резонанс, а спин-эхо это переориентация вращение намагничивание импульсом резонансного электромагнитное излучение.[1] Современное ядерный магнитный резонанс (ЯМР) и магнитно-резонансная томография (МРТ) используют этот эффект.
В Сигнал ЯМР наблюдаемый после начального импульса возбуждения, затухает со временем из-за как спиновых расслабление и любой неоднородный эффекты, которые вызывают различные вращения в образце прецессия по разным ставкам. Первый из них, релаксация, приводит к необратимой потере намагниченности. Однако неоднородную дефазировку можно устранить, применив угол 180 °. инверсия импульс, инвертирующий векторы намагниченности.[2] Примеры неоднородных эффектов включают градиент магнитного поля и распределение химические сдвиги. Если импульс инверсии применяется после периода т дефазирования, неоднородная эволюция изменится по фазе, чтобы сформировать эхо во время 2т. В простых случаях интенсивность эха относительно исходного сигнала определяется выражением е–2т / т2 куда Т2 - постоянная времени спин-спиновой релаксации. В время эха (TE) - время между импульсом возбуждения и пиком сигнала.[3]
Эхо-явления - важные особенности когерентного спектроскопия которые использовались в полях, отличных от магнитного резонанса, включая лазерная спектроскопия[4] и рассеяние нейтронов. Эхо было впервые обнаружено в ядерном магнитном резонансе Эрвин Хан в 1950 г.[5] и спиновые эхо иногда называют Хан вторит. В ядерный магнитный резонанс и магнитно-резонансная томография, радиочастота наиболее часто используется радиация.
В 1972 г. Ф. Мезей представили спин-эхо-рассеяние нейтронов, метод, который можно использовать для изучения магнонов и фононов в монокристаллах.[6] В настоящее время этот метод применяется в исследовательских центрах с использованием трехосевых спектрометров.
В 2020 году две команды продемонстрировали [7][8] что при сильном связывании ансамбля спинов с резонатором последовательность импульсов Хана приводит не только к одному эхо, но, скорее, к целой серии периодических эхо. В этом процессе первое эхо Хана действует обратно на спины как перефокусирующий импульс, приводя к самостимулируемым вторичным эхо.
Принцип
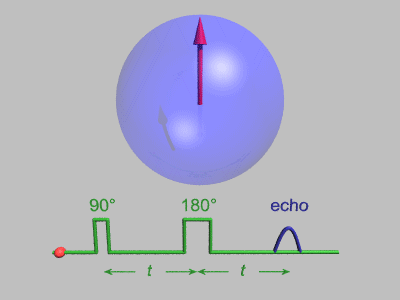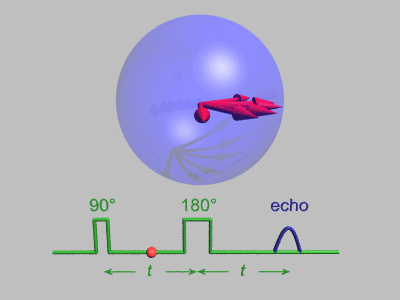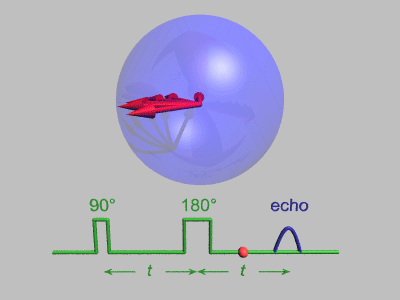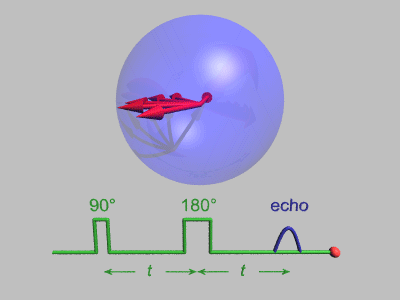
Эффект спинового эха был открыт Эрвин Хан когда он применил два последовательных импульса под углом 90 °, разделенных коротким периодом времени, но обнаружил сигнал, эхо, когда импульс не подавался. Это явление спинового эха было объяснено Эрвином Ханом в его статье 1950 года:[5] и далее развито Карр и Перселл который указал на преимущества использования перефокусирующего импульса 180 ° для второго импульса.[9] Последовательность импульсов можно лучше понять, разбив ее на следующие этапы:
 | |
|
|
В этой последовательности используются несколько упрощений: нет декогеренция включен, и каждое вращение испытывает идеальные импульсы, во время которых окружающая среда не распространяется. Выше показаны шесть спинов, и они не имеют возможности существенно сдвинуть фазу. Техника спинового эха более полезна, когда вращение сдвинуто по фазе более значительно, как показано на анимации ниже:
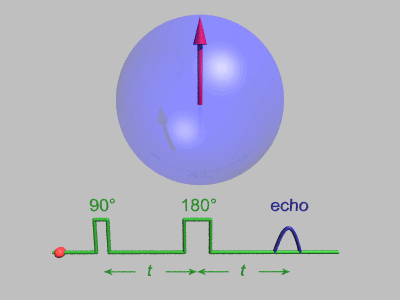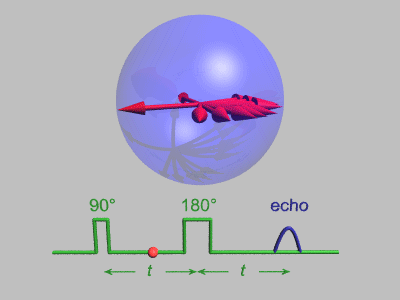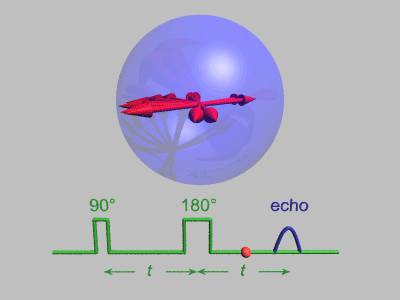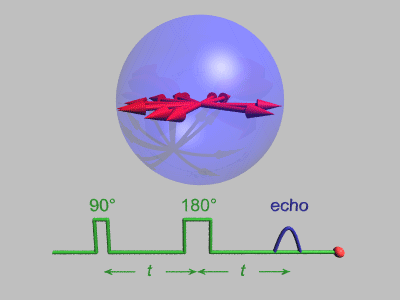
Затухание спинового эха
Эксперимент по затуханию эха Хана может быть использован для измерения спин-спиновая релаксация время, как показано на анимации ниже. Размер эхо-сигнала записывается для разных интервалов между двумя импульсами. Это показывает декогеренцию, которая не перефокусируется π-импульсом. В простых случаях экспоненциальный спад измеряется, что описывается T2 время.

Стимулированное эхо
Бумага Хана 1950 года[5] показали, что еще один метод генерации спинового эха состоит в применении трех последовательных импульсов под углом 90 °. После первого 90-градусного импульса вектор намагниченности расширяется, как описано выше, образуя то, что можно представить как «блин» в плоскости x-y. Распространение продолжается какое-то время , а затем применяется второй импульс 90 °, так что «блин» теперь находится в плоскости x-z. Через некоторое время применяется третий импульс, и через некоторое время наблюдается стимулированное эхо. после последнего пульса.
Фотонное эхо
Эхо Хана также наблюдалось на оптических частотах.[4] Для этого на материал с неоднородно расширенный резонанс поглощения. Вместо использования двух спиновых состояний в магнитном поле, фотонное эхо использует два энергетических уровня, которые присутствуют в материале даже в нулевом магнитном поле.
Смотрите также
- Ядерный магнитный резонанс
- Магнитно-резонансная томография
- Нейтронное спиновое эхо
- Электронный парамагнитный резонанс
Рекомендации
- ^ Дж. Э. Таннер и Э. О. Стейскал (2003). «Ограниченная самодиффузия протонов в коллоидных системах методом импульсного градиента, спин-эхо». Журнал химической физики. 49 (4): 1768. Bibcode:1968ЖЧФ..49.1768Т. Дои:10.1063/1.1670306.
- ^ Малькольм Х. Левитт; Рэй Фриман (1979). «ЯМР-инверсия населенности с использованием составного импульса». Журнал магнитного резонанса. 33 (2): 473–476. Bibcode:1979JMagR..33..473L. Дои:10.1016/0022-2364(79)90265-8.
- ^ Дэн Дж. Белл и Дж. Юнг. «Эхо время». Радиопедия. Получено 2017-09-24.
- ^ а б Kurnit, N.A .; Abella, I.D .; Хартманн, С. Р. (1964). «Наблюдение фотонного эха». Письма с физическими проверками. 13 (19): 567–568. Bibcode:1964ПхРвЛ..13..567К. Дои:10.1103 / PhysRevLett.13.567.
- ^ а б c Хан, Э. (1950). «Спиновое эхо». Физический обзор. 80 (4): 580–594. Bibcode:1950PhRv ... 80..580H. Дои:10.1103 / PhysRev.80.580.
- ^ Mezei, F. (1972), "Нейтронное спиновое эхо: новая концепция в методах поляризованных тепловых нейтронов", Zeitschrift für Physik, 255(2), стр. 146–160.
- ^ Вайксельбаумер, Стефан; Дзенс, Матиас; Zollitsch, Christoph W .; Brandt, Martin S .; Роттер, Стефан; Гросс, Рудольф; Хюбль, Ханс (2020). «Эхо-цуги в импульсном электронном спиновом резонансе сильносвязанного спинового ансамбля». Письма с физическими проверками. 125: 137701. Дои:10.1103 / PhysRevLett.125.137701.
- ^ Дебнат, Каманасиш; Долд, Дэвид; Мортон, Джон Дж. Л .; Мёльмер, Клаус (2020). "Самостимулированные импульсные эхо-цепи от неоднородно уширенных спиновых ансамблей". Письма с физическими проверками. 125: 137702. Дои:10.1103 / PhysRevLett.125.137702.
- ^ Carr, H. Y .; Перселл, Э. М. (1954). "Влияние диффузии на свободную прецессию в экспериментах по ядерному магнитному резонансу". Физический обзор. 94 (3): 630–638. Bibcode:1954PhRv ... 94..630C. Дои:10.1103 / PhysRev.94.630.
дальнейшее чтение
- Рэй Фриман (1999). Хореография вращения: основные этапы ЯМР высокого разрешения. Издательство Оксфордского университета. ISBN 978-0-19-850481-8.
- Малькольм Х. Левитт (2001). Спиновая динамика: основы ядерного магнитного резонанса. Вайли. ISBN 978-0-471-48922-1.
- Артур Швайгер; Гуннар Йешке (2001). Принципы импульсного электронного парамагнитного резонанса. Издательство Оксфордского университета. ISBN 978-0-19-850634-8.
внешняя ссылка
- Анимации и симуляции


