Формула вращения Родригеса - Rodrigues rotation formula

В теории трехмерное вращение, Формула вращения Родригеса, названный в честь Олинде Родригес, является эффективным алгоритмом поворота вектор в космосе, учитывая ось и угол поворота. В дальнейшем это может быть использовано для преобразования всех трех базисные векторы вычислить матрица вращения в $ТАК (3)$ , группа всех матриц вращения, из ось-угол представление. Другими словами, формула Родригеса предоставляет алгоритм для вычисления экспоненциальная карта из $так (3)$ , то Алгебра Ли из $ТАК (3)$ , к $ТАК (3)$ без фактического вычисления полной матричной экспоненты.

Заявление

Если $v$ вектор в $ℝ 3$ и $k$ это единичный вектор описывающая ось вращения, вокруг которой $v$ поворачивается на угол $θ$ согласно правило правой руки, формула Родригеса для повернутого вектора $v гнить$ является

${ displaystyle mathbf {v} _ { mathrm {rot}} = mathbf {v} cos theta + ( mathbf {k} times mathbf {v}) sin theta + mathbf {k } ~ ( mathbf {k} cdot mathbf {v}) (1- cos theta) ,.}$

Альтернативным утверждением является запись вектора оси как перекрестное произведение $а \times б$ любых двух ненулевых векторов $а$ и $б$ которые определяют плоскость вращения, и смысл угла $θ$ измеряется от $а$ и к $б$ . Сдача $α$ обозначают угол между этими векторами, два угла $θ$ и $α$ не обязательно равны, но измеряются в одном и том же смысле. Тогда вектор единичной оси можно записать

{ displaystyle mathbf {k} = { frac { mathbf {a} times mathbf {b}} {| mathbf {a} times mathbf {b} |}} = { frac { mathbf {a} times mathbf {b}} {| mathbf {a} || mathbf {b} | sin alpha}} ,.}

Эта форма может быть более полезной, когда задействованы два вектора, определяющие плоскость. Примером в физике является Прецессия Томаса который включает вращение, заданное формулой Родригеса, с точки зрения двух неколлинеарных скоростей наддува, а ось вращения перпендикулярна их плоскости.

Вывод

Формула вращения Родригеса вращается

v

под углом

θ

вокруг вектора

k

разложив его на составляющие параллельно и перпендикулярно

k

, и вращая только перпендикулярный компонент.

Векторная геометрия формулы вращения Родригеса, а также разложение на параллельную и перпендикулярную составляющие.

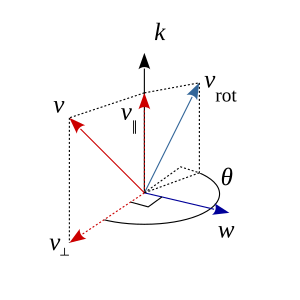
Позволять $k$ быть единичный вектор определяя ось вращения, и пусть $v$ быть любым вектором, чтобы вращаться вокруг $k$ по углу $θ$ (правило правой руки, против часовой стрелки на рисунке).

С использованием точка и перекрестные продукты, вектор $v$ можно разложить на составляющие, параллельные и перпендикулярные оси $k$ ,

{ Displaystyle mathbf {v} = mathbf {v} _ { parallel} + mathbf {v} _ { perp} ,,}

где компонент, параллельный $k$ является

{ Displaystyle mathbf {v} _ { parallel} = ( mathbf {v} cdot mathbf {k}) mathbf {k}}

называется векторная проекция из $v$ на $k$ , а составляющая, перпендикулярная к $k$ является

{ displaystyle mathbf {v} _ { perp} = mathbf {v} - mathbf {v} _ { parallel} = mathbf {v} - ( mathbf {k} cdot mathbf {v} ) mathbf {k} = - mathbf {k} times ( mathbf {k} times mathbf {v})}

называется вектор отклонения из $v$ из $k$ .

Вектор $k \times v$ можно рассматривать как копию $v ⊥$ повернут против часовой стрелки на 90 ° примерно $k$ , поэтому их величины равны, но направления перпендикулярны. Аналогично вектор $k \times (k \times v)$ копия $v ⊥$ повернут против часовой стрелки через $180°$ о $k$ , так что $k \times (k \times v)$ и $v ⊥$ равны по величине, но в противоположных направлениях (т. е. они противоположны друг другу, отсюда знак минус). Расширение вектор тройное произведение устанавливает связь между параллельными и перпендикулярными компонентами, для справки формула: $а \times (б \times c) = (а \cdot c) б - (а \cdot б) c$ учитывая любые три вектора $а$ , $б$ , $c$ .

Компонент, параллельный оси, не изменит ни величину, ни направление при вращении,

{ Displaystyle mathbf {v} _ { parallel mathrm {rot}} = mathbf {v} _ { parallel} ,,}

только перпендикулярный компонент изменит направление, но сохранит свою величину, согласно

{ Displaystyle { begin {align} left | mathbf {v} _ { perp mathrm {rot}} right | & = left | mathbf {v} _ { perp} right | , , mathbf {v} _ { perp mathrm {rot}} & = cos theta mathbf {v} _ { perp} + sin theta mathbf {k} times mathbf {v } _ { perp} ,, end {выровнено}}}

и с тех пор $k$ и $v ∥$ параллельны, их перекрестное произведение равно нулю $k \times v ∥ = 0$ , так что

{ displaystyle mathbf {k} times mathbf {v} _ { perp} = mathbf {k} times left ( mathbf {v} - mathbf {v} _ { parallel} right) = mathbf {k} times mathbf {v} - mathbf {k} times mathbf {v} _ { parallel} = mathbf {k} times mathbf {v}}

и это следует

{ displaystyle mathbf {v} _ { perp mathrm {rot}} = cos theta mathbf {v} _ { perp} + sin theta mathbf {k} times mathbf {v} ,.}

Этот поворот правильный, поскольку векторы $v ⊥$ и $k \times v$ иметь одинаковую длину, и $k \times v$ является $v ⊥$ повернут против часовой стрелки через $90°$ о $k$ . Соответствующее масштабирование $v ⊥$ и $k \times v$ с использованием тригонометрические функции синус и косинус дает повернутую перпендикулярную составляющую. Форма повернутого компонента аналогична радиальному вектору в двухмерной плоской полярные координаты $(р, θ)$ в Декартова основа

{ displaystyle mathbf {r} = r cos theta mathbf {e} _ {x} + r sin theta mathbf {e} _ {y} ,,}

куда $е Икс$ , $е у$ находятся единичные векторы в указанных направлениях.

Теперь полный повернутый вектор

{ displaystyle mathbf {v} _ { mathrm {rot}} = mathbf {v} _ { parallel mathrm {rot}} + mathbf {v} _ { perp mathrm {rot}} , ,}

Подставляя определения $v ∥rot$ и $v ⊥rot$ в уравнении приводит к

{ Displaystyle { begin {align} mathbf {v} _ { mathrm {rot}} & = mathbf {v} _ { parallel} + cos theta , mathbf {v} _ { perp } + sin theta , mathbf {k} times mathbf {v} & = mathbf {v} _ { parallel} + cos theta left ( mathbf {v} - mathbf {v} _ { parallel} right) + sin theta , mathbf {k} times mathbf {v} & = cos theta , mathbf {v} + (1- cos theta) mathbf {v} _ { parallel} + sin theta , mathbf {k} times mathbf {v} & = cos theta , mathbf {v} + ( 1- cos theta) ( mathbf {k} cdot mathbf {v}) mathbf {k} + sin theta , mathbf {k} times mathbf {v} end {выровнено} }}

Матричные обозначения

Представляя $v$ и $k \times v$ в качестве матрицы столбцов, перекрестное произведение может быть выражено как матричный продукт

{ displaystyle { begin {bmatrix} ( mathbf {k} times mathbf {v}) _ {x} ( mathbf {k} times mathbf {v}) _ {y} ( mathbf {k} times mathbf {v}) _ {z} end {bmatrix}} = { begin {bmatrix} k_ {y} v_ {z} -k_ {z} v_ {y} k_ {z} v_ {x} -k_ {x} v_ {z} k_ {x} v_ {y} -k_ {y} v_ {x} end {bmatrix}} = { begin {bmatrix} 0 & - k_ {z} & k_ {y} k_ {z} & 0 & -k_ {x} - k_ {y} & k_ {x} & 0 end {bmatrix}} { begin {bmatrix} v_ {x} v_ {y} v_ {z} end {bmatrix}} ,.}

Сдача $K$ обозначают "матрица перекрестных продуктов "для единичного вектора $k$ ,

{ displaystyle mathbf {K} = left [{ begin {array} {ccc} 0 & -k_ {z} & k_ {y} k_ {z} & 0 & -k_ {x} - k_ {y} & k_ {x} & 0 end {array}} right] ,,}

матричное уравнение, символически,

{ Displaystyle mathbf {K} mathbf {v} = mathbf {k} times mathbf {v}}

для любого вектора $v$ . (Фактически, $K$ - единственная матрица с этим свойством. Он имеет собственные значения 0 и $\pm я$ ).

Итерация поперечного произведения справа эквивалентна умножению на матрицу поперечного произведения слева, в частности

{ Displaystyle mathbf {K} ( mathbf {K} mathbf {v}) = mathbf {K} ^ {2} mathbf {v} = mathbf {k} times ( mathbf {k} раз mathbf {v}) ,.}

Более того, поскольку $k$ - единичный вектор, $K$ есть единица 2-норма. Таким образом, предыдущая формула поворота на матричном языке выглядит так:

{ Displaystyle mathbf {v} _ { mathrm {rot}} = mathbf {v} + ( sin theta) mathbf {K} mathbf {v} + (1- cos theta) mathbf {K} ^ {2} mathbf {v} ,, quad | mathbf {K} | _ {2} = 1 ,.}

Обратите внимание, что коэффициент перед первым членом равен сейчас же 1 в этих обозначениях: см. Обсуждение группы Ли ниже.

Факторизация $v$ позволяет компактное выражение

{ displaystyle { begin {align} mathbf {v} _ { mathrm {rot}} & = mathbf {R} mathbf {v} end {align}}}

куда

${ Displaystyle mathbf {R} = mathbf {I} + ( sin theta) mathbf {K} + (1- cos theta) mathbf {K} ^ {2}}$

это матрица вращения под углом $θ$ против часовой стрелки вокруг оси $k$ , и $я$ то 3 × 3 единичная матрица. Эта матрица $р$ является элементом группы вращения $ТАК (3)$ из $ℝ 3$ , и $K$ является элементом Алгебра Ли ${ displaystyle { mathfrak {so}} (3)}$ порождая эту группу Ли (обратите внимание, что $K$ кососимметрична, что характеризует ${ displaystyle { mathfrak {so}} (3)}$ ).

В терминах матричной экспоненты

{ Displaystyle mathbf {R} = ехр ( theta mathbf {K}) ,.}

Чтобы убедиться, что последняя идентичность сохраняется, нужно отметить, что

{ Displaystyle mathbf {R} ( theta) mathbf {R} ( phi) = mathbf {R} ( theta + phi), quad mathbf {R} (0) = mathbf {I } ,,}

характеристика однопараметрическая подгруппа, т.е. экспоненциальный, и что формулы совпадают для бесконечно малых $θ$ .

Для альтернативного вывода, основанного на этой экспоненциальной зависимости, см. экспоненциальная карта из ${ displaystyle { mathfrak {so}} (3)}$ к $ТАК (3)$ . Об обратном отображении см. карта журнала из $ТАК (3)$ к ${ displaystyle { mathfrak {so}} (3)}$ .

Обратите внимание, что Ходж Дуал вращения ${ displaystyle mathbf {R}}$ просто ${ Displaystyle mathbf {R} ^ {*} = - sin ( theta) mathbf {k}}$ который позволяет извлечь как ось вращения, так и синус угла поворота из самого поворота с обычной неоднозначностью:

{ Displaystyle грех ( тета) = сигма | mathbf {R} ^ {*} |}

{ displaystyle mathbf {k} = - sigma mathbf {R} ^ {*} / | mathbf {R} ^ {*} |}

куда ${ displaystyle sigma = pm 1}$ . Приведенное выше простое выражение является результатом того факта, что двойственный по Ходжу к ${ displaystyle mathbf {I}}$ и ${ displaystyle mathbf {K} ^ {2}}$ равны нулю, а ${ Displaystyle mathbf {K} ^ {*} = - mathbf {k}}$ .