Расслабленный перекресток - Relaxed intersection

В расслабленное пересечение из м множества соответствует классическому пересечению между множествами, за исключением того, что разрешено ослабить несколько множеств, чтобы избежать пустого пересечения. Это понятие можно использовать для решения Ограничивает проблемы удовлетворенности которые несовместимы ослабление небольшого количества ограничений.Когда подход с ограниченной ошибкой рассматривается для оценка параметров, расслабленное пересечение позволяет быть робастным относительно некоторых выбросы.

Определение

В q-расслабленное пересечение м подмножества${\displaystyle X_{1},\dots ,X_{m}}$из ${\displaystyle R^{n}}$, обозначаемый${\displaystyle X^{\{q\}}=\bigcap ^{\{q\}}X_{i}}$это набор всех${\displaystyle x\in R^{n}}$которые принадлежат всем${\displaystyle X_{i}}$, кроме${\displaystyle q}$Это определение показано на рисунке 1.

Рисунок 1. q-пересечение 6 сетов для q= 2 (красный), q= 3 (зеленый), q= 4 (синий), q= 5 (желтый).

Определять${\displaystyle \lambda (x)={\text{card}}\left\{i\ |\ x\in X_{i}\right\}.}$

У нас есть${\displaystyle X^{\{q\}}=\lambda ^{-1}([m-q,m]).}$

Таким образом, характеристика q-релаксированного пересечения установить инверсию проблема.^[1]

Пример

Рассмотрим 8 интервалов:${\displaystyle X_{1}=[1,4],}$${\displaystyle X_{2}=\ [2,4],}$${\displaystyle X_{3}=[2,7],}$${\displaystyle X_{4}=[6,9],}$${\displaystyle X_{5}=[3,4],}$${\displaystyle X_{6}=[3,7].}$

У нас есть

${\displaystyle X^{\{0\}}=\emptyset ,}$${\displaystyle X^{\{1\}}=[3,4],}$${\displaystyle X^{\{2\}}=[3,4],}$${\displaystyle X^{\{3\}}=[2,4]\cup [6,7],}$${\displaystyle X^{\{4\}}=[2,7],}$${\displaystyle X^{\{5\}}=[1,9],}$${\displaystyle X^{\{6\}}=]-\infty ,\infty [.}$

Расслабленное пересечение интервалов

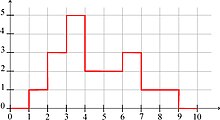
Расслабленное пересечение интервалов не обязательно интервал. Таким образом, мы берем интервальную оболочку результата. Если ${\displaystyle X_{i}}$'s являются интервалами, ослабленное пересечение может быть вычислено со сложностью м.бревно(м) с помощью Алгоритм Марзулло. Достаточно отсортировать все нижние и верхние границы м интервалы для представления функции ${\displaystyle \lambda }$. Тогда легко получаем набор

${\displaystyle X^{\{q\}}=\lambda ^{-1}([m-q,m])}$

что соответствует объединению интервалов. Затем мы возвращаем наименьший интервал, который содержит это объединение.

На рисунке 2 показана функция${\displaystyle \lambda (x)}$связанный с предыдущим примером.

Рисунок 2. Функция принадлежности к множеству, связанная с 6 интервалами.

Расслабленное пересечение ящиков

Чтобы вычислить q-расслабленное пересечение м коробки${\displaystyle R^{n}}$, мы проектируем все м коробки в отношении п осей.Для каждой из п группы м интервалов, мы вычисляем q-расслабленное пересечение. Возвращаем декартово произведение п результирующие интервалы.^[2]На рис. 3 представлена ​​иллюстрация пересечения 6 прямоугольников в расслабленном состоянии. Каждая точка красного квадрата принадлежит 4 из 6 квадратов.

Рисунок 3. Красный прямоугольник соответствует 4-ослабленному пересечению 6 прямоугольников.

Расслабленный союз

В q-расслабленный союз ${\displaystyle X_{1},\dots ,X_{m}}$ определяется

${\displaystyle {\overset {\{q\}}{\bigcup }}X_{i}=\bigcap ^{\{m-1-q\}}X_{i}}$

Обратите внимание, что когда q= 0, расслабленное объединение / пересечение соответствует классическому объединению / пересечению. Точнее, у нас есть

${\displaystyle \bigcap ^{\{0\}}X_{i}=\bigcap X_{i}}$

и

${\displaystyle {\overset {\{0\}}{\bigcup }}X_{i}=\bigcup X_{i}}$

Закон де Моргана

Если ${\displaystyle {\overline {X}}}$ обозначает дополнительный набор ${\displaystyle X_{i}}$, у нас есть

${\displaystyle {\overline {\bigcap ^{\{q\}}X_{i}}}={\overset {\{q\}}{\bigcup }}{\overline {X_{i}}}}$

${\displaystyle {\overline {{\overset {\{q\}}{\bigcup }}X_{i}}}=\bigcap ^{\{q\}}{\overline {X_{i}}}.}$

Как следствие

${\displaystyle {\overline {\bigcap \limits ^{\{q\}}X_{i}}}={\overline {{\overset {\{m-q-1\}}{\bigcup }}X_{i}}}=\bigcap ^{\{m-q-1\}}{\overline {X_{i}}}}$

Расслабление подрядчиков

Позволять ${\displaystyle C_{1},\dots ,C_{m}}$ быть м подрядчики для наборов ${\displaystyle X_{1},\dots ,X_{m}}$,тогда

${\displaystyle C([x])=\bigcap ^{\{q\}}C_{i}([x]).}$

является подрядчиком для ${\displaystyle X^{\{q\}}}$и

${\displaystyle {\overline {C}}([x])=\bigcap ^{\{m-q-1\}}{\overline {C}}_{i}([x])}$

является подрядчиком для ${\displaystyle {\overline {X}}^{\{q\}}}$, куда

${\displaystyle {\overline {C}}_{1},\dots ,{\overline {C}}_{m}}$

являются подрядчиками для

${\displaystyle {\overline {X}}_{1},\dots ,{\overline {X}}_{m}.}$

В сочетании с разветвленный алгоритм, такой как SIVIA (Установить инверсию с помощью интервального анализа), q-расслабленное пересечение м подмножества ${\displaystyle R^{n}}$ можно вычислить.

Приложение к оценке ограниченной ошибки

В q-расслабленное пересечение может использоваться для надежной локализации^[3][4]или для отслеживания.^[5]

Надежные наблюдатели также могут быть реализованы с использованием ослабленных пересечений, чтобы быть устойчивыми по отношению к выбросам.^[6]

Предлагаем здесь простой пример^[7]чтобы проиллюстрировать метод. Рассмотрим модель я-я модель, выход которой представлен

${\displaystyle f_{i}(p)={\frac {1}{\sqrt {2\pi p_{2}}}}\exp(-{\frac {(t_{i}-p_{1})^{2}}{2p_{2}}})}$

куда ${\displaystyle p\in R^{2}}$. Предположим, что мы имеем

${\displaystyle f_{i}(p)\in [y_{i}]}$

куда ${\displaystyle t_{i}}$ и ${\displaystyle [y_{i}]}$ приведены в следующем списке

${\displaystyle \{(1,[0;0.2]),(2,[0.3;2]),(3,[0.3;2]),(4,[0.1;0.2]),(5,[0.4;2]),(6,[-1;0.1])\}}$

Наборы ${\displaystyle \lambda ^{-1}(q)}$ для разных ${\displaystyle q}$ изображены на рисунке 4.

Рисунок 4. Набор всех векторов параметров, соответствующих ровно 6-q столбцам данных (окрашенным красным) для q = 1,2,3,4,5.

Рекомендации

1. Jaulin, L .; Walter, E .; Дидрит, О. (1996). Гарантированное устойчивое нелинейное ограничение параметров (PDF). В материалах конференции CESA'96 IMACS Multiconference (симпозиум по моделированию, анализу и моделированию).
2. Jaulin, L .; Уолтер, Э. (2002). «Гарантированная робастная нелинейная минимаксная оценка» (PDF). IEEE Transactions по автоматическому контролю. 47.
3. Kieffer, M .; Уолтер, Э. (2013). Гарантированная характеристика точных неасимптотических доверительных областей при нелинейном оценивании параметров (PDF). В материалах симпозиума МФБ по нелинейным системам управления, Тулуза: Франция (2013).
4. Drevelle, V .; Боннифайт, доктор наук (2011). «Подход с набором членства для высоконадежного спутникового позиционирования с помощью высоты». Решения GPS. 15 (4).
5. Langerwisch, M .; Вагнер, Б. (2012). «Гарантированное слежение за мобильным роботом с использованием надежного распространения интервальных ограничений». Интеллектуальная робототехника и приложения..
6. Жаулин, Л. (2009). «Оценка состояния членства в робастном множестве; применение в подводной робототехнике» (PDF). Automatica. 45: 202–206. Дои:10.1016 / j.automatica.2008.06.013.
7. Jaulin, L .; Kieffer, M .; Walter, E .; Мейзель, Д. (2002). «Гарантированная робастная нелинейная оценка с приложением к локализации роботов» (PDF). IEEE Transactions по системам, человеку и кибернетике; Часть C Приложения и обзоры. 32. Архивировано из оригинал (PDF) 28 апреля 2011 г.