Алгоритм Марзуллоса - Marzullos algorithm

Алгоритм Марзулло, изобретенный Кейт Марзулло для его доктора философии. диссертация 1984 г., является алгоритм согласования используется для выбора источников для оценки точного времени из ряда шумный источники времени. Усовершенствованная версия, переименованная в "алгоритм пересечения ", является частью современного Сетевой протокол времени Алгоритм Марзулло также используется для вычисления расслабленное пересечение из n коробок (или в более общем смысле п подмножества рп), как того требуют несколько оценка робастного множества методы.

Цель

Алгоритм Марзулло эффективен с точки зрения времени для получения оптимального значения из набора оценок с доверительные интервалы где фактическое значение может выходить за пределы доверительного интервала для некоторых источников. В этом случае наилучшей оценкой считается наименьший интервал последовательный с наибольшим количеством источников.

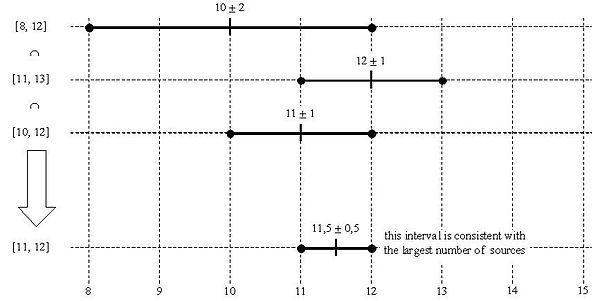
Если у нас есть оценки 10 ± 2, 12 ± 1 и 11 ± 1, то этими интервалами являются [8,12], [11,13] и [10,12], которые пересекаются, образуя [11,12] или 11,5 ± 0,5. соответствует всем трем ценностям.

Алгоритм Марзулло, пример # 1


Если вместо этого диапазоны равны [8,12], [11,13] и [14,15], то нет интервала, согласованного со всеми этими значениями, но [11,12] согласуется с наибольшим числом источников, а именно с двумя их.

Алгоритм Марзулло, пример # 2


Наконец, если диапазоны равны [8,9], [8,12] и [10,12], то оба интервала [8,9] и [10,12] соответствуют наибольшему количеству источников.

Алгоритм Марзулло, пример # 3


Эта процедура определяет интервал. Если желаемый результат представляет собой наилучшее значение из этого интервала, тогда наивный подход будет заключаться в том, чтобы взять центр интервала в качестве значения, что и было указано в исходном алгоритме Марзулло. Более сложный подход предполагает признание того, что это может отбрасывать полезную информацию из доверительных интервалов источников и что вероятностная модель источников может возвращать значение, отличное от центра.

Обратите внимание, что вычисленное значение, вероятно, лучше описать как «оптимистичное», чем «оптимальное». Например, рассмотрим три интервала [10,12], [11, 13] и [11,99,13]. Описанный ниже алгоритм вычисляет [11,99, 12] или 11,995 ± 0,005, что является очень точным значением. Если мы подозреваем, что одна из оценок может быть неверной, то как минимум две оценки должны быть верными. При этом условии наилучшей оценкой является [11,13], поскольку это наибольший интервал, который всегда пересекает по крайней мере две оценки. Описанный ниже алгоритм легко параметризуется максимальным количеством неверных оценок.

Метод

Алгоритм Марзулло начинается с подготовки таблицы источников, ее сортировки и последующего поиска (эффективного) пересечения интервалов. Для каждого источника существует диапазон [c − r, c + r], определяемый как c ± r. Для каждого диапазона в таблице будет два кортежи вида <смещение, тип>. Один кортеж будет представлять начало диапазона, помеченного типом -1 как , а другой будет представлять конец с типом +1 как .

В описании алгоритма используются следующие переменные: best (наибольшее число найденных перекрывающихся интервалов), cnt (текущее число перекрывающихся интервалов), beststart и bestend (начало и конец наилучшего найденного интервала), i (индекс) , и таблица кортежей.

  2. Создайте таблицу кортежей.
  3. Сортировать таблица по смещению. (Если существуют два кортежа с одинаковым смещением, но противоположных типов, что указывает на то, что один интервал заканчивается так же, как начинается другой, тогда необходим метод определения того, какой из них наступит первым. Такое вхождение можно рассматривать как перекрытие без продолжительности, которое можно найти алгоритмом, поместив тип -1 перед типом +1. Если такие патологические совпадения считаются нежелательными, их можно избежать, поставив тип +1 перед -1 в этом случае.)
  4. [инициализировать] best = 0 cnt = 0
  5. [loop] просмотреть каждый кортеж в таблице в порядке возрастания
  2. [текущее количество перекрывающихся интервалов] cnt = cnt-type [i]
  3. если cnt> best then best = cnt beststart = offset [i] bestend = offset [i + 1]
комментарий: следующий кортеж в [i + 1] будет либо концом интервала (type = + 1), и в этом случае он заканчивает этот лучший интервал, либо он будет началом интервала (type = −1 ) и на следующем шаге заменит best.
двусмысленность: не указано, что делать, если best = cnt. Это условие стяжки для наибольшего перекрытия. Решение может быть либо принято, чтобы взять меньшее из bestend-beststart и offset [i + 1] -offset [i], либо просто взять произвольный один из двух одинаково хороших записей. Это решение актуально только при типе [i + 1] = + 1.
  2. [конец цикла] возвращает [beststart, bestend] как оптимальный интервал. Количество ложный sources (те, которые не перекрывают возвращаемый оптимальный интервал) - это количество источников за вычетом значения best.

Эффективность

Алгоритм Марзулло эффективен как в пространстве, так и во времени. В асимптотический использование пространства На), где n - количество источников. При рассмотрении требований к асимптотике времени алгоритм можно рассматривать как состоящий из построения таблицы, ее сортировки и поиска. Сортировка может быть выполнена за O (n log n) времени, и это доминирует на этапах построения и поиска, которые могут выполняться за линейный время. Следовательно, временная эффективность алгоритма Марзулло равна O (п войти п).

После того, как таблица построена и отсортирована, можно обновлять интервал для одного источника (при получении новой информации) в линейное время. Следовательно, обновление данных для одного источника и поиск наилучшего интервала можно выполнить за O (n) время.

Рекомендации

  • Марзулло, К. А. (февраль 1984 г.). «Поддержание времени в распределенной системе: пример слабосвязанной распределенной службы». Кандидат наук. диссертация. Кафедра электротехники. Стэндфордский Университет. КАК В  B000710CSC. OCLC  38621764. ДДК 3781.1984 М.

внешняя ссылка