Прямоугольная маска с кратковременным преобразованием Фурье - Rectangular mask short-time Fourier transform

В математике прямоугольная маска кратковременное преобразование Фурье имеет простую форму кратковременное преобразование Фурье. Для других типов STFT может потребоваться больше времени вычислений, чем для rec-STFT. Определите его функцию маски.

${\displaystyle w(t)={\begin{cases}\ 1;&|t|\leq B\\\ 0;&|t|>B\end{cases}}}$

B = 50, Икс-ось (сек)

Мы можем изменить B для разного сигнала.

Rec-STFT

${\displaystyle X(t,f)=\int _{t-B}^{t+B}x(\tau )e^{-j2\pi f\tau }\,d\tau }$

Обратная форма

${\displaystyle x(t)=\int _{-\infty }^{\infty }X(t_{1},f)e^{j2\pi ft}\,df{\text{ where }}t-B<t_{1}<t+B}$

Свойство

Rec-STFT имеет аналогичные свойства с преобразованием Фурье

• Интеграция

(а)

${\displaystyle \int _{-\infty }^{\infty }X(t,f)\,df=\int _{t-B}^{t+B}x(\tau )\int _{-\infty }^{\infty }e^{-j2\pi f\tau }\,df\,d\tau =\int _{t-B}^{t+B}x(\tau )\delta (\tau )\,d\tau ={\begin{cases}\ x(0);&|t|<B\\\ 0;&{\text{otherwise}}\end{cases}}}$

(б)

${\displaystyle \int _{-\infty }^{\infty }X(t,f)e^{-j2\pi fv}\,df={\begin{cases}\ x(v);&v-B<t<v+B\\\ 0;&{\text{otherwise}}\end{cases}}}$

• Свойство смещения (сдвиг по оси x)

${\displaystyle \int _{t-B}^{t+B}x(\tau +\tau _{0})e^{-j2\pi f\tau }\,d\tau =X(t+\tau _{0},f)e^{j2\pi f\tau _{0}}}$

• Свойство модуляции (сдвиг по у-ось)

${\displaystyle \int _{t-B}^{t+B}[x(\tau )e^{j2\pi f_{0}\tau }]d\tau =X(t,f-f_{0})}$

• специальный ввод

1. Когда ${\displaystyle x(t)=\delta (t),X(t,f)={\begin{cases}\ 1;&|t|<B\\\ 0;&{\text{otherwise}}\end{cases}}}$
2. Когда ${\displaystyle x(t)=1,X(t,f)=2B\operatorname {sinc} (2Bf)e^{j2\pi ft}}$

• Свойство линейности

Если ${\displaystyle h(t)=\alpha x(t)+\beta y(t)\,}$,${\displaystyle H(t,f),X(t,f),}$и ${\displaystyle Y(t,f)\,}$являются их rec-STFT, то

${\displaystyle H(t,f)=\alpha X(t,f)+\beta Y(t,f).}$

• Свойство интеграции мощности

${\displaystyle \int _{-\infty }^{\infty }|X(t,f)|^{2}\,df=\int _{t-B}^{t+B}|x(\tau )|^{2}\,d\tau }$

${\displaystyle \int _{-\infty }^{\infty }\int _{-\infty }^{\infty }|X(t,f)|^{2}\,df\,dt=2B\int _{-\infty }^{\infty }|x(\tau )|^{2}\,d\tau }$

• Свойство суммы энергии (Теорема Парсеваля )

${\displaystyle \int _{-\infty }^{\infty }X(t,f)Y^{*}(t,f)\,df=\int _{t-B}^{t+B}x(\tau )y^{*}(\tau )\,d\tau }$

${\displaystyle \int _{-\infty }^{\infty }\int _{-\infty }^{\infty }X(t,f)Y^{*}(t,f)\,df\,dt=2B\int _{-\infty }^{\infty }x(\tau )y^{*}(\tau )\,d\tau }$

Прямоугольная маска Bэффект

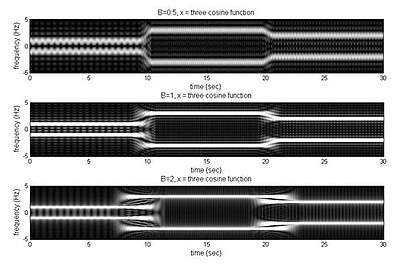
сравнение различных B

Из изображения, когда B чем меньше, тем лучше временное разрешение. В противном случае, когда B чем больше, тем лучше разрешение по частоте.

Мы можем выбрать указанные B для определения разрешения по времени и по частоте.

Преимущества и недостатки

• Сравните с преобразованием Фурье

ПреимуществоМожно наблюдать мгновенную частоту.

НедостатокБолее высокая сложность вычислений.

• По сравнению с другими типами частотно-временного анализа:

Rec-STFT имеет преимущество наименьшего времени вычислений для цифровой реализации, но его производительность хуже, чем у других типов частотно-временного анализа.

Смотрите также

• Принцип неопределенности

Рекомендации

1. Jian-Jiun Ding (2014) Частотно-временной анализ и вейвлет-преобразование