Рациональное движение - Rational motion

В кинематика, движение жесткое тело определяется как непрерывный набор перемещений. Однопараметрические движения можно определить как непрерывное перемещение движущегося объекта относительно фиксированной системы отсчета в трехмерном евклидовом пространстве (E³), где смещение зависит от одного параметра, чаще всего определяемого как время.

Рациональные движения определены рациональные функции (соотношение двух полиномиальные функции ) времени. Они производят рациональные траектории, и поэтому они хорошо интегрируются с существующими NURBS (Non-Uniform Rational B-Spline) на основе отраслевого стандарта CAD / CAM системы. Они легко поддаются применению существующих компьютерный геометрический дизайн (CAGD) алгоритмы. Объединив кинематику движений твердого тела с геометрией NURBS кривые и поверхности, разработаны методы для системы автоматизированного проектирования рациональных движений.

Эти методы САПР для проектирования движения находят применение в анимация в компьютерной графике (ключевой кадр интерполяция ), планирование траектории в робототехника (интерполяция позиции обучения), пространственная навигация в виртуальная реальность, компьютерное геометрическое моделирование движения с помощью интерактивной интерполяции, ЧПУ планирование траектории инструмента, и спецификацию задачи в синтез механизма.

Фон

Было проведено множество исследований по применению принципов автоматизированного геометрического проектирования (CAGD) к проблеме автоматизированного проектирования движений. В последние годы было хорошо установлено, что рациональный Безье и рациональный B-шлиц схемы представления кривых можно комбинировать с двойной кватернион представление ^[1] из пространственные перемещения для получения рациональных движений Безье и B-сплайнов. Ге и Равани,^[2][3] разработал новую основу для геометрических построений пространственных движений, объединив концепции кинематики и CAGD. Их работа была построена на основополагающей статье Шумейка,^[4] в котором он использовал понятие кватернион ^[5] за вращение интерполяция. Подробный список литературы по этой теме можно найти в ^[6] и.^[7]

Рациональные движения Безье и B-сплайны

Позволять ${displaystyle {hat { extbf {q}}}={ extbf {q}}+varepsilon { extbf {q}}^{0}}$обозначают единичный двойственный кватернион. Однородный дуальный кватернион можно записать как пару кватернионов, ${displaystyle {hat { extbf {Q}}}={ extbf {Q}}+varepsilon { extbf {Q}}^{0}}$; куда ${displaystyle { extbf {Q}}=w{ extbf {q}},{ extbf {Q}}^{0}=w{ extbf {q}}^{0}+w^{0}{ extbf {q}}}$. Это достигается за счет расширения ${displaystyle {hat { extbf {Q}}}={hat {w}}{hat { extbf {q}}}}$ с помощьюдвойной номер алгебра (здесь, ${displaystyle {hat {w}}=w+varepsilon w^{0}}$).

В терминах двойных кватернионов и однородные координаты точки ${displaystyle { extbf {P}}:(P_{1},P_{2},P_{3},P_{4})}$ объекта уравнение преобразования кватернионов имеет вид

${displaystyle { ilde { extbf {P}}}={ extbf {Q}}{ extbf {P}}{ extbf {Q}}^{ast }+P_{4}[({ extbf {Q}}^{0}){ extbf {Q}}^{ast }-{ extbf {Q}}({ extbf {Q}}^{0})^{ast }],}$куда ${displaystyle { extbf {Q}}^{ast }}$ и ${displaystyle ({ extbf {Q}}^{0})^{ast }}$ являются конъюгатами ${displaystyle { extbf {Q}}}$ и ${displaystyle { extbf {Q}}^{0}}$соответственно и${displaystyle { ilde { extbf {P}}}}$ обозначает однородные координаты точки после смещения.^[7]

Учитывая набор единичных двойных кватернионов и двойных весов ${displaystyle {hat { extbf {q}}}_{i},{hat {w}}_{i};i=0...n}$ соответственно, следующее представляет собой рациональную кривую Безье в пространстве двойных кватернионов.

${displaystyle {hat { extbf {Q}}}(t)=sum limits _{i=0}^{n}{B_{i}^{n}(t){hat { extbf {Q}}}_{i}}=sum limits _{i=0}^{n}{B_{i}^{n}(t){hat {w}}_{i}{hat { extbf {q}}}_{i}}}$

куда ${displaystyle B_{i}^{n}(t)}$ - многочлены Бернштейна. Двойственная кватернионная кривая Безье, заданная уравнением выше, определяет рациональное движение Безье степени ${displaystyle 2n}$.

Точно так же двойная кватернионная кривая B-сплайна, которая определяет NURBS-движение степени 2п, дан кем-то,

${displaystyle {hat { extbf {Q}}}(t)=sum limits _{i=0}^{n}{N_{i,p}(t){hat { extbf {Q}}}_{i}}=sum limits _{i=0}^{n}{N_{i,p}(t){hat {w}}_{i}{hat { extbf {q}}}_{i}}}$

куда ${displaystyle N_{i,p}(t)}$ являются пБазисные функции B-сплайна й степени.

Представление для рационального движения Безье и рационального движения B-сплайна в декартовом пространстве может быть получено путем замены любого из двух предыдущих выражений для ${displaystyle {hat { extbf {Q}}}(t)}$ в уравнении точечного преобразования. В дальнейшем мы будем иметь дело со случаем рационального движения Безье. Траектория точки, совершающей рациональное движение Безье, задается формулой

${displaystyle { ilde { extbf {P}}}^{2n}(t)=[H^{2n}(t)]{ extbf {P}},}$

${displaystyle H^{2n}(t)]=sum limits _{k=0}^{2n}{B_{k}^{2n}(t)[H_{k}]},}$

куда ${displaystyle [H^{2n}(t)]}$ - матричное представление рационального движения Безье степени${displaystyle 2n}$ в декартовом пространстве. Следующие матрицы${displaystyle [H_{k}]}$ (также называемые контрольными матрицами Безье) определяют аффинная управляющая структура движения:

${displaystyle [H_{k}]={frac {1}{C_{k}^{2n}}}sum limits _{i+j=k}{C_{i}^{n}C_{j}^{n}w_{i}w_{j}[H_{ij}^{ast }]},}$

куда ${displaystyle [H_{ij}^{ast }]=[H_{i}^{+}][H_{j}^{-}]+[H_{j}^{-}][H_{i}^{0+}]-[H_{i}^{+}][H_{j}^{0-}]+(alpha _{i}-alpha _{j})[H_{j}^{-}][Q_{i}^{+}]}$.

В приведенных выше уравнениях ${displaystyle C_{i}^{n}}$ и ${displaystyle C_{j}^{n}}$- биномиальные коэффициенты и ${displaystyle alpha _{i}=w_{i}^{0}/w_{i},alpha _{j}=w_{j}^{0}/w_{j}}$ весовые отношения и

${displaystyle [H_{j}^{-}]=left[{egin{array}{rrrr}q_{j,4}&-q_{j,3}&q_{j,2}&-q_{j,1}q_{j,3}&q_{j,4}&-q_{j,1}&-q_{j,2}-q_{j,2}&q_{j,1}&q_{j,4}&-q_{j,3}q_{j,1}&q_{j,2}&q_{j,3}&q_{j,4}end{array}}ight],}$

${displaystyle [Q_{i}^{+}]=left[{egin{array}{rrrr}0&0&0&q_{i,1}�&0&0&q_{i,2}�&0&0&q_{i,3}�&0&0&q_{i,4}end{array}}ight],}$

${displaystyle [H_{i}^{0+}]=left[{egin{array}{rrrr}0&0&0&q_{i,1}^{0}�&0&0&q_{i,2}^{0}�&0&0&q_{i,3}^{0}�&0&0&q_{i,4}^{0}end{array}}ight],}$

${displaystyle [H_{j}^{0-}]=left[{egin{array}{rrrr}0&0&0&-q_{j,1}^{0}�&0&0&-q_{j,2}^{0}�&0&0&-q_{j,3}^{0}�&0&0&q_{j,4}^{0}end{array}}ight],}$

${displaystyle [H_{i}^{+}]=left[{egin{array}{rrrr}q_{i,4}&-q_{i,3}&q_{i,2}&q_{i,1}q_{i,3}&q_{i,4}&-q_{i,1}&q_{i,2}-q_{i,2}&q_{i,1}&q_{i,4}&q_{i,3}-q_{i,1}&-q_{i,2}&-q_{i,3}&q_{i,4}end{array}}ight].}$

В приведенных выше матрицах ${displaystyle (q_{i,1},q_{i,2},q_{i,3},q_{i,4})}$четыре компонента реальной части ${displaystyle ({ extbf {q}}_{i})}$ и${displaystyle (q_{i,1}^{0},q_{i,2}^{0},q_{i,3}^{0},q_{i,4}^{0})}$ четыре компонента двойной части${displaystyle ({ extbf {q}}_{i}^{0})}$ двойного кватерниона ${displaystyle ({hat { extbf {q}}}_{i})}$.

Пример

Чайник с рациональным движением Безье степени 6 с (слева) единичными действительными весами (${displaystyle {hat {w}}_{i}=1+epsilon 0;i=0..3}$) (справа) неединичные действительные веса (${displaystyle {hat {w}}_{i}=1+epsilon 0;i=0,3}$ и ${displaystyle {hat {w}}_{i}=4+epsilon 0;i=1,2}$); также показаны аффинные позиции (искаженные), а также заданные контрольные позиции (синим цветом).

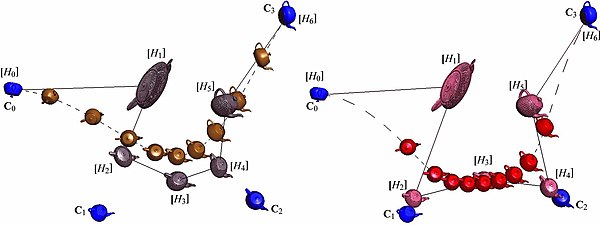
Смотрите также

• Кватернион и Двойной кватернион
• NURBS
• Компьютерная анимация
• Робототехника
• Кинематика робота
• Вычислительная геометрия
• ЧПУ механическая обработка
• Конструкция механизма

Рекомендации

1. Маккарти, Дж. М. (1990). Введение в теоретическую кинематику. MIT Press, Кембридж, Массачусетс, США. ISBN  978-0-262-13252-7.
2. Ge, Q.J .; Равани, Б. (1994). «Компьютерный геометрический дизайн движущихся интерполянтов». Журнал механического проектирования. 116 (3): 756–762. Дои:10.1115/1.2919447.
3. Ge, Q.J .; Равани, Б. (1994). «Геометрическое построение движений Безье». Журнал механического проектирования. 116 (3): 749–755. Дои:10.1115/1.2919446.
4. Shoemake, К. (1985). «Анимация вращения с кватернионными кривыми». Материалы 12-й ежегодной конференции по компьютерной графике и интерактивным технологиям. 19 (3): 245–254. Дои:10.1145/325334.325242. ISBN  978-0897911665.
5. Bottema, O .; Рот, Б. (1990). Теоретическая кинематика (Теоретическая кинематика). Dover Publications. ISBN  978-0-486-66346-3.
6. Рёшель, О. (1998). «Рациональный моушн-дизайн - обзор». Системы автоматизированного проектирования. 30 (3): 169–178. Дои:10.1016 / S0010-4485 (97) 00056-0.
7. Purwar, A .; Ге, К. Дж. (2005). «О влиянии двойных гирь на компьютерное проектирование рациональных движений». Журнал механического проектирования. 127 (5): 967–972. Дои:10.1115/1.1906263.

внешняя ссылка

• Лаборатория кинематики вычислительного проектирования
• Лаборатория робототехники и пространственных систем (РАССЛ)
• Лаборатория робототехники и автоматизации