Перспективность - Perspectivity

Для более широкого освещения этой темы см. Аксонометрия).

В геометрия и в своих приложениях к Рисование, а перспективность формирование образа в картина самолет сцены, просматриваемой с фиксированной точки.

Графика

Наука о графическая перспектива использует перспективность для создания реалистичных изображений с правильными пропорциями. В соответствии с Кирсти Андерсен, первым автором, описавшим перспективность, был Леон Альберти в его De Pictura (1435).^[1] По-английски, Брук Тейлор представил свой Линейная перспектива в 1715 г., где он объяснил: «Перспектива - это искусство рисования на плоскости любых фигур по правилам геометрии».^[2] Во второй книге Новые принципы линейной перспективы (1719), писал Тейлор

Когда линии, проведенные в соответствии с определенным законом из нескольких частей любой фигуры, разрезают плоскость и этим разрезанием или пересечением описывают фигуру на этой плоскости, эта фигура, описанная таким образом, называется Проекция другого рисунка. Линии, производящие эту проекцию, вместе взятые, называются Система лучей. И когда все эти Лучи проходят через одну и ту же Точку, их называют Конус лучей. И когда эта Точка рассматривается как Глаз наблюдателя, эта Система Лучей называется Оптический конус^[3]

Проективная геометрия

Перспективность:
${\displaystyle ABCD\doublebarwedge A'B'C'D',}$

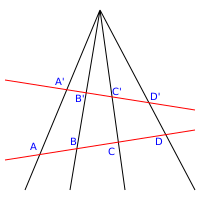
В проективная геометрия точки линии называются проективный диапазон, а набор прямых на плоскости на точке называется карандаш.

Учитывая два линии ${\displaystyle \ell }$ и ${\displaystyle m}$ в самолет и точка п этого самолета ни на одной линии, биективное отображение между точками диапазона ${\displaystyle \ell }$ и диапазон ${\displaystyle m}$ определяется линиями карандаша на п называется перспективность (а точнее, центральная перспектива с центром п).^[4] Чтобы показать, что точки Икс и Y связаны перспективностью; ${\displaystyle X\doublebarwedge Y.}$ В этих обозначениях, чтобы показать, что центр перспективы п, записывать ${\displaystyle X\ {\overset {P}{\doublebarwedge }}\ Y.}$

Наличие перспективности означает, что соответствующие точки находятся в перспектива. В двойной концепция, осевая перспективность, есть соответствие между линиями двух пучков, определяемое проективным образом.

Проективность

Основная статья: Проективность

Сочетание двух перспектив - это вообще не перспектива. Перспективность или сочетание двух или более перспектив называется проективность (проективное преобразование, проективная коллинеация и омография находятся синонимы ).

Есть несколько результатов, касающихся проекций и перспектив, которые справедливы в любом паппиан проективная плоскость:^[5]

Теорема: любую проективность между двумя различными проективными диапазонами можно записать как композицию не более чем двух перспектив.

Теорема: любая проективность от проективного диапазона к самой себе может быть записана как композиция трех перспектив.

Теорема: проективность между двумя различными проективными диапазонами, которая фиксирует точку, является перспективностью.

Многомерные перспективы

Биективное соответствие между точками на двух прямых на плоскости, определяемой точкой этой плоскости, не лежащей ни на одной прямой, имеет многомерные аналоги, которые также будут называться перспективностями.

Позволять S_м и Т_м быть двумя разными м-мерные проективные пространства, содержащиеся в п-мерное проективное пространство р_п. Позволять п_п−м−1 быть (п − м - 1) -мерное подпространство р_п не имеющий общих точек ни с одним S_м или же Т_м. Для каждой точки Икс из S_м, космос L охватывает Икс и п_п-м-1 встречает Т_м в точке Y = ж_п(Икс). Эта переписка ж_п также называется перспективностью.^[6] Описанная выше центральная перспектива относится к п = 2 и м = 1.

Перспективные коллинеации

Позволять S₂ и Т₂ - две различные проективные плоскости в проективном 3-пространстве р₃. С О и О* будучи точками р₃ ни в одной из плоскостей, используйте конструкцию последней секции для проецирования S₂ на Т₂ перспективностью с центром О сопровождаемый проекцией Т₂ обратно на S₂ с перспективой с центром О*. Эта композиция представляет собой биективная карта пунктов S₂ на себя, который сохраняет коллинеарен точек и называется коллинеация перспективы (центральная коллинеация в более современной терминологии).^[7] Пусть φ - перспективная коллинеация S₂. Каждая точка линии пересечения S₂ и Т₂ будет фиксироваться на φ, и эта прямая называется ось из φ. Пусть точка п быть пересечением линии OO* с самолетом S₂. п также фиксируется φ, и каждая линия S₂ что проходит через п стабилизируется по φ (фиксировано, но не обязательно поточечно фиксировано). п называется центр из φ. Ограничение φ на любую линию S₂ не проходя через п центральная перспектива в S₂ с центром п между этой линией и линией, которая является его изображением под φ.

Смотрите также

• Перспективная проекция

Примечания

Жан Дю Брёй, Diverses methods universelles et nouvelles, en tout ou en partie pour faire des перспективах, 1642

1. Кирсти Андерсен (2007) Геометрия искусства, страница 1, Springer ISBN  978-0-387-25961-1
2. Андерсен 1992, п. 75
3. Андерсен 1992, п. 163
4. Кокстер 1969, п. 242
5. Fishback 1969, стр. 65–66
6. Педое 1988, стр. 282–3
7. Молодой 1930, п. 116

Рекомендации

• Андерсен, Кирсти (1992), Работа Брука Тейлора о линейной перспективе, Спрингер, ISBN  0-387-97486-5
• Коксетер, Гарольд Скотт Макдональд (1969), Введение в геометрию (2-е изд.), Нью-Йорк: Джон Уайли и сыновья, ISBN  978-0-471-50458-0, МИСТЕР  0123930
• Фишбэк, W.T. (1969), Проективная и евклидова геометрия, Джон Уайли и сыновья
• Педое, Дэн (1988), Геометрия / Комплексный курс, Дувр, ISBN  0-486-65812-0
• Янг, Джон Уэсли (1930), Проективная геометрия, The Carus Mathematical Monographs (# 4), Математическая ассоциация Америки

внешняя ссылка

• Кристофер Купер Перспективы и перспективы.
• Джеймс К. Морхед младший (1911) Перспективная и проективная геометрии: сравнение из Университет Райса.
• Джон Тейлор Проективная геометрия из Университет Брайтона.