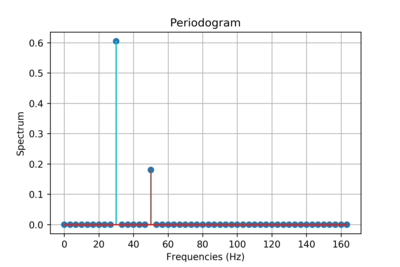
Периодограмма - Periodogram

В обработка сигналов, а периодограмма это оценка спектральная плотность сигнала. Термин был придуман Артур Шустер в 1898 г.^[1] Сегодня периодограмма является составной частью более сложных методов (см. спектральная оценка ). Это наиболее распространенный инструмент для исследования амплитудных и частотных характеристик КИХ-фильтры и оконные функции. Анализаторы спектра БПФ также реализованы как временная последовательность периодограмм.

Определение

Сегодня используются как минимум два разных определения^[2]. Один из них предполагает усреднение по времени,^[3] а один нет.^[4] Усреднение по времени также входит в компетенцию других статей (Метод Бартлетта и Метод Велча ). Эта статья не об усреднении по времени. Интересующее здесь определение состоит в том, что спектральная плотность мощности непрерывной функции ${\displaystyle x(t),}$ это преобразование Фурье функции автокорреляции (см. Теорема взаимной корреляции ):

${\displaystyle {\mathcal {F}}\{x(t)\ast x(-t)\}=X(f)\cdot X^{*}(f)=\left|X(f)\right|^{2}.}$

Вычисление

Спектр мощности (возведенный в квадрат) двух синусоидальных базисных функций, вычисленный методом периодограммы.

Два спектра мощности (квадрат величины) (прямоугольный и Хэмминговский оконные функции плюс фоновый шум), рассчитанный методом периодограммы.

При достаточно малых значениях параметра Т, произвольно точное приближение для Икс(ж) можно наблюдать в регионе${\displaystyle -{\tfrac {1}{2T}}<f<{\tfrac {1}{2T}}}$ функции:

${\displaystyle X_{1/T}(f)\ {\stackrel {\text{def}}{=}}\ \sum _{k=-\infty }^{\infty }X\left(f-k/T\right),}$

что точно определяется по образцам Икс(нТл) которые охватывают ненулевую продолжительность Икс(т) (видеть Дискретное преобразование Фурье ).

И при достаточно больших значениях параметра N,  ${\displaystyle X_{1/T}(f)}$ может быть оценено на сколь угодно близкой частоте путем суммирования формы:

${\displaystyle X_{1/T}\left({\tfrac {k}{NT}}\right)=\sum _{n=-\infty }^{\infty }\underbrace {T\cdot x(nT)} _{x[n]}\cdot e^{-i2\pi {\frac {kn}{N}}},}$

куда k целое число. Периодичность${\displaystyle e^{-i2\pi {\frac {kn}{N}}}}$ позволяет очень просто записать это в терминах Дискретное преобразование Фурье:

${\displaystyle X_{1/T}\left({\tfrac {k}{NT}}\right)=\underbrace {\sum _{n}x_{_{N}}[n]\cdot e^{-i2\pi {\frac {kn}{N}}},} _{DFT}\quad \scriptstyle {{\text{(sum over any }}n{\text{-sequence of length }}N)},}$

куда ${\displaystyle x_{_{N}}}$ представляет собой периодическое суммирование:${\displaystyle x_{_{N}}[n]\ \triangleq \sum _{m=-\infty }^{\infty }x[n-mN].}$

При оценке для всех целых чисел k, от 0 до N-1, массив:

${\displaystyle S\left({\tfrac {k}{NT}}\right)=\left|\sum _{n}x_{_{N}}[n]\cdot e^{-i2\pi {\frac {kn}{N}}}\right|^{2}}$

это периодограмма.^[4][5][6]

Приложения

Периодограмма для Проксима Центавра b отображается внизу.^[7]

Когда периодограмма используется для изучения подробных характеристик КИХ-фильтр или же оконная функция, параметр N выбирается кратным ненулевой продолжительности Икс[п] последовательность, которая называется заполнение нулями (видеть § Выборка DTFT ).^[A] Когда он используется для реализации банк фильтров, N является несколькими частями ненулевой продолжительности Икс[п] последовательность (см. § Выборка DTFT ).

Одним из недостатков периодограммы является то, что отклонение при заданном частота не уменьшается при увеличении количества выборок, используемых в вычислениях. Он не обеспечивает усреднение, необходимое для анализа шумоподобных сигналов или даже синусоид при низких отношениях сигнал / шум. Оконные функции и импульсные характеристики фильтров бесшумны, но для многих других сигналов требуются более сложные методы спектральная оценка. В двух альтернативных вариантах периодограммы используются как часть процесса:

• В метод усредненных периодограмм,^[8] более известный как Метод Велча,^[9][10] делит длинную последовательность x [n] на несколько более коротких и, возможно, перекрывающихся подпоследовательностей. Он вычисляет оконную периодограмму каждого из них и вычисляет среднее значение массива, то есть массив, в котором каждый элемент представляет собой среднее значение соответствующих элементов всех периодограмм. За стационарные процессы, это уменьшает дисперсию шума каждого элемента примерно на коэффициент, обратный количеству периодограмм.
• Сглаживание это метод усреднения по частоте, а не по времени. Сглаженную периодограмму иногда называют спектральный сюжет.^[11][12]

Методы, основанные на периодограммах, вносят небольшие искажения, которые недопустимы в некоторых приложениях. Другие техники, не основанные на периодограммах, представлены в оценка спектральной плотности статья.

Смотрите также

• Соответствующий фильтр
• Отфильтрованная обратная проекция (Преобразование Радона)
• Метод Велча
• Метод Бартлетта
• Дискретное преобразование Фурье
• Спектральный анализ методом наименьших квадратов, для вычисления периодограмм в данных, которые не равномерно разнесены
• МНОЖЕСТВЕННАЯ СИГНАЛЬНАЯ КЛАССИФИКАЦИЯ (МУЗЫКА), популярный параметрический сверхразрешение метод
• САМВ

Примечания

1. N обозначен NFFT в приложениях Matlab и Octave.

Рекомендации

1. Шустер, Артур (Январь 1898 г.). «Об исследовании скрытых периодичностей применительно к предполагаемому 26-дневному периоду метеорологических явлений» (PDF). Земной магнетизм. 3 (1): 13–41. Bibcode:1898TeMag ... 3 ... 13S. Дои:10.1029 / TM003i001p00013. Удобно иметь слово для некоторого представления переменной величины, которая должна соответствовать «спектру» светового излучения. Предлагаю слово периодограмма, и определим его более конкретно следующим образом.
2. Максуини, Лаура А. (2004-05-14). «Сравнение периодограмм». Журнал статистических вычислений и моделирования. онлайн (50 долларов). 76 (4): 357–369. Дои:10.1080/10629360500107618.
3. «Периодограмма - документация на языке Wolfram Language».
4. «Оценка спектральной плотности мощности периодограммы - периодограмма MATLAB».
5. Оппенгейм, Алан В.; Шафер, Рональд В.; Бак, Джон Р. (1999). Обработка сигналов в дискретном времени (2-е изд.). Верхняя Сэдл-Ривер, штат Нью-Джерси: Prentice Hall. п. 732 (10,55). ISBN  0-13-754920-2. url =https://d1.amobbs.com/bbs_upload782111/files_24/ourdev_523225.pdf
6. Rabiner, Lawrence R .; Золото, Бернард (1975). «6,18». Теория и применение цифровой обработки сигналов. Энглвуд Клиффс, Нью-Джерси: Прентис-Холл. стр.415. ISBN  0-13-914101-4.
7. «Наука своими руками - Проксима c прячется на этом графике?». www.eso.org. Получено 11 сентября 2017.
8. Энгельберг, С. (2008), Цифровая обработка сигналов: экспериментальный подход, Springer, гл. 7 п. 56
9. Уэлч, Питер Д. (июнь 1967). «Использование быстрого преобразования Фурье для оценки спектров мощности: метод, основанный на усреднении по времени по коротким модифицированным периодограммам». IEEE Transactions по аудио и электроакустике. AU-15 (2): 70–73. Bibcode:1967ITAE ... 15 ... 70 Вт. Дои:10.1109 / TAU.1967.1161901.
10. "Оценка спектральной плотности мощности Уэлча - MATLAB pwelch".
11. Спектральный сюжет, от NIST Справочник по инженерной статистике.
12. «Справочное руководство DATAPLOT» (PDF). NIST.gov. Национальный институт стандартов и технологий (NIST). 1997-03-11. Получено 2019-06-14. Спектральный график по сути представляет собой «сглаженную» периодограмму, где сглаживание выполняется в частотной области.

дальнейшее чтение

• Box, George E. P .; Дженкинс, Гвилим М. (1976). Анализ временных рядов: прогнозирование и контроль. Сан-Франциско: Холден-Дэй.
• Скаргл, Дж. Д. (15 декабря 1982 г.). «Исследования по анализу астрономических временных рядов. II - Статистические аспекты спектрального анализа неравномерно распределенных данных». Астрофизический журнал, часть 1. 263: 835–853. Bibcode:1982ApJ ... 263..835S. Дои:10.1086/160554.
• Воан, Саймон; Аттли, Филипп (2006). «Обнаружение рентгеновских QPO в активных галактиках». Успехи в космических исследованиях. 38 (7): 1405–1408. arXiv:astro-ph / 0506456. Bibcode:2006AdSpR..38.1405V. Дои:10.1016 / j.asr.2005.02.064.