График нормальной вероятности - Normal probability plot
В график нормальной вероятности это графическая техника выявить существенные отклонения от нормальность. Это включает определение выбросы, перекос, эксцесс, необходимость преобразований, и смеси. Графики нормальной вероятности состоят из необработанных данных, остатки от соответствия модели, и оценочные параметры.

На графике нормальной вероятности (также называемом «нормальным графиком») отсортированные данные отображаются в зависимости от значений, выбранных так, чтобы полученное изображение выглядело близко к прямой линии, если данные приблизительно нормально распределены. Отклонения от прямой линии предполагают отклонения от нормы. Построение может быть выполнено вручную с помощью специального миллиметровая бумага, называется нормальная вероятностная бумага. На современных компьютерах обычные графики обычно создаются с помощью программного обеспечения.
График нормальной вероятности является частным случаем Q – Q график вероятностей для нормального распределения. Теоретическая квантили обычно выбираются так, чтобы аппроксимировать либо среднее, либо медиану соответствующих статистика заказов.
Определение
График нормальной вероятности формируется путем построения отсортированных данных в зависимости от приближения к средним или медианам соответствующих статистика заказов; видеть рангит. Некоторые пользователи наносят данные на вертикальную ось;[1] другие откладывают данные на горизонтальной оси.[2][3]
В разных источниках используются несколько разные приближения для ранки. Формула, используемая функцией qqnorm в базовом пакете stats в R (язык программирования) как следует:
за я = 1, 2, ..., п, куда
- а = 3/8 если п ≤ 10 и
- 0.5 для п > 10,
и Φ−1 стандартный нормальный квантильная функция.
Если данные согласуются с выборкой из нормального распределения, точки должны лежать близко к прямой линии. В качестве ориентира по точкам можно провести прямую линию. Чем дальше точки отклоняются от этой линии, тем больше указание на отклонение от нормы. Если образец имеет среднее значение 0, стандартное отклонение 1, тогда можно использовать линию, проходящую через 0, с наклоном 1.
Чем больше очков, тем меньше случайные отклонения от линии. Обычные графики часто используются всего с 7 точками, например, при построении эффектов в насыщенной модели из Двухуровневый дробно-факторный эксперимент. Чем меньше баллов, тем труднее отличить случайную изменчивость от существенного отклонения от нормы.
Другие дистрибутивы
Точно так же рассчитываются графики вероятностей для распределений, отличных от нормального. Нормальная функция квантиля Φ−1 просто заменяется функцией квантиля желаемого распределения. Таким образом, можно легко построить график вероятности для любого распределения, для которого имеется функция квантиля.
С семейство распределений в масштабе местоположения, то место расположения и параметры шкалы распределения можно оценить из перехватить и склон линии. Для других распределений параметры должны быть сначала оценены, прежде чем можно будет построить график вероятности.
Типы участков
Это выборка размером 50 из нормального распределения, построенная как в виде гистограммы, так и в виде графика нормальной вероятности.
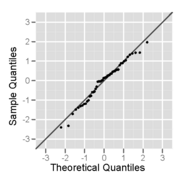
График нормальной вероятности выборки из нормального распределения - он выглядит довольно прямым, по крайней мере, когда игнорируются несколько больших и малых значений.

Гистограмма выборки из нормального распределения - выглядит довольно симметричной и одномодальной
Это выборка размером 50 из распределения со смещением вправо, построенная как в виде гистограммы, так и в виде графика нормальной вероятности.
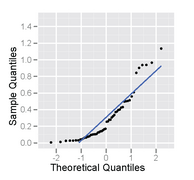
График нормальной вероятности выборки из распределения со смещением вправо - он имеет форму перевернутой C.
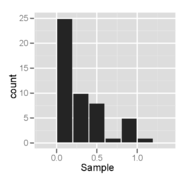
Гистограмма выборки из распределения со смещением вправо - она выглядит одномодальной и смещенной вправо.
Это выборка размером 50 из равномерного распределения, построенная как в виде гистограммы, так и в виде графика нормальной вероятности.
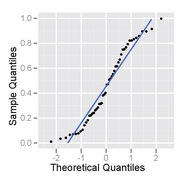
График нормальной вероятности выборки из равномерного распределения - он имеет S-образную форму.

Гистограмма выборки из равномерного распределения - она выглядит мультимодальной и предположительно примерно симметричной.
Смотрите также
Рекомендации
![]() Эта статья включаетматериалы общественного достояния от Национальный институт стандартов и технологий интернет сайт https://www.nist.gov.
Эта статья включаетматериалы общественного достояния от Национальный институт стандартов и технологий интернет сайт https://www.nist.gov.
Эта статья включает Список ссылок, связанное чтение или внешняя ссылка, но его источники остаются неясными, потому что в нем отсутствует встроенные цитаты. (Июль 2011 г.) (Узнайте, как и когда удалить этот шаблон сообщения) |
- ^ например, Chambers et al. (1983, глава 6. Оценка допущений о распределении данных, стр. 194)
- ^ Box, Джордж Э. П.; Дрейпер, Норман (2007), Поверхности отклика, смеси и анализ гребней (2-е изд.), Wiley, ISBN 978-0-470-05357-7
- ^ Titterington, D.M .; Smith, A. F. M .; Маков, У. Э. (1985), "4. Изучение параметров смеси", Статистический анализ распределений конечной смеси, Wiley, ISBN 0-471-90763-4
дальнейшее чтение
- Чемберс, Джон; Уильям Кливленд; Победите Кляйнера; Пол Тьюки (1983). Графические методы анализа данных. Уодсворт.
внешняя ссылка
- Справочник по инженерной статистике: график нормальной вероятности
- Statit Support: Тестирование на «почти нормальность»: график вероятности







