Модель следования за автомобилем Newells - Newells car-following model
Эта статья поднимает множество проблем. Пожалуйста помоги Улучши это или обсудите эти вопросы на страница обсуждения. (Узнайте, как и когда удалить эти сообщения-шаблоны) (Узнайте, как и когда удалить этот шаблон сообщения)
|
В теория транспортного потока, Модель следования за автомобилем Ньюэлла это метод, используемый для определения того, как транспортные средства следуют друг за другом на проезжей части. Основная идея этой модели заключается в том, что транспортное средство будет поддерживать минимальный промежуток времени и пространства между ним и транспортным средством, которое ему предшествует. Таким образом, под перегружен условиях, если ведущий автомобиль изменяет свою скорость, следующий автомобиль также изменит скорость в точке во времени-пространстве вдоль волна движения скорость, -w.[1]
Обзор
Если предположить фундаментальная диаграмма (плотность потока) - треугольная функция, состояние движения А со скоростью vА и плотность kА можно предположить в области скопления. Плотность проезжей части может быть определена с использованием расстояния между транспортными средствами и вычисляется простым уравнением:
kА = 1 / сА
Геометрические отношения из фундаментальная диаграмма также можно использовать для расчета плотности, задаваемой уравнением:
kА = (kj ш)/(vА+ w)
На пространственно-временной диаграмме траектории ведущего (вверху) и следующего (внизу) транспортного средства разделены расстоянием δ и время τ. Расстояние между транспортными средствами в состоянии движения A можно найти с помощью геометрического соотношения, найденного на пространственно-временной диаграмме:
sА = vА(τ)+ δ
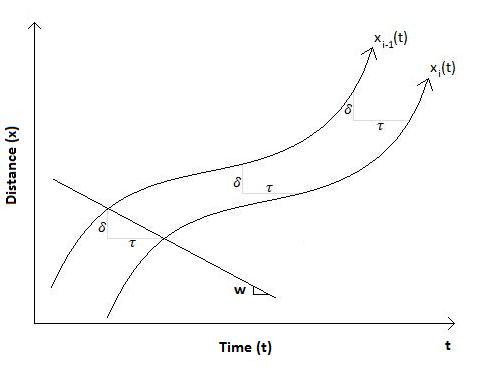
Используя отношения между предыдущими уравнениями, переменные τ и δ можно решить для:
τ = 1/(неделяj)
δ = 1/kj
Таким образом, τ и δ - константы, определяемые скоростью волны и плотностью заторов, не зависящие от скорости ведущего транспортного средства и состояния движения. Путь автомобиля я, функция времени, может быть определена с помощью уравнения:
Икся(т) = мин (ИксАF(т), ИксАC(т))
Положение автомобиля я в безнапорных условиях:
ИксяF(т) = хя(т-т) + vж * τ
Положение автомобиля я в условиях перегруженности:
ИксяC(т) = хя-1(т-т) - δ
Агрессивность водителя
В реальных условиях гипотетический следящий водитель может двигаться неправильно, что приведет к отклонениям от пространственно-временных траекторий, предложенных в модели Ньюэлла. Пространственно-временные траектории из данных, собранных на дорогах и автомагистралях, можно сравнить с траекторией движения соответствующей машины Ньюэлла, чтобы определить, осторожен водитель или агрессивен. На следующих рисунках показаны траектории двух транспортных средств (черные) и траектория, предсказанная моделью следования за автомобилем Ньюэлла для следующего транспортного средства (синий).
Пространственно-временная траектория для нормального водителя:

Пространственно-временная траектория для осторожного водителя:

Пространственно-временная траектория для агрессивного водителя:

Когда следующий водитель реагирует рано при замедлении или поздно реагирует при ускорении, время и расстояние между ведущим и ведомым увеличивается. Последователя можно охарактеризовать как осторожного водителя. В другой ситуации ведомый реагирует позже при замедлении или раньше при ускорении, уменьшая разрыв во времени и расстоянии между ведущим и ведомым. Последователя можно охарактеризовать как агрессивного водителя.
Смотрите также
- Модель Гиппса
- Модель интеллектуального водителя
- Принцип минимизации поломки Кернера
- Теория трехфазного движения
- Моделирование дорожного движения
- Пробки: реконструкция на основе трехфазной теории Кернера
Рекомендации
- ^ Ньюэлл Г.Ф. (2002) Упрощенная теория следования за автомобилем: модель более низкого порядка. Институт транспортных исследований Калифорнийского университета в Беркли.
