Многорукий бандит - Multi-armed bandit

Ряд игровых автоматов в Лас-Вегасе

В теория вероятности, то проблема многорукого бандита (иногда называют K-^[1] или же N-вооруженный бандит проблема^[2]) - это проблема, в которой фиксированный ограниченный набор ресурсов должен быть распределен между конкурирующими (альтернативными) вариантами выбора таким образом, чтобы максимизировать их ожидаемый выигрыш, когда свойства каждого выбора известны только частично во время распределения и могут быть лучше поняты как время идет или распределяя ресурсы по выбору.^[3][4] Это классика обучение с подкреплением проблема, которая иллюстрирует дилемму компромисса между разведкой и эксплуатацией. Название происходит от представления азартный игрок в ряду игровые автоматы (иногда известный как "однорукие бандиты "), который должен решать, на каких машинах играть, сколько раз играть на каждой машине и в каком порядке играть на них, а также продолжать ли играть на текущей машине или пробовать другую.^[5] Проблема многоруких бандитов также попадает в широкую категорию стохастическое планирование.

В задаче каждая машина предоставляет случайную награду из распределение вероятностей специально для этой машины. Цель игрока - максимизировать сумму вознаграждений, заработанных последовательностью нажатий на рычаг.^[3][4] Решающий компромисс, с которым игрок сталкивается в каждом испытании, - это между «эксплуатацией» машины, которая дает наибольший ожидаемый выигрыш, и «исследованием», чтобы получить больше Информация об ожидаемой отдаче от других машин. Компромисс между разведкой и разработкой также встречается в машинное обучение. На практике многорукие бандиты использовались для моделирования таких проблем, как управление исследовательскими проектами в большой организации, такой как научный фонд или фармацевтическая компания.^[3][4] В ранних версиях задачи игрок начинает без начальных знаний об автоматах.

Герберт Роббинс в 1952 г., осознавая важность проблемы, разработал конвергентные стратегии отбора населения в «некоторых аспектах последовательного планирования экспериментов».^[6] Теорема, Индекс Гиттинса, впервые опубликовано Джон С. Гиттинс, дает оптимальную политику для максимизации ожидаемого дисконтированного вознаграждения.^[7]

Эмпирическая мотивация

Как данный бюджет должен быть распределен между этими исследовательскими отделами, чтобы максимизировать результаты?

Проблема многорукого бандита моделирует агента, который одновременно пытается получить новые знания (так называемые «исследования») и оптимизировать свои решения на основе существующих знаний (так называемые «эксплуатация»). Агент пытается сбалансировать эти конкурирующие задачи, чтобы максимизировать их общую ценность за рассматриваемый период времени. Есть много практических применений модели бандита, например:

• клинические испытания изучение эффектов различных экспериментальных методов лечения при минимизации потерь пациентов,^[3][4][8][9]
• адаптивная маршрутизация усилия по минимизации задержек в сети,
• дизайн финансового портфеля^[10][11]

В этих практических примерах проблема требует уравновешивания максимизации вознаграждения на основе уже приобретенных знаний с попытками новых действий для дальнейшего увеличения знаний. Это известно как компромисс между эксплуатацией и разведкой в машинное обучение.

Модель также использовалась для управления динамическим распределением ресурсов по различным проектам, отвечая на вопрос о том, над каким проектом работать, учитывая неопределенность в отношении сложности и окупаемости каждой возможности.^[12]

Первоначально считалось учеными союзников в Вторая Мировая Война, это оказалось настолько трудноразрешимым, что, согласно Питер Уиттл, проблему предлагалось снять Германия так что немецкие ученые тоже могли тратить на это время.^[13]

Часто анализируемая версия проблемы была сформулирована Герберт Роббинс в 1952 г.

Модель многорукого бандита

Многорукий бандит (сокращенно: бандит или МАБ) можно рассматривать как набор реальных распределения ${\displaystyle B=\{R_{1},\dots ,R_{K}\}}$, каждое распределение связано с вознаграждением, предоставленным одним из ${\displaystyle K\in \mathbb {N} ^{+}}$ рычаги. Позволять ${\displaystyle \mu _{1},\dots ,\mu _{K}}$ - средние значения, связанные с этим распределением вознаграждения. Игрок итеративно использует один рычаг за раунд и наблюдает за соответствующей наградой. Цель - максимизировать сумму собранных наград. Горизонт ${\displaystyle H}$ - количество оставшихся раундов. Бандитская проблема формально эквивалентна однозначной Марковский процесс принятия решений. В сожалеть ${\displaystyle \rho }$ после ${\displaystyle T}$ раундов определяется как ожидаемая разница между суммой вознаграждения, связанной с оптимальной стратегией, и суммой собранных вознаграждений:

${\displaystyle \rho =T\mu ^{*}-\sum _{t=1}^{T}{\widehat {r}}_{t}}$,

куда ${\displaystyle \mu ^{*}}$ - среднее значение максимального вознаграждения, ${\displaystyle \mu ^{*}=\max _{k}\{\mu _{k}\}}$, и ${\displaystyle {\widehat {r}}_{t}}$ это награда в раунде т.

А стратегия без сожаления стратегия, в которой среднее сожаление за раунд ${\displaystyle \rho /T}$ стремится к нулю с вероятностью 1, когда количество сыгранных раундов стремится к бесконечности.^[14] Интуитивно понятно, что стратегии нулевого сожаления гарантированно сходятся к (не обязательно уникальной) оптимальной стратегии, если сыграно достаточно раундов.

Вариации

Распространенной формулировкой является Бинарный многорукий бандит или же Многорукий бандит Бернулли, который с вероятностью дает награду в размере одного ${\displaystyle p}$, а в противном случае - ноль.

В другой формулировке многорукого бандита каждая рука представляет собой независимую машину Маркова. Каждый раз, когда играется определенная рука, состояние этой машины переходит к новой, выбранной в соответствии с вероятностями эволюции состояния Маркова. Есть награда в зависимости от текущего состояния машины. В обобщении, называемом «проблемой неугомонного бандита», состояния неиспользованного оружия также могут изменяться со временем.^[15] Также обсуждались системы, в которых количество вариантов выбора (о том, какой рукой играть) увеличивается со временем.^[16]

Исследователи информатики изучали многоруких бандитов при наихудших предположениях, получая алгоритмы, минимизирующие сожаление как в конечном, так и в бесконечном (асимптотический ) временные горизонты для стохастических^[1] и нестохастический^[17] выплаты рук.

Бандитские стратегии

Основным прорывом стало построение оптимальных стратегий или политик отбора населения (которые обладают равномерно максимальной скоростью конвергенции к совокупности с наивысшим средним значением) в работе, описанной ниже.

Оптимальные решения

В статье «Асимптотически эффективные адаптивные правила распределения» Лай и Роббинс^[18] (следуя работам Роббинса и его сотрудников, восходящим к Роббинсу в 1952 году) построили конвергентные политики отбора населения, которые обладают самой быстрой скоростью конвергенции (к населению с наивысшим средним значением) для случая, когда распределение вознаграждения населения является единым. -параметрическое экспоненциальное семейство. Затем в Катехакис и Роббинс^[19] упрощения политики и основные доказательства были даны для случая нормальных популяций с известными дисперсиями. Следующий заметный прогресс был достигнут Burnetas и Катехакис в статье «Оптимальные адаптивные политики для задач последовательного распределения»,^[20] где были построены политики на основе индексов с равномерно максимальной скоростью сходимости при более общих условиях, которые включают случай, когда распределения результатов для каждой группы населения зависят от вектора неизвестных параметров. Бернетас и Катехакис (1996) также предоставили явное решение для важного случая, когда распределения результатов следуют произвольным (т.е. непараметрическим) дискретным одномерным распределениям.

Позже в «Оптимальных адаптивных политиках для марковских процессов принятия решений»^[21] Бёрнетас и Катехакис изучили гораздо более крупную модель марковских процессов принятия решений при частичной информации, где переходный закон и / или ожидаемое вознаграждение за один период могут зависеть от неизвестных параметров. В этой работе явная форма для класса адаптивных политик, которые обладают свойствами равномерно максимальной скорости сходимости для общего ожидаемого вознаграждения за конечный горизонт, была построена при достаточных предположениях о конечных пространствах состояний и неприводимости закона перехода. Главная особенность этих политик заключается в том, что выбор действий для каждого состояния и периода времени основан на показателях, которые представляют собой инфляцию правой части уравнений оптимальности расчетного среднего вознаграждения. Эти инфляции недавно были названы оптимистическим подходом в работах Тевари и Бартлетта:^[22] Ортнер^[23] Филиппи, Каппе и Гаривье,^[24] и Хонда и Такемура.^[25]

Когда оптимальные решения многоруких бандитских задач ^[26] используются для определения ценности выбора животных, активность нейронов миндалины и вентрального полосатого тела кодирует значения, полученные на основе этих политик, и может использоваться для декодирования, когда животные делают исследовательский выбор, а не эксплуататорский. Более того, оптимальные стратегии лучше предсказывают поведение выбора животных, чем альтернативные стратегии (описанные ниже). Это говорит о том, что оптимальные решения проблем многоруких бандитов являются биологически правдоподобными, несмотря на то, что они требуют больших вычислительных ресурсов. ^[27]

• UCBC (исторические верхние границы доверия с кластерами): ^[28] Алгоритм адаптирует UCB для новых настроек, так что он может включать как кластеризацию, так и историческую информацию. Алгоритм включает исторические наблюдения за счет использования как при вычислении наблюдаемых средних вознаграждений, так и члена неопределенности. Алгоритм включает информацию о кластеризации, играя на двух уровнях: сначала выбирая кластер, используя UCB-подобную стратегию на каждом временном шаге, а затем выбирая руку в кластере, снова используя UCB-подобную стратегию.

Примерные решения

Существует множество стратегий, которые обеспечивают приблизительное решение проблемы бандитов, и их можно разделить на четыре основные категории, подробно описанные ниже.

Полуоднородные стратегии

Полуоднородные стратегии были самыми ранними (и простейшими) стратегиями, открытыми для приближенного решения проблемы бандитов. Все эти стратегии объединяет жадный поведение, когда Лучший рычаг (на основе предыдущих наблюдений) всегда тянется, кроме случаев, когда выполняется (равномерно) случайное действие.

• Эпсилон-жадная стратегия:^[29] Подбирается лучший рычаг для пропорции ${\displaystyle 1-\epsilon }$ испытаний, и рычаг выбирается случайным образом (с равномерной вероятностью) для пропорции ${\displaystyle \epsilon }$. Типичное значение параметра может быть ${\displaystyle \epsilon =0.1}$, но это может сильно варьироваться в зависимости от обстоятельств и предпочтений.
• Стратегия первого взгляда на эпсилон^{[нужна цитата ]}: За фазой чистой разведки следует фаза чистой эксплуатации. За ${\displaystyle N}$ испытаний в целом, фаза разведки занимает ${\displaystyle \epsilon N}$ испытания и этап эксплуатации ${\displaystyle (1-\epsilon )N}$ испытания. Во время фазы исследования рычаг выбирается случайным образом (с равномерной вероятностью); на этапе эксплуатации всегда выбирается лучший рычаг.
• Стратегия уменьшения эпсилона^{[нужна цитата ]}: Аналогично стратегии epsilon-greedy, за исключением того, что значение ${\displaystyle \epsilon }$ уменьшается по мере продвижения эксперимента, что приводит к очень исследовательскому поведению в начале и очень эксплуататорскому поведению в конце.
• Адаптивная эпсилон-жадная стратегия, основанная на различиях ценностей (VDBE): Подобно стратегии уменьшения эпсилон, за исключением того, что эпсилон уменьшается на основе прогресса обучения, а не вручную (Tokic, 2010).^[30] Большие колебания в оценках стоимости приводят к высокому эпсилону (высокая разведка, низкая эксплуатация); низкие колебания к низкому эпсилону (низкая разведка, высокая эксплуатация). Дальнейших улучшений можно добиться с помощью softmax -взвешенный отбор действий в случае поисковых действий (Tokic & Palm, 2011).^[31]
• Адаптивная эпсилон-жадная стратегия на основе байесовских ансамблей (Epsilon-BMC): Стратегия адаптивной эпсилон-адаптации для обучения с подкреплением, аналогичная VBDE, с гарантиями монотонной сходимости. В этой структуре параметр эпсилон рассматривается как ожидание апостериорного распределения, взвешивающего жадного агента (который полностью доверяет изученному вознаграждению) и унифицированного обучающего агента (который не доверяет изученному вознаграждению). Это апостериорное значение аппроксимируется с использованием подходящего бета-распределения в предположении нормальности наблюдаемых вознаграждений. Чтобы устранить возможный риск слишком быстрого уменьшения эпсилон, неопределенность в дисперсии полученного вознаграждения также моделируется и обновляется с использованием модели нормальной гаммы. (Гимельфарб и др., 2019).^[32]
• Контекстуально-эпсилон-жадная стратегия: Аналогично стратегии epsilon-greedy, за исключением того, что значение ${\displaystyle \epsilon }$ вычисляется относительно ситуации в экспериментальных процессах, что позволяет алгоритму быть контекстно-зависимым. Он основан на динамическом исследовании / эксплуатации и может адаптивно уравновесить два аспекта, решая, какая ситуация наиболее актуальна для исследования или эксплуатации, что приводит к высокоразвитому поведению, когда ситуация не критическая, и поведению с высокой степенью эксплуатации в критической ситуации.^[33]

Стратегии сопоставления вероятностей

Стратегии сопоставления вероятностей отражают идею о том, что количество нажатий на данный рычаг должно матч его фактическая вероятность быть оптимальным рычагом. Стратегии сопоставления вероятностей также известны как Выборка Томпсона или байесовские бандиты,^[34][35] и их удивительно легко реализовать, если вы можете взять апостериорную выборку для среднего значения каждой альтернативы.

Стратегии сопоставления вероятностей также допускают решения так называемых проблем контекстного бандита.^{[нужна цитата ]}.

Стратегии ценообразования

Стратегии ценообразования устанавливают цена для каждого рычага. Например, как показано на алгоритме POKER,^[14] цена может быть суммой ожидаемого вознаграждения плюс оценка дополнительных будущих вознаграждений, которые будут получены за счет дополнительных знаний. Рычаг наивысшей цены всегда нажат.

Стратегии с этическими ограничениями

• Выборка Томпсона с ограничениями на поведение (BCTS) ^[36]: В этой статье авторы подробно описывают новый онлайн-агент, который изучает набор поведенческих ограничений путем наблюдения и использует эти изученные ограничения в качестве руководства при принятии решений в онлайн-среде, при этом оставаясь реактивным на вознаграждение за обратную связь. Чтобы определить этот агент, было решено принять новое расширение классической контекстной настройки многорукого бандита и предоставить новый алгоритм под названием Behavior Constrained Thompson Sampling (BCTS), который позволяет онлайн-обучение при соблюдении экзогенных ограничений. Агент изучает ограниченную политику, которая реализует наблюдаемые поведенческие ограничения, продемонстрированные агентом учителя, а затем использует эту ограниченную политику для управления онлайн-исследованием и эксплуатацией на основе вознаграждения.

Эти стратегии сводят к минимуму назначение любого пациента в нижнюю руку ("долг врача" ). В типичном случае они минимизируют ожидаемые потерянные успехи (ESL), то есть ожидаемое количество благоприятных исходов, которые были упущены из-за назначения в группу, которая позже оказалась ниже. Другая версия минимизирует потери ресурсов на более низкое и более дорогое лечение.^[8]

Контекстный бандит

Особенно полезной версией многорукого бандита является контекстная проблема многорукого бандита. В этой задаче на каждой итерации агент должен выбирать между руками. Перед тем как сделать выбор, агент видит d-мерный вектор признаков (вектор контекста), связанный с текущей итерацией. Учащийся использует эти векторы контекста вместе с наградами за руки, сыгранные в прошлом, чтобы сделать выбор руки для игры в текущей итерации. Со временем цель обучаемого - собрать достаточно информации о том, как векторы контекста и вознаграждения соотносятся друг с другом, чтобы он мог предсказать следующую лучшую руку для игры, глядя на векторы признаков.^[37]

Примерные решения для контекстного бандита

Существует множество стратегий, которые обеспечивают приблизительное решение проблемы контекстного бандита, и их можно разделить на две большие категории, подробно описанные ниже.

Онлайн линейные бандиты

• LinUCB (Верхняя граница уверенности) алгоритм: авторы предполагают линейную зависимость между ожидаемой наградой за действие и его контекстом и моделируют пространство представления, используя набор линейных предикторов.^[38][39]
• Алгоритм LinRel (линейное ассоциативное обучение с подкреплением): Подобен LinUCB, но использует Разложение по сингулярным числам скорее, чем Регрессия хребта для получения оценки уверенности.^[40][41]
• HLINUCBC (исторический LINUCB с кластерами): предложено в статье ^[42], расширяет идею LinUCB как исторической, так и кластерной информацией.^[43]

Онлайн-нелинейные бандиты

• Алгоритм UCBogram: Нелинейные функции вознаграждения оцениваются с использованием кусочно-постоянной оценки, называемой регрессограмма в непараметрическая регрессия. Затем на каждом постоянном участке используется UCB. Последовательные уточнения раздела контекстного пространства планируются или выбираются адаптивно.^[44][45][46]
• Обобщенные линейные алгоритмы: Распределение вознаграждения следует обобщенной линейной модели, расширенной до линейных бандитов.^{[47][48][49][50]}
• Алгоритм NeuralBandit: В этом алгоритме несколько нейронных сетей обучаются моделировать ценность вознаграждений, зная контекст, и он использует подход с несколькими экспертами для онлайн-выбора параметров многослойных перцептронов.^[51]
• Алгоритм KernelUCB: ядерная нелинейная версия linearUCB с эффективной реализацией и анализом за конечное время.^[52]
• Алгоритм Bandit Forest: а случайный лес строится и анализируется на основе случайного леса, построенного с учетом совместного распределения контекстов и вознаграждений.^[53]
• Алгоритм на основе Oracle: Алгоритм сводит проблему контекстного бандита к серии задач контролируемого обучения и не полагается на типичное предположение о реализуемости функции вознаграждения.^[54]

Сдержанный контекстный бандит

• Контекстные бандиты или контекстные бандиты с ограниченным контекстом ^[55]: Авторы рассматривают новую формулировку модели многорукого бандита, которая называется контекстным бандитом с ограниченным контекстом, в которой учащийся может получить доступ только к ограниченному количеству функций на каждой итерации. Эта новая формулировка мотивирована различными онлайн-проблемами, возникающими в ходе клинических испытаний, систем рекомендаций и моделирования внимания. Здесь они адаптируют стандартный алгоритм многорукого бандита, известный как выборка Томпсона, чтобы воспользоваться преимуществами настройки ограниченного контекста, и предлагают два новых алгоритма, называемых выборкой Томпсона с ограниченным контекстом (TSRC) и выборкой Томпсона Windows с ограниченным контекстом (WTSRC). ), для работы в стационарных и нестационарных средах соответственно.

На практике обычно существует стоимость, связанная с ресурсом, потребляемым каждым действием, а общая стоимость ограничивается бюджетом во многих приложениях, таких как краудсорсинг и клинические испытания. Ограниченный контекстный бандит (CCB) - это такая модель, которая учитывает как временные, так и бюджетные ограничения в условиях многорукого бандита. Badanidiyuru et al.^[56] впервые изучил контекстных бандитов с ограничениями бюджета, также называемых Находчивыми контекстными бандитами, и показал, что ${\displaystyle O({\sqrt {T}})}$ сожаление достижимо. Однако их работа сосредоточена на конечном наборе политик, а алгоритм неэффективен с точки зрения вычислений.

Структура UCB-ALP для ограниченных контекстных бандитов

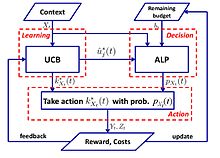
Простой алгоритм с логарифмическим сожалением предлагается в:^[57]

• Алгоритм UCB-ALP: Структура UCB-ALP показана на правом рисунке. UCB-ALP - это простой алгоритм, который объединяет метод UCB с алгоритмом адаптивного линейного программирования (ALP), и его можно легко развернуть в практических системах. Это первая работа, показывающая, как добиться логарифмического сожаления у ограниченных контекстуальных бандитов. Несмотря на то что^[57] посвящен частному случаю с единым бюджетным ограничением и фиксированной стоимостью, результаты проливают свет на разработку и анализ алгоритмов для более общих задач CCB.

Состязательный бандит

Другой вариант проблемы многорукого бандита, названный состязательным бандитом, впервые был предложен Ауэром и Чезой-Бьянки (1998). В этом варианте на каждой итерации агент выбирает руку, а противник одновременно выбирает структуру выигрыша для каждой руки. Это одно из самых сильных обобщений проблемы бандитов.^[58] поскольку он удаляет все предположения о распределении, и решение проблемы состязательных бандитов является обобщенным решением более конкретных проблем бандитов.

Пример: повторяющаяся дилемма заключенного

Примером, часто рассматриваемым в качестве противоборствующих бандитов, является повторяющаяся дилемма заключенного. В этом примере каждый противник должен тянуть две руки. Они могут либо отрицать, либо признаться. Стандартные алгоритмы стохастического бандита не очень хорошо работают с этими итерациями. Например, если противник сотрудничает в первых 100 раундах, дефекты в следующих 200, затем сотрудничают в следующих 300 и т. Д. Тогда такие алгоритмы, как UCB, не смогут очень быстро отреагировать на эти изменения. Это связано с тем, что после определенного момента неоптимальные руки редко используются, чтобы ограничить исследования и сосредоточиться на эксплуатации. Когда окружающая среда изменяется, алгоритм не может адаптироваться или может даже не обнаружить изменение.

Примерные решения

Exp3^[59]

Алгоритм

 Параметры: Настоящий ${\displaystyle \gamma \in (0,1]}$  Инициализация: ${\displaystyle \omega _{i}(1)=1}$ за ${\displaystyle i=1,...,K}$  Для каждого t = 1, 2, ..., T 1. Установить ${\displaystyle p_{i}(t)=(1-\gamma ){\frac {\omega _{i}(t)}{\sum _{j=1}^{K}\omega _{j}(t)}}+{\frac {\gamma }{K}}}$       ${\displaystyle i=1,...,K}$  2. Рисовать ${\displaystyle i_{t}}$ случайно по вероятностям ${\displaystyle p_{1}(t),...,p_{K}(t)}$  3. Получите награду ${\displaystyle x_{i_{t}}(t)\in [0,1]}$  4. Для ${\displaystyle j=1,...,K}$ набор:${\displaystyle {\hat {x}}_{j}(t)={\begin{cases}x_{j}(t)/p_{j}(t)&{\text{if }}j=i_{t}\\0,&{\text{otherwise}}\end{cases}}}$       ${\displaystyle \omega _{j}(t+1)=\omega _{j}(t)exp(\gamma {\hat {x}}_{j}(t)/K)}$

Объяснение

Exp3 с вероятностью случайным образом выбирает руку ${\displaystyle (1-\gamma )}$ он предпочитает руки с более высоким весом (эксплуатировать), он выбирает с вероятностью γ для равномерного случайного исследования. После получения наград веса обновляются. Экспоненциальный рост значительно увеличивает вес хороших рук.

Анализ сожаления

(Внешнее) сожаление алгоритма Exp3 не более${\displaystyle O({\sqrt {KTlog(K)}})}$

Следуйте алгоритму возмущенного лидера (FPL)

Алгоритм

 Параметры: Настоящий ${\displaystyle \eta }$  Инициализация: ${\displaystyle \forall i:R_{i}(1)=0}$  Для каждого t = 1,2, ..., T 1. Для каждого плеча сгенерируйте случайный шум из экспоненциального распределения. ${\displaystyle \forall i:Z_{i}(t)\sim Exp(\eta )}$  2. Потяните за руку ${\displaystyle I(t)}$: ${\displaystyle I(t)=arg\max _{i}\{R_{i}(t)+Z_{i}(t)\}}$     Добавьте шум к каждой руке и потяните за руку с наибольшим значением 3. Обновите значение: ${\displaystyle R_{I(t)}(t+1)=R_{I(t)}(t)+x_{I(t)}(t)}$     Остальное остается прежним

Объяснение

Мы следим за рукой, которая, по нашему мнению, имеет лучшую производительность, добавляя к ней экспоненциальный шум для обеспечения исследования.^[60]

Exp3 против FPL

Exp3	FPL
Поддерживает веса для каждой руки для расчета вероятности вытягивания	Не нужно знать вероятность вытягивания на руку
Имеет эффективные теоретические гарантии	Стандартный FPL не имеет хороших теоретических гарантий
Может быть дорогостоящим с точки зрения вычислений (вычисление экспоненциальных членов)	Вычислительно достаточно эффективный

Бесконечно вооруженный бандит

В исходной спецификации и в вышеупомянутых вариантах проблема бандита задается дискретным и конечным числом рук, часто обозначаемым переменной ${\displaystyle K}$. В случае бесконечного вооружения, введенном Агарвалом (1995), «руки» являются непрерывной переменной в ${\displaystyle K}$ размеры.

Нестационарный бандит

Гаривье и Мулен получили некоторые из первых результатов в отношении проблем бандитов, в которых лежащая в основе модель может изменяться во время игры. Для этого случая был представлен ряд алгоритмов, включая Discounted UCB.^[61] и UCB с раздвижным окном.^[62]

Другая работа Буртини и др. вводит метод взвешенной выборки Томпсона методом наименьших квадратов (WLS-TS), который оказывается полезным как в известных, так и в неизвестных нестационарных случаях.^[63] В известном нестационарном случае авторы в ^[64] выработать альтернативное решение, вариант UCB, названный Скорректированная верхняя граница уверенности (A-UCB), который предполагает стохастическую модель и обеспечивает верхние границы сожаления.

Другие варианты

В последние годы было предложено множество вариантов задачи.

Дуэльный бандит

Вариант дуэльного бандита был представлен Юэ и др. (2012)^[65] Чтобы смоделировать компромисс между исследованием и эксплуатацией для относительной обратной связи. В этом варианте игроку разрешено использовать два рычага одновременно, но он получает только двоичную обратную связь, указывающую, какой рычаг обеспечивает лучшую награду. Сложность этой проблемы связана с тем, что игрок не имеет возможности напрямую наблюдать за вознаграждением за свои действия. Самыми ранними алгоритмами решения этой проблемы являются InterleaveFiltering,^[65] Beat-The-Mean.^[66]Относительная обратная связь дуэлянтных бандитов также может привести к парадоксы голосования. Решение - взять Кондорсе победитель в качестве справки.^[67]

Совсем недавно исследователи обобщили алгоритмы от традиционных MAB до дуэлей бандитов: относительные верхние границы уверенности (RUCB),^[68] Относительное экспоненциальное взвешивание (REX3),^[69] Границы уверенности Коупленда (CCB),^[70] Относительная минимальная эмпирическая дивергенция (RMED),^[71] и двойная выборка Томпсона (DTS).^[72]

Коллаборативный бандит

Бандиты с совместной фильтрацией (то есть COFIBA) были представлены Ли, Карацоглу и Джентиле (SIGIR, 2016),^[73] где классическая совместная фильтрация и методы фильтрации на основе содержимого пытаются изучить статическую модель рекомендаций с учетом обучающих данных. Эти подходы далеки от идеала в высокодинамичных областях рекомендаций, таких как рекомендация новостей и вычислительная реклама, где набор элементов и пользователей очень изменчив.В этой работе они исследуют метод адаптивной кластеризации для рекомендаций по контенту, основанный на стратегиях исследования и эксплуатации в контекстных условиях многорукого бандита.^[74] Их алгоритм (COFIBA, произносится как «Coffee Bar») учитывает совместные эффекты^[73] которые возникают из-за взаимодействия пользователей с элементами, динамически группируя пользователей на основе рассматриваемых элементов и, в то же время, группируя элементы на основе подобия кластеризации, наведенной для пользователей. Таким образом, полученный алгоритм использует преимущества шаблонов предпочтений в данных способом, подобным методам совместной фильтрации. Они обеспечивают эмпирический анализ реальных наборов данных среднего размера, демонстрируя масштабируемость и повышенную эффективность прогнозирования (измеряемую по показателю CTR) по сравнению с современными методами кластеризации бандитов. Они также предоставляют анализ сожаления в рамках стандартной линейной настройки стохастического шума.

Комбинаторный бандит

Комбинаторная проблема многорукого бандита (CMAB)^[75][76][77] возникает, когда вместо отдельной дискретной переменной для выбора агенту нужно выбрать значения для набора переменных. Предполагая, что каждая переменная дискретна, количество возможных вариантов на итерацию экспоненциально зависит от количества переменных. Некоторые настройки CMAB были изучены в литературе, начиная с настроек, где переменные являются двоичными.^[76] к более общей настройке, где каждая переменная может принимать произвольный набор значений.^[77]

Смотрите также

• Индекс Гиттинса - мощная общая стратегия для анализа проблем бандитов.
• Жадный алгоритм
• Оптимальная остановка
• Теория поиска
• Стохастическое планирование

Рекомендации

1. Auer, P .; Cesa-Bianchi, N .; Фишер, П. (2002). "Конечный анализ проблемы многорукого бандита". Машинное обучение. 47 (2/3): 235–256. Дои:10.1023 / А: 1013689704352.
2. Katehakis, M.N .; Вейнотт, А. Ф. (1987). «Проблема многорукого бандита: разложение и вычисление». Математика исследования операций. 12 (2): 262–268. Дои:10.1287 / moor.12.2.262. S2CID  656323.
3. Гиттинс, Дж. К. (1989), Показатели распределения многоруких бандитов, Серия Wiley-Interscience по системам и оптимизации., Чичестер: John Wiley & Sons, Ltd., ISBN  978-0-471-92059-5
4. Берри, Дональд А.; Фристедт, Берт (1985), Бандитские задачи: последовательное размещение экспериментов, Монографии по статистике и прикладной теории вероятностей, Лондон: Chapman & Hall, ISBN  978-0-412-24810-8
5. Вебер, Ричард (1992), «Об индексе Гиттинса для многоруких бандитов», Анналы прикладной вероятности, 2 (4): 1024–1033, Дои:10.1214 / aoap / 1177005588, JSTOR  2959678
6. Роббинс, Х. (1952). «Некоторые аспекты последовательного планирования экспериментов». Бюллетень Американского математического общества. 58 (5): 527–535. Дои:10.1090 / S0002-9904-1952-09620-8.
7. Дж. К. Гиттинс (1979). «Бандитские процессы и индексы динамического размещения». Журнал Королевского статистического общества. Серия B (Методологическая). 41 (2): 148–177. Дои:10.1111 / j.2517-6161.1979.tb01068.x. JSTOR  2985029.
8. Press, Уильям Х. (2009), «Бандитские решения обеспечивают единые этические модели для рандомизированных клинических испытаний и сравнительных исследований эффективности», Труды Национальной академии наук, 106 (52): 22387–22392, Bibcode:2009PNAS..10622387P, Дои:10.1073 / pnas.0912378106, ЧВК  2793317, PMID  20018711.
9. Пресса (1986)
10. Брочу, Эрик; Хоффман, Мэтью В .; де Фрейтас, Нандо (сентябрь 2010 г.), Распределение портфеля для байесовской оптимизации, arXiv:1009.5419, Bibcode:2010arXiv1009.5419B
11. Шэнь, Вэйвэй; Ван, Цзюнь; Цзян, Юй-Ган; Чжа, Хунъюань (2015), «Портфолио выбора с ортогональным бандитским обучением», Труды международных совместных конференций по искусственному интеллекту (IJCAI2015)
12. Фариас, Вивек Ф; Ритеш, Мадан (2011), "Необратимая проблема многорукого бандита", Исследование операций, 59 (2): 383–399, CiteSeerX  10.1.1.380.6983, Дои:10.1287 / opre.1100.0891
13. Уиттл, Питер (1979), «Обсуждение статьи доктора Гиттинса», Журнал Королевского статистического общества, Серия B, 41 (2): 148–177, Дои:10.1111 / j.2517-6161.1979.tb01069.x
14. Верморель, Джоаннес; Мохри, Мехриар (2005), Алгоритмы многоруких бандитов и эмпирическая оценка (PDF), In European Conference on Machine Learning, Springer, pp. 437–448.
15. Уиттл, Питер (1988), «Беспокойные бандиты: распределение активности в меняющемся мире», Журнал прикладной теории вероятностей, 25А: 287–298, Дои:10.2307/3214163, JSTOR  3214163, МИСТЕР  0974588
16. Уиттл, Питер (1981), «Оружие бандиты», Анналы вероятности, 9 (2): 284–292, Дои:10.1214 / aop / 1176994469
17. Auer, P .; Cesa-Bianchi, N .; Freund, Y .; Шапир, Р. Э. (2002). «Проблема нестохастического многорукого бандита». SIAM J. Comput. 32 (1): 48–77. CiteSeerX  10.1.1.130.158. Дои:10.1137 / S0097539701398375.
18. Lai, T.L .; Роббинс, Х. (1985). «Асимптотически эффективные адаптивные правила распределения». Успехи в прикладной математике. 6 (1): 4–22. Дои:10.1016/0196-8858(85)90002-8.
19. Katehakis, M.N .; Роббинс, Х. (1995). «Последовательный выбор из нескольких популяций». Труды Национальной академии наук Соединенных Штатов Америки. 92 (19): 8584–5. Bibcode:1995PNAS ... 92.8584K. Дои:10.1073 / пнас.92.19.8584. ЧВК  41010. PMID  11607577.
20. Burnetas, A.N .; Катехакис, М. (1996). «Оптимальные адаптивные политики для задач последовательного распределения». Успехи в прикладной математике. 17 (2): 122–142. Дои:10.1006 / aama.1996.0007.
21. Burnetas, A.N .; Катехакис, М. (1997). «Оптимальные адаптивные политики для марковских процессов принятия решений». Математика. Опер. Res. 22 (1): 222–255. Дои:10.1287 / moor.22.1.222.
22. Tewari, A .; Бартлетт, П. (2008). «Оптимистическое линейное программирование порождает логарифмическое сожаление по поводу неприводимых MDP» (PDF). Достижения в системах обработки нейронной информации. 20. CiteSeerX  10.1.1.69.5482.
23. Ортнер, Р. (2010). «Онлайн-границы сожаления для марковских процессов принятия решений с детерминированными переходами». Теоретическая информатика. 411 (29): 2684–2695. Дои:10.1016 / j.tcs.2010.04.005.
24. Филиппи, С., Каппе, О., Гаривье, А. (2010). «Онлайн-границы сожаления для марковских процессов принятия решений с детерминированными переходами», Связь, управление и вычисления (Allerton), 48-я ежегодная конференция Allerton, 2010 г., стр. 115–122
25. Honda, J .; Такемура, А. (2011). «Асимптотически оптимальная политика для моделей с конечной поддержкой в ​​проблеме многорукого бандита». Машинное обучение. 85 (3): 361–391. arXiv:0905.2776. Дои:10.1007 / s10994-011-5257-4. S2CID  821462.
26. Авербек, Б. Б. (2015). «Теория выбора в бандитских задачах, выборке информации и поиске пищи». PLOS вычислительная биология. 11 (3): e1004164. Bibcode:2015PLSCB..11E4164A. Дои:10.1371 / journal.pcbi.1004164. ЧВК  4376795. PMID  25815510.
27. Costa, V.D .; Авербек, Б. Б. (2019). «Подкорковые субстраты решений исследования-эксплуатации у приматов». Нейрон. 103 (3): 533–535. Дои:10.1016 / j.neuron.2019.05.017. ЧВК  6687547. PMID  31196672.
28. Бунефуф, Д. (2019). Оптимальное использование кластеризации и исторической информации в многоруком бандите. Материалы двадцать восьмой международной совместной конференции по искусственному интеллекту. AAAI. Soc. С. 270–279. Дои:10.1109 / sfcs.2000.892116. ISBN  978-0769508504. S2CID  28713091.
29. Саттон, Р. С. и Барто, А. Г. 1998 Обучение с подкреплением: введение. Кембридж, Массачусетс: MIT Press.
30. Токич, Мишель (2010), «Адаптивное ε-жадное исследование в обучении с подкреплением на основе различий в ценностях» (PDF), KI 2010: Достижения в области искусственного интеллекта, Конспект лекций по информатике, 6359, Springer-Verlag, стр. 203–210, CiteSeerX  10.1.1.458.464, Дои:10.1007/978-3-642-16111-7_23, ISBN  978-3-642-16110-0.
31. Токич, Мишель; Пальма, Гюнтер (2011), «Исследование, основанное на разнице ценностей: адаптивное управление между Epsilon-Greedy и Softmax» (PDF), KI 2011: Достижения в области искусственного интеллекта, Конспект лекций по информатике, 7006, Springer-Verlag, стр. 335–346, ISBN  978-3-642-24455-1.
32. Гимельфарб, Мишель; Саннер, Скотт; Ли, Чи-Гун (2019), "ε-BMC: байесовский ансамблевой подход к поиску Epsilon-Greedy в безмодельном обучении с подкреплением" (PDF), Труды тридцать пятой конференции по неопределенности в искусственном интеллекте, AUAI Press, стр. 162.
33. Bouneffouf, D .; Bouzeghoub, A .; Гансарски, А. Л. (2012). «Алгоритм контекстного бандита для мобильной контекстно-зависимой рекомендательной системы». Обработка нейронной информации. Конспект лекций по информатике. 7665. п. 324. Дои:10.1007/978-3-642-34487-9_40. ISBN  978-3-642-34486-2.
34. Скотт, С. (2010), «Современный байесовский взгляд на многорукого бандита», Прикладные стохастические модели в бизнесе и промышленности, 26 (2): 639–658, Дои:10.1002 / asmb.874
35. Оливье Шапель, Лихонг Ли (2011), «Эмпирическая оценка выборки Томпсона», Достижения в системах обработки нейронной информации 24 (NIPS), Curran Associates: 2249–2257
36. Бунефуф, Д. (2018). «Включение поведенческих ограничений в онлайн-системы ИИ». Тридцать третья конференция AAAI по искусственному интеллекту (AAAI-19). AAAI: 270–279. arXiv:1809.05720. https://arxiv.org/abs/1809.05720%7Cyear=2019
37. Лэнгфорд, Джон; Чжан, Тонг (2008), «Жадный по эпохе алгоритм для контекстных многоруких бандитов», Достижения в системах обработки нейронной информации 20, Curran Associates, Inc., стр. 817–824.
38. Лихонг Ли, Вэй Чу, Джон Лэнгфорд, Роберт Э. Шапайр (2010), «Контекстно-бандитский подход к персонализированным рекомендациям новостных статей», Материалы 19-й Международной конференции по всемирной паутине (WWW 2010): 661–670, arXiv:1003.0146, Bibcode:2010arXiv1003.0146L, Дои:10.1145/1772690.1772758, ISBN  9781605587998, S2CID  207178795
39. Вэй Чу, Лихонг Ли, Лев Рейзин, Роберт Э. Шапир (2011), «Контекстные бандиты с линейными функциями выигрыша» (PDF), Материалы 14-й Международной конференции по искусственному интеллекту и статистике (AISTATS): 208–214
40. Ауэр, П. (2000). «Использование верхних доверительных границ для онлайн-обучения». Материалы 41-го ежегодного симпозиума по основам информатики. IEEE Comput. Soc. С. 270–279. Дои:10.1109 / sfcs.2000.892116. ISBN  978-0769508504. S2CID  28713091. Отсутствует или пусто | название = (помощь)
41. Хонг, Цунг-Пей; Песня, Вэй-Пин; Чиу, Чу-Тянь (ноябрь 2011 г.). Эволюционная кластеризация составных атрибутов. 2011 Международная конференция по технологиям и приложениям искусственного интеллекта. IEEE. Дои:10.1109 / taai.2011.59. ISBN  9781457721748. S2CID  14125100.
42. Оптимальное использование кластеризации и исторической информации в многоруком бандите.
43. Бунефуф, Д. (2019). Оптимальное использование кластеризации и исторической информации в многоруком бандите. Материалы двадцать восьмой международной совместной конференции по искусственному интеллекту. AAAI. Soc. С. 270–279. Дои:10.1109 / sfcs.2000.892116. ISBN  978-0769508504. S2CID  28713091.
44. Риголе, Филипп; Зееви, Ассаф (2010), Непараметрические бандиты с ковариатами, Конференция по теории обучения, COLT 2010, arXiv:1003.1630, Bibcode:2010arXiv1003.1630R
45. Сливкинс, Александр (2011), Контекстные бандиты с информацией о сходстве. (PDF), Конференция по теории обучения, COLT 2011
46. Перше, Вианни; Риголле, Филипп (2013), "Проблема многорукого бандита с ковариатами", Анналы статистики, 41 (2): 693–721, arXiv:1110.6084, Дои:10.1214 / 13-aos1101, S2CID  14258665
47. Сара Филиппи, Оливье Каппе, Орельен Гаривье, Чаба Сепешвари (2010), "Параметрические бандиты: обобщенный линейный случай", Достижения в системах обработки нейронной информации 23 (NIPS), Curran Associates: 586–594
48. Лихонг Ли, Ю Лу, Дэнъюн Чжоу (2017), «Доказательно оптимальные алгоритмы для обобщенных линейных контекстных бандитов», Материалы 34-й Международной конференции по машинному обучению (ICML): 2071–2080, arXiv:1703.00048, Bibcode:2017arXiv170300048L
49. Кванг-Сунг Джун, Анируддха Бхаргава, Роберт Д. Новак, Ребекка Уиллетт (2017), «Масштабируемые обобщенные линейные бандиты: онлайн-вычисления и хеширование», Достижения в системах обработки нейронной информации 30 (NIPS), Curran Associates: 99–109, arXiv:1706.00136, Bibcode:2017arXiv170600136J
50. Бранислав Кветон, Манзил Захир, Чаба Сепешвари, Лихонг Ли, Мохаммад Гавамзаде, Крейг Бутилье (2020), «Рандомизированное исследование обобщенных линейных бандитов», Материалы 23-й Международной конференции по искусственному интеллекту и статистике (AISTATS), arXiv:1906.08947, Bibcode:2019arXiv190608947K
51. Аллезиардо, Робин; Феро, Рафаэль; Джаллель, Бунефуф (2014), «Комитет по нейронным сетям для решения проблемы контекстного бандита», Обработка нейронной информации - 21-я международная конференция, ICONIP 2014, Малайзия, 03-06 ноября 2014 г., Труды, Конспект лекций по информатике, 8834, Springer, стр. 374–381, arXiv:1409.8191, Дои:10.1007/978-3-319-12637-1_47, ISBN  978-3-319-12636-4, S2CID  14155718
52. Михал Валко; Натан Корда; Реми Муньос; Илиас Флаунас; Нелло Кристианини (2013), Конечный временной анализ кернелизованных контекстных бандитов, 29-я конференция по неопределенности в искусственном интеллекте (UAI 2013) и (JFPDA 2013)., arXiv:1309.6869, Bibcode:2013arXiv1309.6869V
53. Феро, Рафаэль; Аллезиардо, Робин; Урвой, Танги; Клеро, Фабрис (2016). «Случайный лес для контекстной проблемы бандитов». Аистатс: 93–101.
54. Алех Агарвал, Дэниел Дж. Хсу, Сатьен Кале, Джон Лэнгфорд, Лихонг Ли, Роберт Э. Шапир (2014), «Укрощение монстра: быстрый и простой алгоритм для контекстных бандитов», Материалы 31-й Международной конференции по машинному обучению (ICML): 1638–1646, arXiv:1402.0555, Bibcode:2014arXiv1402.0555A
55. Контекстный бандит с ограниченным контекстом, Джаллель Бунефуф, 2017 <https://www.ijcai.org/Proceedings/2017/0203.pdf >
56. Баданидиюру, А .; Langford, J .; Сливкинс, А. (2014), «Находчивые контекстные бандиты» (PDF), Материалы конференции по теории обучения (COLT)
57. Ву, Хуасень; Срикант, Р .; Лю, Синь; Цзян, Чонг (2015), «Алгоритмы с логарифмическим или сублинейным сожалением для ограниченных контекстных бандитов», 29-я ежегодная конференция по системам обработки нейронной информации (NIPS), Curran Associates: 433–441, arXiv:1504.06937, Bibcode:2015arXiv150406937W
58. Буртини, Джузеппе, Джейсон Лёппки и Рамон Лоуренс. «Обзор онлайн-экспериментов со стохастическим многоруким бандитом». препринт arXiv arXiv:1510.00757 (2015).
59. Селдин, Ю., Сепесвари, К., Ауэр, П. и Аббаси-Ядкори, Ю., 2012 г., декабрь. Оценка и анализ производительности алгоритма EXP3 в стохастических средах. В EWRL (стр. 103–116).
60. Хаттер, М. и Польша, Дж., 2005. Адаптивное онлайн-прогнозирование по следам взволнованного лидера. Journal of Machine Learning Research, 6 (апрель), стр.639–660.
61. UCB со скидкой, Левенте Кочиш, Чаба Сепешвари, 2006
62. О политике верхнего уровня доверия для проблем нестационарных бандитов, Гаривье и Мулин, 2008 г. <https://arxiv.org/abs/0805.3415 >
63. Улучшение маркетинговых экспериментов в Интернете с помощью дрейфующих многоруких бандитов, Джузеппе Буртини, Джейсон Лоэппки, Рамон Лоуренс, 2015 <http://www.scitepress.org/DigitalLibrary/PublicationsDetail.aspx?ID=Dx2xXEB0PJE=&t=1 >
64. Бунефуф, Джаллель; Феро, Рафаэль (2016), «Проблема многорукого бандита с известной тенденцией», Нейрокомпьютинг
65. Юэ, Исун; Бродер, Йозеф; Клейнберг, Роберт; Иоахим, Торстен (2012), «Проблема дуэльных бандитов с K-вооруженными стрелами», Журнал компьютерных и системных наук, 78 (5): 1538–1556, CiteSeerX  10.1.1.162.2764, Дои:10.1016 / j.jcss.2011.12.028
66. Юэ, Исун; Иоахимс, Торстен (2011), «Победите злого бандита», Материалы ICML'11
67. Урвой, Танги; Клеро, Фабрис; Феро, Рафаэль; Наамане, Сами (2013), «Обычная разведка и голосующие бандиты с K» (PDF), Материалы 30-й Международной конференции по машинному обучению (ICML-13)
68. Зоги, Масрур; Уайтсон, Шимон; Муньос, Реми; Рийке, Маартен Д. (2014), «Относительно верхний предел уверенности для проблемы вооруженных дуэльных бандитов на сумму $ K $» (PDF), Материалы 31-й Международной конференции по машинному обучению (ICML-14)
69. Гаджане, Пратик; Урвой, Танги; Клеро, Фабрис (2015), «Алгоритм относительного экспоненциального взвешивания для состязательных бандитов, основанных на полезности» (PDF), Материалы 32-й Международной конференции по машинному обучению (ICML-15)
70. Зоги, Масрур; Карнин, Зохар С; Уайтсон, Шимон; Рийке, Маартен Д. (2015), «Дуэльные бандиты Коупленда», Достижения в системах обработки нейронной информации, NIPS'15, arXiv:1506.00312, Bibcode:2015arXiv150600312Z
71. Комияма, Дзюнпей; Хонда, Джунья; Кашима, Хисаси; Накагава, Хироши (2015), "Сожалею о нижней границе и оптимальном алгоритме в задаче" Дуэльный бандит " (PDF), Материалы 28-й конференции по теории обучения
72. Ву, Хуасень; Лю, Синь (2016), «Двойная выборка Томпсона для дуэлянтных бандитов», 30-я ежегодная конференция по системам обработки нейронной информации (NIPS), arXiv:1604.07101, Bibcode:2016arXiv160407101W
73. Ли, Шуай; Александрос, Карацоглу; Джентиле, Клаудио (2016), «Бандиты совместной фильтрации», 39-я Международная конференция ACM SIGIR по поиску информации (SIGIR 2016), arXiv:1502.03473, Bibcode:2015arXiv150203473L
74. Джентиле, Клаудио; Ли, Шуай; Запелла, Джованни (2014), «Онлайн-кластеризация бандитов», 31-я Международная конференция по машинному обучению, Журнал исследований в области машинного обучения (ICML 2014), arXiv:1401.8257, Bibcode:2014arXiv1401.8257G
75. Гай Ю., Кришнамачари Б. и Джайн Р. (2010), Изучение распределения многопользовательских каналов в когнитивных радиосетях: комбинаторная формулировка многорукого бандита (PDF), стр. 1–9
76. Чен, Вэй и Ван, Яцзюнь и Юань, Ян (2013), Комбинаторный многорукий бандит: общие основы и приложения (PDF), стр. 151–159
77. Сантьяго Онтаньон (2017), «Комбинаторные многорукие бандиты для стратегических игр в реальном времени», Журнал исследований искусственного интеллекта, 58: 665–702, arXiv:1710.04805, Bibcode:2017arXiv171004805O, Дои:10.1613 / jair.5398, S2CID  8517525

дальнейшее чтение

• Guha, S .; Munagala, K .; Ши, П. (2010). «Алгоритмы аппроксимации проблем неугомонных бандитов». Журнал ACM. 58: 1–50. arXiv:0711.3861. Дои:10.1145/1870103.1870106. S2CID  1654066.
• Даяник, С .; Powell, W .; Ямадзаки, К. (2008), «Политика индексации для проблем дисконтированных бандитов с ограничениями доступности», Достижения в прикладной теории вероятностей, 40 (2): 377–400, Дои:10.1239 / aap / 1214950209.
• Пауэлл, Уоррен Б. (2007), «Глава 10», Приближенное динамическое программирование: избавление от проклятия размерности, Нью-Йорк: Джон Уайли и сыновья, ISBN  978-0-470-17155-4.
• Роббинс, Х. (1952), «Некоторые аспекты последовательного планирования экспериментов», Бюллетень Американского математического общества, 58 (5): 527–535, Дои:10.1090 / S0002-9904-1952-09620-8.
• Саттон, Ричард; Барто, Эндрю (1998), Обучение с подкреплением, MIT Press, ISBN  978-0-262-19398-6, заархивировано из оригинал на 2013-12-11.

• Аллезиардо, Робин (2014), «Комитет по нейронным сетям для решения проблемы контекстного бандита», Обработка нейронной информации - 21-я международная конференция, ICONIP 2014, Малайзия, 03-06 ноября 2014 г., Труды, Конспект лекций по информатике, 8834, Springer, стр. 374–381, arXiv:1409.8191, Дои:10.1007/978-3-319-12637-1_47, ISBN  978-3-319-12636-4, S2CID  14155718.

• Вебер, Ричард (1992), «Об индексе Гиттинса для многоруких бандитов», Анналы прикладной вероятности, 2 (4): 1024–1033, Дои:10.1214 / aoap / 1177005588, JSTOR  2959678.
• Катехакис, М. и С. Дерман (1986), «Вычисление оптимальных правил последовательного распределения в клинических испытаниях», Адаптивные статистические процедуры и связанные темы, Конспект лекций Института математической статистики - серия монографий, 8, стр. 29–39, Дои:10.1214 / нм / 1215540286, ISBN  978-0-940600-09-6, JSTOR  4355518.
• Катехакис, М. и А. Ф. Вейнотт младший (1987), «Проблема многорукого бандита: разложение и вычисление», Математика исследования операций, 12 (2): 262–268, Дои:10.1287 / moor.12.2.262, JSTOR  3689689, S2CID  656323.

внешняя ссылка

• MABWiser, Открытый исходный код Реализация бандитских стратегий на Python, которая поддерживает контекстные, параметрические и непараметрические контекстные политики со встроенными возможностями распараллеливания и моделирования.
• PyMaBandits, Открытый исходный код реализация бандитских стратегий в Python и Matlab.
• Контекстуальный, Открытый исходный код р пакет, упрощающий моделирование и оценку как контекстно-свободных, так и контекстных политик Multi-Armed Bandit.
• bandit.sourceforge.net Бандитский проект, реализация бандитских стратегий с открытым исходным кодом.
• Banditlib, Открытый исходный код реализация бандитских стратегий на C ++.
• Лесли Пак Кельблинг и Майкл Л. Литтман (1996). Эксплуатация против разведки: случай единственного государства.
• Учебник: Введение в бандитов: алгоритмы и теория. Часть 1. Часть 2.
• Ресторанная проблема Фейнмана, классический пример (с известным ответом) компромисса между эксплуатацией и разведкой.
• Алгоритмы Bandit против тестирования AB.
• С. Бубек и Н. Чеза-Бьянки Обзор бандитов.
• Обзор контекстных многоруких бандитов, обзор / руководство для Contextual Bandits.
• Сообщение в блоге о стратегиях многоруких бандитов с кодом Python.
• Анимированные интерактивные сюжеты иллюстрируя жадность Эпсилона, Выборка Томпсона и стратегии балансировки разведки / эксплуатации на уровне верхней границы уверенности.