Кубики Miwins - Miwins dice

Игральные кости Мивина

Кубики Мивина сделаны из титан
Дизайнер (ы)	Д-р Михаэль Винкельманн
Издатель (ы)	Arquus Verlag Вена
Активные годы	1994
Игроки	1–9
Время игры	5–60 минут, в зависимости от игры
Возрастной диапазон	6+, в зависимости от игры
Интернет сайт	www.miwin.com

Игральные кости Мивина представляют собой набор нетранзитивные кости изобретен в 1975 году физиком Михаэлем Винкельманном. Они состоят из трех разных игральная кость с лица номера подшипников от 1 до 9; сумма противоположных граней равна 9, 10 или 11. Числа на каждом кубике дают сумму 30 и имеют среднее арифметическое из 5.

Описание

Кубики Мивина IX, X, XI

У кубиков Мивина 6 сторон, на каждой из которых есть число, изображенное в виде точек. Стандартный набор выполнен из дерева; специальные конструкции изготавливаются из титана или других материалов (золото, серебро).

Первый набор кубиков Мивина: III, IV, V

дизайн чисел кубиков Miwins III, IV, V

Каждый кубик назван по сумме двух наименьших чисел. Точки на каждом кубике окрашены в синий, красный или черный цвет. На каждом кубике есть следующие номера:

Die III	с красный точки	1	2			5	6	7		9
Умереть IV	с синий точки	1		3	4	5			8	9
Die V	с чернить точки		2	3	4		6	7	8

Числа 1 и 9, 2 и 7, 3 и 8 находятся на противоположных сторонах всех трех кубиков. Дополнительные числа: 5 и 6 на кубике III, 4 и 5 на кубике IV и 4 и 6 на кубике V. Кубики разработаны таким образом, что на каждом кубике обычно побеждает другой. В вероятность что на данном кубике в последовательности (III, IV, V, III) будет выброшено большее число, чем следующее в последовательности 17/36; меньшее число, 16/36. Таким образом, III имеет тенденцию выигрывать у IV, IV против V и V против III. Такие кости известны как нетранзитивный.

Второй набор кубиков Мивина: IX, X, XI

дизайн номеров кубиков Miwins IX, X, XI

Каждый кубик назван по сумме его самого низкого и самого высокого чисел. Точки на каждом кубике окрашены в желтый, белый или зеленый цвет. На каждом кубике есть следующие номера:

Die IX	с желтый точки	1		3		5	6	7	8
Die X	с белый точки	1	2		4		6		8	9
Die XI	с зеленый точки		2	3	4	5		7		9

В вероятность что на данном кубике в последовательности (XI, X, IX, XI) будет выброшено большее число, чем следующее в последовательности 17/36; меньшее число, 16/36. Таким образом, XI имеет тенденцию выигрывать против X, X против IX и IX против XI.

Третий и четвертый набор кубиков Мивина

Третий набор:

Die MW 5	с синий числа					5	6	7	8							15	16
Die MW 3	с красный числа			3	4							11	12	13	14
Die MW 1	с чернить числа	1	2							9	10							17	18

четвертый набор:

Die MW 6	с желтый числа					5	6			9	10			13	14
Die MW 4	с белый числа			3	4			7	8									17	18
Die MW 2	с зеленый числа	1	2									11	12			15	16

В вероятность что данный кубик в первой последовательности (5, 3, 1, 5) или второй последовательности (6, 4, 2, 6) выпадет большее число, чем следующее в последовательности 5/9; меньшее число, 4/9.

Математические атрибуты

У кубиков в первом и втором наборах Miwin схожие атрибуты: на каждой кубике каждое из своих чисел нанесено ровно один раз, сумма чисел равна 30, и каждое число от 1 до 9 дважды распределяется по трем кубикам. Этот атрибут характеризует реализацию непереходных игральных костей, позволяя использовать различные варианты игры. Во всех играх требуется всего 3 кубика по сравнению с другими теоретическими нетранзитивными кубиками, разработанными с учетом математики, такими как Кости Эфрона.^[1]

Вероятности

• 1/3 номинальной стоимости штампа можно разделить на 3 без переноса.
• 1/3 номинальных значений штампа можно разделить на 3 с переносом 1.
• 1/3 номинальной стоимости штампа можно разделить на 3 с переносом 2.

Вероятность для данного числа со всеми 3 кубиками составляет 11/36, для данного выпавшего двойного числа - 1/36, для любого выпавшего двойного числа - 1/4. Вероятность получить выпавший дубль составляет всего 50% по сравнению с обычными кубиками.

Накопленная частота

• 

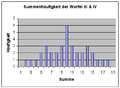
  Кумулятивная частота III и IV типов

• 

  Кумулятивная частота III и V типов

• 

  Кумулятивная частота IV и V типов

• 

  Совокупная частота типов III и IV и V = "Распределение Мивина"

Обратная непереносимость

Удаление общих точек на костях Мивина отменяет непереходность.^{[нужна цитата ]}

Die III	с синий точки	1	2			5	6	7		9	→ Die III '	2	6	7
Умереть IV	с красный точки	1		3	4	5			8	9	→ Die IV '	3	4	8

III: IV = 17:16, III ': IV' = 4: 5 → IV '> III' аналог: III / V, IV / V

Равное распределение случайных чисел

Игральные кости Мивина позволяют генерировать числа на случайный в пределах заданного диапазона, так что каждое включенное число встречается с равной вероятностью. Чтобы получить диапазон, который не начинается с 1 или 0, просто добавьте постоянное значение, чтобы привести его в этот диапазон (чтобы получить случайные числа от 8 до 16 включительно, следуйте 1 – 9 инструкции ниже и прибавьте 7 к результату каждого броска).

• 1 – 9: Бросается 1 кубик (выбирается случайным образом): P (1) = P (2) = ... = P (9) = 1/9
• 0 – 80: Бросается 2 кубика (выбираются наугад), всегда вычитается 1: P (0) = P (1) = ... = P (80) = 1 / 9² = 1/81

Другие дистрибутивы

0 - 90 (бросить 3 раза)

Управляющая вероятность: P (0) = P (1) = ... = P (90) = 8 / 9³ = 8/729

Чтобы получить равное распределение с числами от 0 до 90, все три кубика бросаются по одному в случайном порядке. Результат рассчитывается по следующим правилам:

• 1-й бросок равен 9, 3-й бросок не 9: дает 10 раз 2-й бросок (возможные баллы: 10, 20, 30, 40, 50, 60, 70, 80, 90)
• 1-й бросок не равен 9: дает 10 раз 1-й бросок плюс 2-й бросок
• 1-й бросок равен 3-му: дает 2-й бросок (возможные оценки: 1, 2, 3, 4, 5, 6, 7, 8, 9)
• Все кубики равны: дает 0
• Все кости 9: нет очков

Образец:

1-й бросок	2-й бросок	3-й бросок	Уравнение	Результат
9	9	не 9	10 раз 9	90
9	1	не 9	10 раз 1	10
8	4	не 8	(10 раз по 8) + 4	84
1	3	не 1	(10 раз по 1) + 3	13
7	8	7	7 = 7, дает 8	8
4	4	4	все равны	0
9	9	9	все 9	-

Это дает 91 число от 0 до 90 с вероятностью 8 / 9³, 8 × 91 = 728 = 9³ - 1.

0-103 (бросить 3 раза)

Управляющая вероятность: P (0) = P (1) = ... = P (103) = 7 / 9³ = 7/729

Это дает 104 числа от 0 до 103 с вероятностью 7 / 9³, 7 × 104 = 728 = 9³ - 1.

0 - 728 (бросить 3 раза)

Управляющая вероятность: P (0) = P (1) = ... = P (728) = 1 / 9³ = 1/729

Это дает 729 чисел от 0 до 728 с вероятностью 1 / 9³.

За раз бросается один кубик, взятый наугад.

Создать система счисления базы 9:

• Из номинальной стоимости каждого броска необходимо вычесть 1, потому что в этой системе счисления всего 9 цифр (0,1,2,3,4,5,6,7,8)
• (1-й бросок) × 81 + (2-й бросок) × 9 + (3-й бросок) × 1

Эта система дает следующий максимум: 8 × 9² + 8 × 9 + 8 × 9 ° = 648 + 72 + 8 = 728 = 9³ - 1

Примеры:

1-й бросок	2-й бросок	3-й бросок	Уравнение	Результат
9	9	9	8 × 9² + 8 × 9 + 8	728
4	7	2	3 × 9² + 6 × 9 + 1	298
2	4	1	1 × 9² + 4 × 9 + 0	117
1	3	4	0 × 9² + 3 × 9 + 3	30
7	7	7	6 × 9² + 6 × 9 + 6	546
1	1	1	0 × 9² + 0 × 9 + 0	0
4	2	6	3 × 9² + 1 × 9 + 5	257

Комбинации с кубиками Мивина III, IV и V типов

Вариант	Уравнение	количество вариантов
один бросок с 3 кубиками, тип не используется как атрибут	-	135
один бросок с 3 кубиками, тип - дополнительный атрибут	(135 – 6 × 9) × 2 + 54	216
1 бросок с каждым типом, тип не используется как атрибут	6 × 6 × 6	216
1 бросок с каждым типом, тип используется как атрибут	6 × 6 × 6 × 6	1296
3 броска, случайный выбор одного из кубиков для каждого броска, тип не используется как атрибут	9 × 9 × 9	729

3 броска, случайный выбор одного из кубиков для каждого броска, в качестве атрибута используется тип:

Вариант	Уравнение	количество альтернатив
III, III, III / IV, IV, IV / V, V, V	3 × 6 × 6 × 6	648
III, III, IV / III, III, V / III, IV, IV / III, V, V / IV, IV, V / IV, V, V	6 × 3 × 216	+ 3888
III, IV, V / III, V, IV / IV, III, V / IV, V, III / V, III, IV / V, IV, III	6 × 216	+ 1296
		= 5832

5832 = 2 × 2 × 2 × 9 × 9 × 9 = 18³ возможных чисел.

Игры

С середины 1980-х годов об играх писала пресса.^[2] Винкельманн сам представлял игры, например, в 1987 году в Вене, на Österrechischen Spielefest, Stiftung Spielen in Österreich, Леопольдсдорф, где «Кости Мивина» выиграли приз «Новая независимая игра в кости года».

В 1989 году игры были рецензированы журналом "Die Spielwiese".^[3] В то время для игры в кости Miwin существовало 14 вариантов азартных и стратегических игр. В журнале Spielbox было два варианта игры на кости Мивина в категории "Unser Spiel im Heft" (теперь известная как "Edition Spielbox"): пасьянс 5 к 4, и стратегическая игра для двух игроков Укус.

В 1994 году венское издательство Arquus выпустило книгу Винкельмана. Göttliche Spiele,^[4] который содержал 92 игры, мастер-копию для 4 игровых досок, документацию о математических характеристиках игральных костей и набор кубиков Мивина. На сайте Винкельмана есть еще больше вариантов игр.^[5]

Были разработаны пасьянсы и игры для девяти игроков. Игры подходят для игроков старше 6 лет. Для некоторых игр требуется игровая доска; время игры варьируется от 5 до 60 минут.

Варианты 0 - 80

1 вариант

Бросаются два кубика, выбираемые случайным образом, по одному. Каждая пара подсчитывается путем умножения первой на 9 и вычитания второй из результата: 1-й бросок × 9 - 2-й бросок.

Примеры:

1-й бросок	2-й бросок	Уравнение	Результат
9	9	9 × 9 − 9	72
9	1	9 × 9 − 1	80
1	9	9 × 1 − 9	0
2	9	9 × 2 − 9	9
2	8	9 × 2 − 8	10
8	4	9 × 8 − 4	68
1	3	9 × 1 − 3	6

Этот вариант предоставляет числа от 0 до 80 с вероятностью 1 / 9² = 1/81.

2 вариант

Бросаются два кубика, выбираемые случайным образом, по одному. Пары рассчитываются по следующим правилам:

• 1-й бросок - 9: дает 10 × 2-й бросок - 10
• 1-й бросок не равен 9: дает 10 × 1-й бросок + 2-й бросок - 10

Примеры

1-й бросок	2-й бросок	Уравнение	Результат
9	9	10 × 9 − 10	80
9	1	10 × 1 − 10	0
8	4	10 × 8 + 4 − 10	74
1	3	10 × 1 + 3 − 10	3

Этот вариант предоставляет числа от 0 до 80 с вероятностью 1 / 9² = 1/81.

3 вариант

Бросаются два кубика, выбираемые случайным образом, по одному. Оценка начисляется по следующим правилам:

• Оба броска равны 9: дает 0
• 1-й бросок равен 9, а 2-й бросок не 9: дает 10 × 2-й бросок
• 1-й бросок равен 8: дает 2-й бросок
• Все остальные: дает 10 × 1-й бросок - 2-й бросок

Примеры:

1-й бросок	2-й бросок	Уравнение	Результат
9	9	-	0
9	3	10 × 3	30
8	4	1 × 4	4
5	9	5 × 10 + 9	59

Примечания

1. http://www.miwin.com/ нажмите "Miwin'sche Würfel 2", затем проверьте атрибуты
2. Австрийская газета "Das Weihnachtsorakel, Spieltip" Ein Buch mit zwei Seiten ", Стандарт 18.Dez..1994, стр. 6, Pöppel-Revue 1/1990, стр. 6 и Spielwiese 11/1990, стр. 13, 29/1994, стр. 7
3. 29/1989, стр. 6
4. Книга о немецкой версии Amazon
5. Домашняя страница Винкельмана

внешняя ссылка

• Домашняя страница продюсера Михаэля Винкельмана
• Укус в Ludings База данных игры
• Игровые тесты

Опубликованные игры

• Фридхельм Мерц: Spiel ’89. Книга для игроков, создателей игр, производителей игр и прессы. Merz Verl., Бонн 1989, ISBN  3-926108-23-1, С. 477.
• Михаэль Винкельманн: Göttliche Spiele Arquus-Verl. Паллич 1994Göttliche Spiele Arquus-Verl. Пахлич 1994, ISBN  3-901388-10-9,