Алгоритм слияния - Merge algorithm

Алгоритмы слияния семья алгоритмы это займет несколько отсортированный списки в качестве входных данных и создают единый список в качестве выходных данных, содержащий все элементы входных списков в отсортированном порядке. Эти алгоритмы используются как подпрограммы в различных алгоритмы сортировки, самый известный Сортировка слиянием.

Заявление

Пример сортировки слиянием

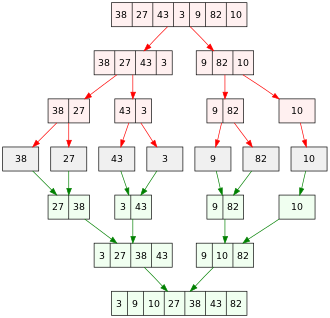
Алгоритм слияния играет важную роль в Сортировка слиянием алгоритм, а алгоритм сортировки на основе сравнения. Концептуально алгоритм сортировки слиянием состоит из двух шагов:

1. Рекурсивно разделите список на подсписки (примерно) равной длины, пока каждый подсписок не будет содержать только один элемент, или в случае итеративной (снизу вверх) сортировки слиянием рассмотрите список п элементы как п подсписки размера 1. Список, содержащий единственный элемент, по определению сортируется.
2. Неоднократно объединяйте подсписки, чтобы создать новый отсортированный подсписок, пока один список не будет содержать все элементы. Единый список - это отсортированный список.

Алгоритм слияния многократно используется в алгоритме сортировки слиянием.

Пример сортировки слиянием приведен на иллюстрации. Он начинается с несортированного массива из 7 целых чисел. Массив разделен на 7 разделов; каждый раздел содержит 1 элемент и сортируется. Затем отсортированные разделы объединяются для создания более крупных отсортированных разделов, пока не останется 1 раздел, отсортированный массив.

Объединение двух списков

Объединение двух отсортированных списков в один можно выполнить в линейное время и линейное или постоянное пространство (в зависимости от модели доступа к данным). Следующее псевдокод демонстрирует алгоритм, который объединяет входные списки (либо связанные списки или же массивы ) А и B в новый список C.^[1][2]:104 Функция голова выдает первый элемент списка; «удаление» элемента означает удаление его из списка, обычно путем увеличения указателя или индекса.

алгоритм объединить (A, B) является    входы A, B: список возвращается список C: = новый пустой список пока A не пусто, а B не пусто делать        если напор (A) ≤ напор (B) тогда            добавить голову (A) к C, отбросить голову A еще            добавьте голову (B) к C, опустите голову B // К настоящему времени либо A, либо B пусто. Осталось очистить другой список ввода.    пока А не пусто делать        добавить голову (A) к C, отбросить голову A пока B не пусто делать        добавьте голову (B) к C, опустите голову B возвращаться C

Когда входы представляют собой связанные списки, этот алгоритм может быть реализован для использования только постоянного объема рабочего пространства; указатели в узлах списков могут быть повторно использованы для бухгалтерского учета и для построения окончательного объединенного списка.

В алгоритме сортировки слиянием это подпрограмма обычно используется для объединения двух подмассивов A [lo..mid], A [mid..hi] одного массива А. Это можно сделать, скопировав подмассивы во временный массив, а затем применив описанный выше алгоритм слияния.^[1] Выделения временного массива можно избежать, но за счет скорости и простоты программирования. Были разработаны различные алгоритмы слияния на месте,^[3] иногда жертвуя линейным временем, чтобы произвести О(п бревно п) алгоритм;^[4] видеть Сортировка слиянием § Варианты для обсуждения.

K-образное слияние

Основная статья: K-способ слияния

k-way слияние обобщает двоичное слияние до произвольного числа k отсортированных списков ввода. Применение k-сходы слияния возникают в различных алгоритмах сортировки, в том числе сортировка терпения^[5] и внешняя сортировка алгоритм, который делит свой ввод на k = 1/M − 1 блоки, которые помещаются в памяти, сортирует их по одному, а затем объединяет эти блоки.^{[2]:119–120}

Существует несколько решений этой проблемы. Наивное решение - сделать цикл по k списки, чтобы каждый раз выбирать минимальный элемент, и повторять этот цикл, пока все списки не станут пустыми:

• Ввод: список k списки.
• Пока какой-либо из списков не пуст:
  • Прокрутите списки, чтобы найти тот, у которого минимальный первый элемент.
  • Выведите минимальный элемент и удалите его из списка.

В худшем случае, этот алгоритм выполняет (k−1)(п−k/2) сравнения элементов для выполнения своей работы, если в общей сложности п элементы в списках.^[6]Его можно улучшить, сохранив списки в приоритетная очередь (мин-куча ) с ключом их первого элемента:

• Постройте минимальную кучу час из k списки, используя первый элемент в качестве ключа.
• Пока какой-либо из списков не пуст:
  • Позволять я = найти-мин (час).
  • Вывести первый элемент списка я и удалите его из своего списка.
  • Re-heapify час.

Теперь поиск следующего наименьшего элемента для вывода (find-min) и восстановление порядка кучи можно выполнить в О(бревно k) время (точнее, 2⌊log k⌋ сравнения^[6]), а полную проблему можно решить в О(п бревно k) время (примерно 2п⌊бревно k⌋ сравнения).^{[6][2]:119–120}

Третий алгоритм решения проблемы - это разделяй и властвуй решение, основанное на алгоритме двоичного слияния:

• Если k = 1, вывести единый входной список.
• Если k = 2выполните двоичное слияние.
• В противном случае рекурсивно объедините первый ⌊k/2⌋ списки и окончательные ⌈k/2⌉ списки, затем двоично объединить их.

Когда входные списки для этого алгоритма упорядочены по длине, сначала самые короткие, для этого требуется меньше, чем п⌈бревно k⌉ сравнения, то есть меньше половины числа, используемого алгоритмом на основе кучи; на практике он может быть таким же быстрым или медленным, как алгоритм на основе кучи.^[6]

Параллельное слияние

А параллельно версия алгоритма двоичного слияния может служить строительным блоком параллельная сортировка слиянием. Следующий псевдокод демонстрирует этот алгоритм в параллельный принцип разделяй и властвуй стиль (адаптировано из Cormen и другие.^[7]:800). Он работает с двумя отсортированными массивами А и B и записывает отсортированный вывод в массив C. Обозначение A [я ... j] обозначает часть А из индекса я через j, эксклюзив.

алгоритм объединить (A [i ... j], B [k ... ℓ], C [p ... q]) является    входы A, B, C: массив i, j, k, ℓ, p, q: индексы позволять т = j - я, п = ℓ - к если т <п тогда        поменять местами A и B // убедитесь, что A - это больший массив: i, j все еще принадлежат A; k, ℓ к B        поменять местами m и n если м ≤ 0 тогда        возвращаться  // базовый случай, объединять нечего    позволять г = ⌊ (я + j) / 2⌋ позволять s = двоичный поиск (A [r], B [k ... ℓ]) позволять t = p + (r - i) + (s - k) C [t] = A [r] параллельно делаем        объединить (A [i ... r], B [k ... s], C [p ... t]) объединить (A [r + 1 ... j], B [s ... ℓ] , C [t + 1 ... q])

Алгоритм работает путем разделения либо А или же B, в зависимости от того, что больше, на (почти) равные половины. Затем он разбивает другой массив на часть со значениями, меньшими, чем средняя точка первого, и часть с большими или равными значениями. (The бинарный поиск подпрограмма возвращает индекс в B куда А[р] было бы, если бы это было в B; что это всегда число между k и ℓ.) Наконец, каждая пара половинок объединяется рекурсивно, а поскольку рекурсивные вызовы независимы друг от друга, они могут выполняться параллельно. Гибридный подход, при котором последовательный алгоритм используется для базового случая рекурсии, показал хорошие результаты на практике. ^[8]

В работай выполняется алгоритмом для двух массивов, содержащих в сумме п элементов, т. е. время работы его серийной версии, составляет О(п). Это оптимально, поскольку п элементы необходимо скопировать в C. Для расчета охватывать алгоритма необходимо получить Отношение рецидива. Поскольку два рекурсивных вызова слияние выполняются параллельно, необходимо учитывать только более дорогостоящий из двух вызовов. В худшем случае максимальное количество элементов в одном из рекурсивных вызовов не превышает ${ extstyle {frac {3}{4}}n}$ поскольку массив с большим количеством элементов идеально делится пополам. Добавление ${displaystyle Theta left(log(n)ight)}$ стоимость двоичного поиска, мы получаем это повторение как верхнюю границу:

${displaystyle T_{infty }^{ ext{merge}}(n)=T_{infty }^{ ext{merge}}left({frac {3}{4}}night)+Theta left(log(n)ight)}$

Решение ${displaystyle T_{infty }^{ ext{merge}}(n)=Theta left(log(n)^{2}ight)}$, что означает, что на идеальной машине с неограниченным количеством процессоров требуется столько времени.^{[7]:801–802}

Примечание: Распорядок не стабильный: если одинаковые элементы разделены разделением А и B, они будут чередоваться в C; также обмен А и B уничтожит порядок, если одинаковые элементы распределены по обоим входным массивам. В результате при использовании этого алгоритма для сортировки получается нестабильная сортировка.

Языковая поддержка

Немного компьютерные языки обеспечить встроенную или библиотечную поддержку для объединения отсортированных коллекции.

C ++

В C ++ с Стандартная библиотека шаблонов имеет функцию std :: merge, который объединяет два отсортированных диапазона итераторы, и std :: inplace_merge, который объединяет два последовательных отсортированных диапазона на месте. В дополнение std :: list (связанный список) класс имеет свой собственный слияние метод, который объединяет другой список в себя. Тип объединяемых элементов должен поддерживать меньше (<), либо он должен быть снабжен настраиваемым компаратором.

C ++ 17 допускает различные политики выполнения, а именно последовательное, параллельное и неупорядоченное параллельное выполнение.^[9]

Python

Python стандартная библиотека (начиная с версии 2.6) также имеет слияние функция в heapq модуль, который принимает несколько отсортированных итераций и объединяет их в один итератор.^[10]

Смотрите также

• Слияние (контроль версий)
• Присоединиться (реляционная алгебра)
• Присоединиться (SQL)
• Присоединиться (Unix)

Рекомендации

1. Скиена, Стивен (2010). Руководство по разработке алгоритмов (2-е изд.). Springer Science + Business Media. п. 123. ISBN  978-1-849-96720-4.
2. Курт Мельхорн; Питер Сандерс (2008). Алгоритмы и структуры данных: базовый набор инструментов. Springer. ISBN  978-3-540-77978-0.
3. Катаянен, Юрки; Пасанен, Томи; Теухола, Юкка (1996). «Практическая сортировка слиянием на месте». Nordic J. Computing. 3 (1): 27–40. CiteSeerX  10.1.1.22.8523.
4. Ким, Пок-Сон; Куцнер, Арне (2004). Стабильное слияние минимального объема памяти посредством симметричных сравнений. Европейский Symp. Алгоритмы. Конспект лекций по информатике. 3221. С. 714–723. CiteSeerX  10.1.1.102.4612. Дои:10.1007/978-3-540-30140-0_63. ISBN  978-3-540-23025-0.
5. Чандрамули, Бадриш; Гольдштейн, Джонатан (2014). Терпение - это добродетель: пересмотр слияния и сортировки на современных процессорах. SIGMOD / PODS.
6. Грин, Уильям А. (1993). k-way слияние и k-арная сортировка (PDF). Proc. 31-я ежегодная Юго-восточная конференция ACM. С. 127–135.
7. Кормен, Томас Х.; Лейзерсон, Чарльз Э.; Ривест, Рональд Л.; Штейн, Клиффорд (2009) [1990]. Введение в алгоритмы (3-е изд.). MIT Press и McGraw-Hill. ISBN  0-262-03384-4.
8. Виктор Юрьевич Дуваненко (2011), «Параллельное слияние», Журнал доктора Добба
9. "std: merge". cppreference.com. 2018-01-08. Получено 2018-04-28.
10. https://docs.python.org/library/heapq.html#heapq.merge

дальнейшее чтение

• Дональд Кнут. Искусство программирования, Том 3: Сортировка и поиск, Третье издание. Аддисон-Уэсли, 1997. ISBN  0-201-89685-0. Страницы 158–160 раздела 5.2.4: Сортировка по объединению. Раздел 5.3.2: Слияние минимального сравнения, стр. 197–207.

внешняя ссылка

• Высокопроизводительная реализация параллельного и последовательного слияния в C # с источником в GitHub И в C ++ GitHub