Фильтр Log Gabor - Log Gabor filter
При обработке сигналов полезно одновременно анализировать пространственные и частотные характеристики сигнала. В то время как преобразование Фурье дает информацию о частоте сигнала, он не локализован. Это означает, что мы не можем определить, какая часть (возможно, длинного) сигнала дает определенную частоту. Можно использовать кратковременное преобразование Фурье для этой цели, однако, кратковременное преобразование Фурье ограничивает базисные функции синусоидальной формой. Для обеспечения более гибкого разложения пространственно-частотного сигнала было предложено несколько фильтров (включая вейвлеты). Лог-Габор[1] filter - один из таких фильтров, который является улучшением оригинального Фильтр Габора.[2] Преимущество этого фильтра перед множеством альтернатив заключается в том, что он лучше соответствует статистике естественных изображений по сравнению с Фильтры Gabor и другие вейвлет фильтры.
Приложения
Фильтр Лог-Габора может описывать сигнал с точки зрения местных частотных характеристик. Поскольку это фундаментальный метод анализа сигналов, он имеет множество применений в обработке сигналов. Действительно, любое приложение, использующее фильтры Габора или другие базовые функции вейвлетов, может извлечь выгоду из фильтра Лог-Габора. Тем не менее, в зависимости от деталей конструкторской проблемы может не быть никакой пользы. Тем не менее, фильтр Лог-Габора оказался особенно полезным в приложениях для обработки изображений, поскольку было показано, что он лучше захватывает статистику естественных изображений.
В обработке изображений есть несколько низкоуровневых примеров использования фильтров Лог-Габора. Обнаружение края - одна из таких примитивных операций, при которой края изображения помечаются. Поскольку края проявляются в частотной области как высокие частоты, естественно использовать фильтр, такой как Log-Gabor, чтобы выделить эти края.[3][4] Эти обнаруженные края могут использоваться в качестве входных данных для алгоритма сегментации или алгоритма распознавания. Связанная проблема - обнаружение угла. При обнаружении углов цель состоит в том, чтобы найти точки на изображении, которые являются углами. Углы полезно находить, потому что они представляют собой устойчивые места, которые можно использовать для проблем сопоставления изображений. Угол может быть описан в терминах информации о локализованной частоте с помощью фильтра Лог-Габора.[5]
В распознавание образов входное изображение должно быть преобразовано в представление объекта, которое упрощает алгоритм классификации для разделения классов. Функции, сформированные из отклика фильтров Лог-Габора, могут образовывать хороший набор функций для некоторых приложений, поскольку они могут локально представлять информацию о частоте. Например, фильтр успешно применялся при классификации выражений лиц.[6] Есть некоторые свидетельства того, что зрительная система человека обрабатывает визуальную информацию аналогичным образом.[7]
Есть множество других приложений, которым требуется локализованная информация о частоте. Фильтр Лог-Габора использовался в таких приложениях, как улучшение изображений,[8] анализ речи,[9] обнаружение контура,[10] синтез текстуры [11] и шумоподавление изображения [12] среди прочего.
Существующие подходы
Существует несколько существующих подходов к вычислению информации о локализованной частоте. Эти подходы выгодны, потому что в отличие от преобразования Фурье эти фильтры могут более легко отображать разрывы в сигнале. Например, преобразование Фурье может представлять край, но только с использованием бесконечного количества синусоидальных волн.
Фильтры Gabor
При рассмотрении фильтров, которые извлекают информацию о локальной частоте, существует взаимосвязь между разрешением по частоте и разрешением во времени / пространстве. Когда берется больше выборок, разрешение частотной информации выше, однако временное / пространственное разрешение будет ниже. Точно так же взятие всего нескольких отсчетов означает более высокое пространственное / временное разрешение, но это происходит за счет меньшего частотного разрешения. Хороший фильтр должен быть в состоянии получить максимальное разрешение по частоте при заданном временном / пространственном разрешении, и наоборот. В Фильтр Габора достигает этой границы.[2] По этой причине фильтр Габора является хорошим методом одновременной локализации пространственной / временной и частотной информации. Фильтр Габора в пространственной (или временной) области формулируется как гауссова огибающая, умноженная на комплексную экспоненту. Было обнаружено, что корковые реакции в зрительной системе человека можно моделировать с помощью фильтра Габора.[7][13] Фильтр Габора был модифицирован Морле для формирования ортонормированного непрерывного вейвлет-преобразования.[14]
Хотя фильтр Габора обеспечивает ощущение оптимальности с точки зрения компромисса между пространством и частотой, в некоторых приложениях он может быть не идеальным фильтром. При определенных полосах пропускания фильтр Габора имеет ненулевую составляющую постоянного тока. Это означает, что реакция фильтра зависит от среднего значения сигнала. Если выходные данные фильтра должны использоваться для приложения, такого как распознавание образов, этот компонент постоянного тока нежелателен, поскольку он дает функцию, которая изменяется со средним значением. Как мы скоро увидим, фильтр Лог-Габора не обнаруживает этой проблемы. Также оригинальный фильтр Габора имеет импульсную характеристику бесконечной длины. Наконец, исходный фильтр Габора, будучи оптимальным с точки зрения неопределенности, не соответствует статистике естественных изображений. Как показано в,[1] в задаче кодирования изображений лучше выбирать фильтр с более длинным наклонным хвостом.
В некоторых приложениях другие разложения имеют преимущества. Хотя существует множество возможных таких разложений, здесь мы кратко представляем два популярных метода: вейвлеты в мексиканской шляпе и управляемая пирамида.
Мексиканская шляпа вейвлет
Рикер вейвлет, обычно называемый мексиканская шляпа вейвлет - еще один тип фильтра, который используется для моделирования данных. Во многих измерениях это становится Лапласиан гауссиана функция. По причинам вычислительной сложности лапласиан гауссовой функции часто упрощается как разница гауссиан. Это различие функции Гаусса нашло применение в нескольких приложениях компьютерного зрения, таких как обнаружение ключевых точек.[15] Недостатком вейвлета мексиканской шляпы является то, что он демонстрирует некоторое наложение спектров и плохо отображает наклонные ориентации.
Управляемая пирамида
В управляемая пирамида разложение [16] был представлен как альтернатива вейвлетам Морлета (Габора) и Рикера. Это разложение игнорирует ограничение ортогональности формулировки вейвлета, и, делая это, можно построить набор фильтров, которые не зависят как от перемещения, так и от вращения. Недостаток разложения управляемой пирамиды состоит в том, что она переполнена. Это означает, что для описания сигнала используется больше фильтров, чем действительно необходимо.
Определение
Филд представил фильтр Лог-Габора и показал, что он может лучше кодировать естественные изображения по сравнению с исходным фильтром Габора.[1] Кроме того, фильтр Лог-Габора не имеет той же проблемы постоянного тока, что и исходный фильтр Габора. Одномерная функция Лог-Габора имеет частотную характеристику:
куда и - параметры фильтра. даст центральную частоту фильтра. влияет на пропускную способность фильтра. При изменении частотного параметра полезно сохранять ту же форму. Для этого соотношение должен оставаться постоянным. На следующем рисунке показана частотная характеристика Gabor по сравнению с Log-Gabor:
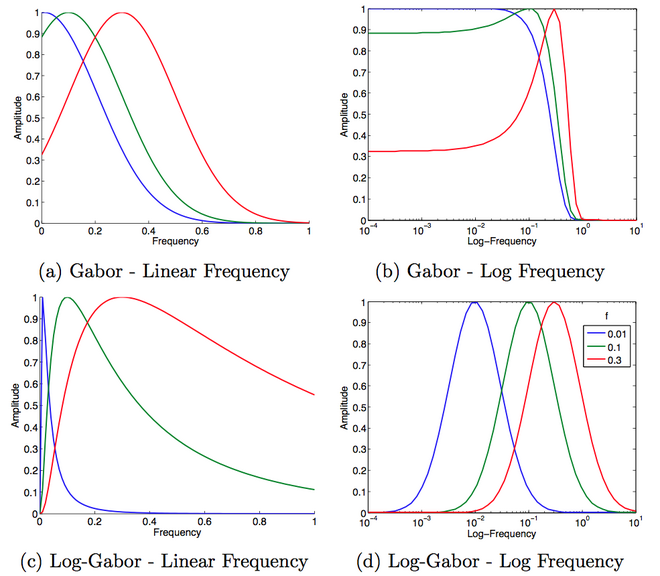
Другое определение фильтра Лог-Габора - рассматривать его как функция распределения вероятностей, с нормальное распределение, но с учетом логарифма частот. Это имеет смысл в тех случаях, когда Закон Вебера – Фехнера применяется, например, в визуальном или слуховом восприятии. Таким образом, после изменения правила переменной одномерная функция Лог-Габора имеет измененную частотную характеристику:
Обратите внимание, что это распространяется на источник и что у нас все еще есть .
В обоих определениях из-за нуля в значении DC невозможно получить аналитическое выражение для фильтра в пространственной области. На практике фильтр сначала проектируется в частотной области, а затем обратное преобразование Фурье дает импульсную характеристику временной области.
Двумерный фильтр Лог-Габора

Как и фильтр Габора, фильтр Лог-Габора пользуется большой популярностью при обработке изображений.[4] По этой причине полезно рассмотреть двумерное расширение фильтра log-Габора. Благодаря этому дополнительному измерению фильтр не только предназначен для определенной частоты, но и для определенной ориентации. Компонент ориентации - это функция расстояния по Гауссу в зависимости от угла в полярных координатах (см. [1] или же [2] ):
где здесь теперь четыре параметра: центральная частота, параметр ширины для частоты, ориентация центра, и параметр ширины ориентации. Пример этого фильтра показан ниже.


Полоса пропускания по частоте определяется как:
Обратите внимание, что результирующая ширина полосы выражается в октавах.
Угловая полоса определяется по формуле:
Во многих практических приложениях набор фильтров предназначен для формирования банк фильтров. Поскольку фильтры не образуют набор ортогональных оснований, конструкция банка фильтров является своего рода искусством и может зависеть от конкретной задачи. Необходимые параметры, которые необходимо выбрать: минимальная и максимальная частоты, ширина полосы фильтра, количество ориентаций, угловая ширина полосы, масштабирование фильтра и количество масштабов.
Смотрите также
- Преобразование Габора
- Вейвлет Габора
- Фильтр Габора
- Атом Габора
- Обнаружение функций (компьютерное зрение) для других детекторов низкоуровневых функций
- Производные изображения
- Снижение шума изображения
- Обнаружение гребня для взаимосвязи между детекторами края и детекторами гребня
Рекомендации
- ^ а б c Д. Дж. Филд. Связь между статистикой естественных изображений и реакционными свойствами корковых клеток. J. Opt. Soc. Являюсь. А, 1987, стр. 2379-2394.
- ^ а б Д. Габор. Теория общения. J. Inst. Электр. Англ. 93, 1946 г.
- ^ З. Сяо, Ч. Го, Ю. Мин и Л. Цян. Исследование вейвлета log Gabor и его применения в обнаружении краев изображений. В Международной конференции по обработке сигналов, том 1, страницы 592–595, август 2002 г.
- ^ а б Сильвен Фишер, Филип Сроубек, Лоран У. Перрине, Рафаэль Редондо, Габриэль Кристобаль. Самообратимые двумерные вейвлеты лог-Габора. Int. Журнал Computational Vision, 2007 г.
- ^ X. Гао, Ф. Саттар и Р. Венкатешварлу. Обнаружение многомасштабных углов изображений с уровнями серого на основе вейвлет-преобразования логарифма Габора. IEEE Transactions on Circuits and Systems for Video Technology, 17 (7): 868–875, июль 2007 г.
- ^ Н. Роуз. Классификация мимики с использованием фильтров Габора и лог-Габора. В Международной конференции по автоматическому распознаванию лиц и жестов (FGR), страницы 346–350, апрель 2006 г.
- ^ а б Дж. Г. Даугман. Отношение неопределенности для разрешения в пространстве, пространственной частоты и ориентации, оптимизированное двумерными визуальными кортикальными фильтрами. Журнал Оптического общества Америки, 1985, стр. 1160-9.
- ^ W. Wang, J. Li, F. Huang и H. Feng. Разработка и реализация фильтра log-Gabor в улучшении изображения отпечатков пальцев. Письма о распознавании образов, 2008. С. 301–308.
- ^ Л. Хе, М. Лех, Н. Мэддейдж и Н. Аллен. Распознавание стресса и эмоций с использованием анализа спектрограмм речи с помощью фильтра Лог-Габора. Аффективные вычисления и интеллектуальное взаимодействие, 2009, стр. 1-6.
- ^ Сильвен Фишер, Рафаэль Редондо, Лоран Перрине, Габриэль Кристобаль. Редкая аппроксимация изображений, вдохновленная функциональной архитектурой основных визуальных областей.. Журнал EURASIP о достижениях в обработке сигналов, специальный выпуск о восприятии изображений, 2007 г.
- ^ Паула С. Леон, Иво Ванцетта, Гийом С. Массон, Лоран У. Перрине. Облака движения: основанный на модели синтез стимулов естественных случайных текстур для изучения восприятия движения. Журнал нейрофизиологии, 107 (11): 3217-3226, 2012
- ^ П. Ковеси. Шумоподавление изображений с сохранением фазы. Конференция Австралийского общества распознавания образов: DICTA’99, 1999, стр. 212–217.
- ^ Эндрю Б. Уотсон. Преобразование коры головного мозга: быстрое вычисление смоделированных нейронных образов. Журнал компьютерного зрения, графики и обработки изображений. 1987. С. 311-327.
- ^ А. Гроссманн и Дж. Морле. Разложение функций Харди на квадратные интегрируемые вейвлеты постоянной формы. Журнал СИАМ по математическому анализу, 1984, стр. 723-736.
- ^ Д. Г. Лоу. Отличительные особенности изображения от масштабно-инвариантные ключевые точки. Международный журнал компьютерного зрения, 2004 г., стр. 91-110.
- ^ Э. П. Симончелли и В. Т. Фриман. Управляемая пирамида: гибкая архитектура для многомасштабных вычислений производных. Международная конференция IEEE по обработке изображений, 1995. С. 444–447.












