Индуктивность утечки - Leakage inductance
Индуктивность утечки происходит из электрических свойств несовершенно связанного трансформатор посредством чего каждый обмотка ведет себя как самоиндукция в серии с соответствующей обмоткой омическое сопротивление постоянный. Эти четыре константы обмотки также взаимодействуют с трансформатором. взаимная индуктивность. Индуктивность рассеяния обмотки возникает из-за того, что поток рассеяния не связан со всеми витками каждой обмотки с несовершенным соединением.
Реактивное сопротивление утечки обычно является наиболее важным элементом трансформатора энергосистемы из-за фактор силы, падение напряжения, Реактивная сила потребление и ток повреждения соображения.[1][2]
Индуктивность утечки зависит от геометрии сердечника и обмоток. Падение напряжения на реактивное сопротивление утечки часто приводит к нежелательному регулированию питания при изменении нагрузки трансформатора. Но это также может быть полезно для гармонический изоляция (ослабление более высокие частоты) некоторых нагрузок.[3]
Индуктивность утечки применима к любому устройству магнитной цепи с несовершенной связью, включая моторы.[4]
Индуктивность утечки и коэффициент индуктивной связи

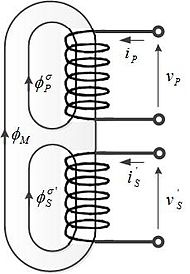
Поток магнитной цепи, который не связывает обе обмотки, представляет собой поток рассеяния, соответствующий индуктивности рассеяния первичной обмотки Lпσ и вторичная индуктивность рассеяния LSσ. Ссылаясь на рис.1, эти индуктивности рассеяния определены в терминах обмотки трансформатора. разомкнутая цепь индуктивности и связанные коэффициент связи или коэффициент связи .[5][6][7]
Самоиндукция разомкнутой первичной цепи определяется выражением
- ------ (Уравнение 1.1a)
где
- ------ (Уравнение 1.1b)
- ------ (Уравнение 1.1c)
и
- первичная самоиндукция
- первичная индуктивность рассеяния
- намагничивающая индуктивность
- коэффициент индуктивной связи
Измерение индуктивности основного трансформатора и коэффициента связи
Собственные индуктивности трансформатора & и взаимная индуктивность являются, в аддитивном и вычитающем последовательном соединении двух обмоток, определяемых формулой[8]
- в аддитивной связи,
- , и,
- в субтрактивной связи,
Коэффициент связи рассчитывается из значения индуктивности, измеренной на одной обмотке при коротком замыкании другой обмотки в соответствии со следующим:[11][12][13]
- За Уравнение 2,7,
- и
- Такой, что
- За Уравнение 2,7,
Мостовая схема Кэмпбелла также может использоваться для определения самоиндукции трансформатора и взаимной индуктивности с использованием переменной стандартной пары взаимных индукторов для одной из сторон моста.[14][15]
Отсюда следует, что самоиндукция холостого хода и коэффициент индуктивной связи даны
- ------ (Ур. 1.2), и,
- , при 0 < < 1 ------ (Уравнение 1.3)
где
и
- взаимная индуктивность
- вторичная самоиндукция
- вторичная индуктивность рассеяния
- индуктивность намагничивания относительно вторичной
- коэффициент индуктивной связи
- это отношение витков
Электрическая достоверность схемы трансформатора на рис. 1 строго зависит от условий холостого хода для соответствующих рассматриваемых индуктивностей обмоток. Более общие условия схемы описаны в следующих двух разделах.
Индуктивный коэффициент утечки и индуктивность
А неидеальный линейный двухобмоточный трансформатор может быть представлен двумя контурами с взаимной индуктивностью, соединяющими пять сопротивление константы, как показано на рис.2.[6][16][17][18]

где
- M - взаимная индуктивность
- & сопротивление первичной и вторичной обмоток
- Константы , , , & измеряются на клеммах трансформатора
- Фактор связи определяется как
- , где 0 < < 1 ------ (Уравнение 2.1)
Соотношение витков обмотки на практике дается как
- ------ (Уравнение 2.2).[19]
где
- Nп & NS витки первичной и вторичной обмоток
- vп & vS и яп и яS напряжения и токи первичной и вторичной обмоток.
Уравнения сетки неидеального трансформатора могут быть выражены следующими уравнениями напряжения и потокосцепления:[20]
- ------ (Уравнение 2.3)
- ------ (Ур. 2.4)
- ------ (Ур. 2.5)
- ------ (Уравнение 2.6),
- где
- это потокосцепление
- является производная потокосцепления по времени.
Эти уравнения могут быть разработаны, чтобы показать, что, если пренебречь соответствующими сопротивлениями обмоток, соотношение индуктивностей цепи обмотки и токов с другой обмоткой закороченный и в испытание на обрыв цепи как следует,[21]
- ------ (Уравнение 2.7),
- где,
Индуктивность трансформатора можно охарактеризовать с помощью трех констант индуктивности следующим образом:[25][26]
- ------ (Уравнение 2.8)
- ------ (Ур. 2.9)
- ------ (Уравнение 2.10) ,
где,

- LM намагничивающая индуктивность, соответствующая намагничивающему сопротивлению XM
- Lпσ & LSσ - первичная и вторичная индуктивности рассеяния, соответствующие первичной и вторичной индуктивности рассеяния Xпσ & ИКСSσ.
Преобразователь можно выразить более удобно как эквивалентная схема на рис.3 с вторичными константами, отнесенными (т. е. с обозначением верхнего индекса) к первичным,[25][26]
- .

поскольку
- ------ (Уравнение 2.11)
и
- ------ (Уравнение 2.12),
у нас есть
- ------ (Уравнение 2.13),
что позволяет выразить эквивалентную схему на рис. 4 через константы рассеяния обмотки и индуктивности намагничивания следующим образом:[26]

- ------ (Ур. 2.14 Уравнение 1.1b)
- ------ (Ур. 2.15 Уравнение 1.1c).
Неидеальный трансформатор на рис. 4 может быть показан как упрощенная эквивалентная схема на рис. 5, с вторичными константами, отнесенными к первичной обмотке, и без идеальной развязки трансформатора, где,
- ------ (Уравнение 2.16)
- ток намагничивания, возбуждаемый потоком ΦM который связывает первичную и вторичную обмотки
- первичный ток
- - вторичный ток, относящийся к первичной обмотке трансформатора.
Уточненный коэффициент индуктивной утечки
Уточненный вывод коэффициента индуктивной утечки
а. По уравнению. 2.1 и IEC IEV 131-12-41 коэффициент индуктивной связи дан кем-то
- --------------------- (Уравнение 2.1):
б. По уравнению. 2.7 и IEC IEV 131-12-42 Коэффициент индуктивной утечки дан кем-то
- ------ (Уравнение 2.7) & (Ур. 3.7a)
c. умножается на дает
- ----------------- (Ур. 3.7b)
d. По уравнению. 2-8 и зная, что
- ---------------------- (Ур. 3.7c)
е. умножается на дает
- ------------------ (Ур. 3.7d)
f. По уравнению. 3.5 Уравнение 1.1b и уравнение. 2.14 и уравнение. 3,6 Уравнение 1.1b и уравнение. 2.14:
- --- (Ур. 3.7e)
Все уравнения в этой статье предполагают, что установившаяся форма сигнала постоянной частоты & значения которых являются безразмерными, фиксированными, конечными и положительными, но меньше 1.
Ссылаясь на диаграмму потока на рис.6, справедливы следующие уравнения:[28][29]
- σп = Φпσ/ ΦM = Lпσ/ ЛM[32] ------ (Ур. 3.1 Уравнение 2.7)
Таким же образом
- σS = ΦSσ '/ ΦM = LSσ '/ ЛM[33] ------ (Ур. 3.2 Уравнение 2.7)
И поэтому,
- Lп = LM + Lпσ = LM + σпLM = (1 + σп) LM[38] ------ (Ур. 3.5 Уравнение 1.1b и уравнение. 2.14)
- LS' = LM + LSσ ' = LM + σSLM = (1 + σS) LM[39] ------ (Ур. 3.6 Уравнение 1.1b и уравнение. 2.14),
где
- σп & σS являются, соответственно, коэффициентом первичной утечки и коэффициентом вторичной утечки.
- ΦM & LM - соответственно взаимный поток и намагничивающая индуктивность
- Φпσ & Lпσ являются, соответственно, первичным потоком рассеяния и первичной индуктивностью рассеяния.
- ΦSσ ' & LSσ ' являются, соответственно, вторичным потоком рассеяния и вторичной индуктивностью рассеяния, которые относятся к первичной.
Таким образом, коэффициент утечки σ может быть уточнен в терминах взаимосвязи указанных выше уравнений индуктивности обмотки и коэффициента индуктивной утечки следующим образом:[40]
- ------ (Ур. От 3.7a до 3.7e).
Приложения
Индуктивность утечки может быть нежелательным свойством, поскольку вызывает изменение напряжения при нагрузке.

Во многих случаях это полезно. Индуктивность утечки имеет полезный эффект ограничения протекания тока в трансформаторе (и нагрузке) без потери мощности (за исключением обычных неидеальных потерь в трансформаторе). Трансформаторы обычно проектируются так, чтобы иметь определенное значение индуктивности рассеяния, так что реактивное сопротивление рассеяния, создаваемое этой индуктивностью, является конкретным значением при желаемой частоте работы. В этом случае реально работающим полезным параметром является не значение индуктивности рассеяния, а индуктивность короткого замыкания ценность.
Коммерческие и распределительные трансформаторы мощностью, скажем, 2500 кВА, обычно проектируются с импедансом короткого замыкания от 3% до 6% и с соответствующим сопротивлением. отношение (отношение реактивного сопротивления обмотки к сопротивлению обмотки) от 3 до 6, которое определяет процентное изменение вторичного напряжения между холостым ходом и полной нагрузкой. Таким образом, для чисто резистивных нагрузок, такие трансформаторы полностью без нагрузки регулирование напряжения будет примерно от 1% до 2%.
Трансформаторы с высоким реактивным сопротивлением утечки используются для некоторых применений с отрицательным сопротивлением, таких как неоновые вывески, где требуется усиление напряжения (действие трансформатора), а также ограничение тока. В этом случае реактивное сопротивление рассеяния обычно составляет 100% от полного сопротивления нагрузки, поэтому даже если трансформатор закорочен, он не будет поврежден. Без индуктивности рассеяния отрицательное сопротивление, характерное для этих газоразрядных ламп, заставило бы их проводить чрезмерный ток и выйти из строя.
Трансформаторы с переменной индуктивностью рассеяния используются для регулирования тока в дуговая сварка наборы. В этих случаях индуктивность рассеяния ограничивает текущий поток до желаемой величины.
Реактивное сопротивление утечки трансформатора играет большую роль в ограничении тока короткого замыкания в пределах максимально допустимого значения в энергосистеме.[2]
Смотрите также
использованная литература
- ^ Ким 1963, п. 1
- ^ а б Саарбафи и Маклин 2014, Руководство по моделированию трансформатора AESO, стр. 9 из 304
- ^ Ирвин 1997, п. 362.
- ^ Пирхёнен, Йокинен и Грабовцова, 2008 г., Глава 4 Утечка флюса
- ^ Термины коэффициент индуктивной связи и коэффициент индуктивной утечки в этой статье определены в Международная электротехническая комиссия Электропедия с ИЭВ-131-12-41, Коэффициент индуктивной связи и ИЭВ-131-12-42, Индуктивный коэффициент утечки.
- ^ а б Бреннер и Джавид 1959, §18-1 Взаимная индуктивность, стр. 587-591.
- ^ IEC 60050 (Дата публикации: 1990-10). Раздел 131-12: Теория схем / Элементы схем и их характеристики, IEV 131-12-41 Коэффициент индуктивной связи
- ^ Бреннер и Джавид 1959, §18-1 Взаимная индуктивность - последовательное соединение взаимной индуктивности, стр. 591-592
- ^ Бреннер и Джавид 1959, стр. 591-592, рис. 18-6.
- ^ Харрис 1952, стр. 723, рис. 43
- ^ Voltech, Измерение индуктивности утечки
- ^ Rhombus Industries, Проверка индуктивности
- ^ Это измерено индуктивность короткого замыкания значение часто называют индуктивностью рассеяния. См., Например, Измерение индуктивности утечки,Тестирование индуктивности. Формальная индуктивность рассеяния определяется выражением (Уравнение 2.14).
- ^ Харрис 1952, стр. 723, рис. 42
- ^ Хурана 2015, стр. 254, рис. 7,33
- ^ Бреннер и Джавид 1959, §18-5 Линейный трансформатор, стр. 595-596
- ^ Хамейер 2001, п. 24
- ^ Сингх 2016, Взаимная индуктивность
- ^ Бреннер и Джавид 1959, §18-6 Идеальный трансформатор, стр. 597-600: Eq. 2.2 выполняется в точности для идеального трансформатора, где, в пределе, когда самоиндуктивность приближается к бесконечному значению ( → ∞ & → ∞) отношение приближается к конечному значению.
- ^ Хамейер 2001, п. 24, ур. 3-1 через ур. 3-4
- ^ Хамейер 2001, п. 25, ур. 3-13
- ^ Ноултон 1949, pp. §8–67, p. 802: Ноултон описывает Фактор утечки как "Полный поток, который проходит через ярмо и входит в полюс = Φм = Φа + Φе и отношение Φм/ Φа называется коэффициентом утечки и превышает 1. «Этот коэффициент, очевидно, отличается от коэффициента индуктивной утечки, описанного в этой статье об индуктивности утечки.
- ^ IEC 60050 (Дата публикации: 1990-10). Раздел 131-12: Теория схем / Элементы схем и их характеристики, IEV исх. 131-12-42: "Коэффициент индуктивной утечки
- ^ IEC 60050 (Дата публикации: 1990-10). Раздел 221-04: Магнитные тела, IEV исх. 221-04-12: "Коэффициент магнитной утечки - отношение общего магнитного потока к полезному магнитному потоку магнитопровода ». Этот коэффициент также отличается от коэффициента индуктивной утечки, описанного в этой статье об индуктивности утечки.
- ^ а б Хамейер 2001, п. 27
- ^ а б c Бреннер и Джавид 1959, §18-7 Эквивалентная схема для неидеального трансформатора, стр. 600-602 и рис. 18–18
- ^ Бреннер и Джавид 1959, п. 602, «Рис. 18-18 В этой эквивалентной схеме (неидеального) трансформатора элементы являются физически реализуемыми, и изоляционные свойства трансформатора сохранены».
- ^ а б Эриксон и Максимович, Глава 12 Основы магнитной теории, §12.2.3. Индуктивность утечки
- ^ Ким 1963, стр. 3-12, Магнитная утечка в трансформаторах; стр. 13-19, Реактивное сопротивление утечки в трансформаторах.
- ^ Хамейер 2001, п. 29, Рис.26
- ^ Ким 1963, п. 4, Рис. 1, Магнитное поле, создаваемое током во внутренней обмотке трансформатора с сердечником; Рис. 2, Магнитное поле, создаваемое током во внешней обмотке на рис. 1.
- ^ Хамейер 2001, стр. 28, ур. 3–31
- ^ Хамейер 2001, стр. 28, ур. 3-32
- ^ Хамейер 2001, стр.29, ур. 3-33
- ^ Ким 1963, п. 10, ур. 12
- ^ Хамейер 2001, стр.29, ур. 3-34
- ^ Ким 1963, п. 10, ур. 13
- ^ Хамейер 2001, стр.29, ур. 3-35
- ^ Хамейер 2001, стр.29, ур. 3-36
- ^ Хамейер 2001, п. 29, ур. 3–37
внешняя ссылка
IEC Электропедия ссылки:
Список используемой литературы
- Бреннер, Эгон; Джавид, Мансур (1959). «Глава 18 - Цепи с магнитной муфтой». Анализ электрических цепей. Макгроу-Хилл. стр. особенно 586–617.CS1 maint: ref = harv (ссылка на сайт)
- Диденко, В .; Сиротин Д. (2012). «Точное измерение сопротивления и индуктивности обмоток трансформатора» (PDF). XX Всемирный конгресс IMEKO - Метрология для зеленого роста. Пусан, Республика Корея, 9−14 сентября 2012 г.CS1 maint: location (ссылка на сайт) CS1 maint: ref = harv (ссылка на сайт)
- Эриксон, Роберт В .; Максимович, Драган (2001). «Глава 12: Основы теории магнетизма (слайды инструктора только для книги)» (PDF). Основы силовой электроники (2-е изд.). Боулдер: Университет Колорадо (слайды) / Спрингер (книга). С. 72 слайда. ISBN 978-0-7923-7270-7.CS1 maint: ref = harv (ссылка на сайт)
- «Электропедия: всемирный электротехнический словарь в Интернете». IEC 60050 (Дата публикации: 1990-10). Архивировано из оригинал 27 апреля 2015 г.
- Хамейер, Кей (2001). Электрические машины I: основы, конструкция, принцип работы, работа (PDF). RWTH Институт электрических машин Ахенского университета. Архивировано из оригинал (PDF) 10 февраля 2013 г.CS1 maint: ref = harv (ссылка на сайт)
- Харрис, Форест К. (1952). Электрические измерения (5-е изд. (1962) изд.). Нью-Йорк, Лондон: Джон Вили и сыновья.CS1 maint: ref = harv (ссылка на сайт)
- Хейланд, А. (1894). "Графический метод прогнозирования силовых трансформаторов и многофазных двигателей". ETZ. 15: 561–564.
- Хейланд, А. (1906). Графическое изображение асинхронного двигателя. Перевод Джорджа Герберта Роу; Рудольф Эмиль Хельмунд. Макгроу-Хилл. С. 48 стр.
- Ирвин, Дж. Д. (1997). Справочник по промышленной электронике. Справочник CRC. Тейлор и Фрэнсис. ISBN 978-0-8493-8343-4.CS1 maint: ref = harv (ссылка на сайт)
- Хурана, Рохит (2015). Электронные приборы и измерения. Издательство Викас. ISBN 9789325990203.CS1 maint: ref = harv (ссылка на сайт)
- Ким, Чжун Чунг (1963). Определение реактивного сопротивления утечки трансформатора с использованием импульсной управляющей функции. 57 страниц: Университет Орегона.CS1 maint: location (ссылка на сайт) CS1 maint: ref = harv (ссылка на сайт)
- Ноултон, A.E., изд. (1949). Стандартное руководство для инженеров-электриков (8-е изд.). Макгроу-Хилл. п. 802, § 8–67: Фактор утечки.CS1 maint: ref = harv (ссылка на сайт)
- МИТ-Пресс (1977). «Само- и взаимные индуктивности». Магнитные цепи и трансформаторы - первый курс для энергетиков и инженеров связи. Кембридж, Массачусетс: MIT-Press. С. 433–466. ISBN 978-0-262-31082-6.CS1 maint: ref = harv (ссылка на сайт)
- Pyrhönen, J .; Йокинен, Т .; Грабовцова, В. (2008). Проектирование вращающихся электрических машин. п. Глава 4 Утечка флюса.CS1 maint: ref = harv (ссылка на сайт)
- «Взаимная индуктивность» (PDF). Rhombus Industries Inc. 1998 г.. Получено 4 августа 2018.CS1 maint: ref = harv (ссылка на сайт)
- Саарбафи, Карим; Маклин, Памела (2014). «Руководство по моделированию трансформатора AESO» (PDF). Калгари: AESO - Оператор электрической системы Альберты (подготовлено Teshmont Consultants LP). стр. 304 стр.. Получено 6 августа, 2018.CS1 maint: ref = harv (ссылка на сайт)
- Сингх, Махендра (2016). «Взаимная индуктивность». Учебники по электронике. Получено 6 января 2017.CS1 maint: ref = harv (ссылка на сайт)
- «Измерение индуктивности утечки» (PDF). Voltech Instruments. 2016 г.. Получено 5 августа 2018.CS1 maint: ref = harv (ссылка на сайт)