Неустойчивость Кельвина – Гельмгольца - Kelvin–Helmholtz instability

Не путать с Механизм Кельвина – Гельмгольца.

Воспроизвести медиа

Численное моделирование временной неустойчивости Кельвина – Гельмгольца.

В Неустойчивость Кельвина – Гельмгольца (после Лорд Кельвин и Герман фон Гельмгольц ) обычно возникает, когда есть сдвиг скорости в единственном сплошная жидкость, или дополнительно там, где существует разница скоростей на границе раздела двух жидкостей. Типичный пример - ветер, дующий над водой, постоянная нестабильности может проявляться через волны на поверхности воды. Неустойчивость Кельвина-Гельмгольца не только ограничивается водной поверхностью в виде облаков, но и проявляется в других природных явлениях, таких как океан, полосы Сатурна, Красное пятно Юпитера, и корона солнца.^[1]

Пространственно развивающаяся 2D неустойчивость Кельвина-Гельмгольца при малых числах Рейнольдса. Небольшие возмущения, накладываемые на входе на касательную скорость, развиваются в вычислительном ящике. Высокое число Рейнольдса будет отмечено увеличением мелкомасштабных движений.

Обзор теории и математические концепции

Нестабильность KH, видимая облаками, известная как флюктус,^[2] над Mount Duval в Австралии

KH нестабильность на планете Сатурн, образовавшаяся при взаимодействии двух полос атмосферы планеты.

Волны Кельвина-Гельмгольца на глубине 500 м в Атлантическом океане

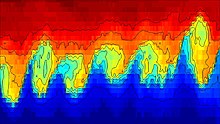
Теория предсказывает наступление нестабильности и переход к турбулентный поток в жидкости разных плотности движется с разной скоростью.^[3] Гельмгольц изучал динамика двух жидкостей разной плотности, когда небольшое возмущение, такое как волна, было введено на границе, соединяющей жидкости. Таким образом, неустойчивость Кельвина-Гельмгольца можно охарактеризовать как неустойчивые мелкомасштабные движения, происходящие в вертикальном и латеральном направлении. Иногда мелкомасштабные нестабильности можно ограничить через предвидение границ. Границы очевидны в вертикальном направлении через верхнюю и нижнюю границы. Верхнюю границу можно рассматривать на примерах как свободную поверхность океана, а нижнюю границу как волну, разбивающуюся о берег.^[4] В латеральном масштабе диффузия и вязкость являются основными факторами рассмотрения, поскольку оба влияют на мелкомасштабные нестабильности. С помощью вышеупомянутого определения нестабильности Кельвина-Гельмгольца различие между неустойчивостью Кельвина-Гельмгольца и мелкомасштабной турбулентностью может быть затруднено. Хотя эти два явления неотделимы друг от друга, Кельвин-Гельмгольц рассматривается как двухмерный феномен по сравнению с турбулентностью, происходящей в трех измерениях.^[4]

В случае короткой длины волны, если не учитывать поверхностное натяжение, две жидкости, движущиеся параллельно с разными скоростями и плотностями, образуют границу раздела, которая нестабильна для всех скоростей. Тем не мение, поверхностное натяжение способен стабилизировать коротковолновую нестабильность и предсказывать стабильность до тех пор, пока не будет достигнут порог скорости. Теория линейной устойчивости, включая поверхностное натяжение, в общих чертах предсказывает начало формирования волн, а также переход к турбулентности в важном случае ветра над водой.^[5]

Недавно было обнаружено, что уравнения жидкости, описывающие линейную динамику системы, допускают четность-временная симметрия, а неустойчивость Кельвина-Гельмгольца возникает тогда и только тогда, когда симметрия четности-времени спонтанно нарушается.^[6]

Для непрерывно меняющегося распределения плотности и скорости (с более легкими слоями вверху, так что жидкость RT-стабильный ) динамика неустойчивости Кельвина-Гельмгольца описывается Уравнение Тейлора – Гольдштейна ${\displaystyle (U-c)[\psi -k^{2}\psi ]+\left[{\frac {N^{2}}{U-c}}-U\right]\psi =0}$ и его начало дается Число Ричардсона ${\displaystyle Ri}$.^[4] Обычно слой нестабилен для ${\displaystyle Ri<0.25}$. Эти эффекты распространены в облачных слоях. Изучение этой неустойчивости применимо в физике плазмы, например в термоядерный синтез с инерционным удержанием и плазма –бериллий интерфейс. Иногда ситуацию, в которой в состоянии статической стабильности, очевидном для более тяжелых жидкостей, находящихся ниже, чем нижняя жидкость, можно пренебречь неустойчивостью Рэлея-Тейлора, поскольку нестабильность Кельвина-Гельмгольца является достаточной при данных условиях.

Понятно, что в случае мелкомасштабной турбулентности увеличение числа Рейнольдса, ${\displaystyle {\displaystyle \mathrm {Re} ={\frac {\rho uD}{\mu }}={\frac {uD}{\nu }}}}$, соответствует увеличению мелкомасштабных движений. Введение числа Рейнольдса сравнимо с введением меры вязкости для отношения, которое ранее определялось как сдвиг скорости и нестабильность. С точки зрения вязкости высокое число Рейнольдса обозначается низкой вязкостью. По сути, высокое число Рейнольдса приводит к увеличению мелкомасштабного движения. Считается, что это мнение соответствует природе нестабильности Кельвина-Гельмгольца.^[7] Показано, что при увеличении числа Рейнольдса в случае неустойчивости Кельвина-Гельмгольца начальные крупномасштабные структуры неустойчивости все еще сохраняются в форме сверхзвуковых форм.^[8]

Численно нестабильность Кельвина-Гельмгольца моделируется во временном или пространственном подходе. При временном подходе экспериментаторы рассматривают течение в периодическом (циклическом) ящике, «движущееся» со средней скоростью (абсолютная неустойчивость). При пространственном подходе экспериментаторы моделируют лабораторный эксперимент с естественными условиями на входе и выходе (конвективная неустойчивость).

Важность и реальные приложения

Явление нестабильности Кельвина-Гельмгольца - это всеобъемлющее явление потока жидкости, которое снова и снова наблюдается в природе. От волн океана до облаков в небе нестабильность Кельвина-Гельмгольца ответственна за некоторые из самых основных структур природы. Дальнейший анализ и моделирование нестабильности Кельвина-Гельмгольца может привести к пониманию природных явлений в мире и многому другому.

Смотрите также

• Неустойчивость Рэлея – Тейлора.
• Неустойчивость Рихтмайера – Мешкова.
• Грибное облако
• Неустойчивость Плато – Рэлея.
• Карман вихревая улица
• Поток Тейлора – Куэтта
• Гидравлическая механика
• Динамика жидкостей
• Число Рейнольдса
• Турбулентность

Примечания

1. Фокс, Карен С. "Обсерватория солнечной динамики НАСА ловит" серферские "волны на Солнце". НАСА-Солнце-Земля: гелиофизика. НАСА.
2. Сазерленд, Скотт (23 марта 2017 г.). «Cloud Atlas переходит в 21 век с 12 новыми типами облаков». Сеть погоды. Пельморекс Медиа. Получено 24 марта 2017.
3. Дразин, П. Г. (2003). Энциклопедия атмосферных наук. Elsevier Ltd. стр. 1068–1072. Дои:10.1016 / B978-0-12-382225-3.00190-0.
4. Грамер, Лью; Gramer @ noaa, Лью; Правительство (27 мая 2007 г.). «Неустойчивости Кельвина-Гельмгольца».
5. FUNADA, T .; ДЖОЗЕФ, Д. (2001-10-25). «Анализ вязкого потенциального течения неустойчивости Кельвина – Гельмгольца в канале». Журнал гидромеханики. 445: 263–283. Дои:10.1017 / S0022112001005572.
6. Цинь, H .; и другие. (2019). «Неустойчивость Кельвина-Гельмгольца является результатом нарушения симметрии четности времени». Физика плазмы. 26 (3): 032102. arXiv:1810.11460. Bibcode:2019PhPl ... 26c2102Q. Дои:10.1063/1.5088498. S2CID  53658729.}
7. Йылмаз, İ; Дэвидсон, L; Эдис, ФО; Сайгин, Х (2011-12-22). «Численное моделирование нестабильности Кельвина-Гельмгольца с использованием неявного недиссипативного алгоритма DNS». Journal of Physics: Серия конференций. 318 (3): 032024. Дои:10.1088/1742-6596/318/3/032024. ISSN  1742-6596.
8. «Неустойчивость Кельвина-Гельмгольца - обзор | Темы ScienceDirect». www.sciencedirect.com. Получено 2020-04-27.

Рекомендации

• Лорд Кельвин (Уильям Томсон) (1871). «Гидрокинетические решения и наблюдения». Философский журнал. 42: 362–377.
• Герман фон Гельмгольц (1868). «Über discontinuierliche Flüssigkeits-Bewegungen [О прерывистых движениях жидкостей]». Monatsberichte der Königlichen Preussische Akademie der Wissenschaften zu Berlin. 23: 215–228.
• Статья, описывающая открытие волн KH в глубоком океане: Броуд, Уильям Дж. (19 апреля 2010 г.). «В глубоком море волны с знакомым завитком». Нью-Йорк Таймс. Получено 23 апреля, 2010.

внешняя ссылка

• Hwang, K.-J .; Гольдштейн; Кузнецова; Ванга; Виньяс; Сибек (2012). «Первое наблюдение на месте волн Кельвина-Гельмгольца на высокоширотной магнитопаузе в условиях сильного восходящего межпланетного магнитного поля». J. Geophys. Res. 117 (A08233): н / д. Bibcode:2012JGRA..117.8233H. Дои:10.1029 / 2011JA017256. HDL:2060/20140009615.
• Гигантские облака в форме цунами катятся по небу Алабамы - Натали Вулховер, Livescience через Yahoo.com
• Облако цунами обрушилось на береговую линию Флориды
• Вихреобразование в свободной струе - Видео на YouTube, показывающее волны Кельвина-Гельмгольца на краю свободной струи, визуализированные в научном эксперименте.
• Волновые облака над Крайстчерч-Сити
• Облака Кельвина-Гельмгольца в Бармуте, Гвинед, 18 февраля 2017 г.