Гибридная теория транспорта фотонов в ткани - Hybrid theory for photon transport in tissue

Гибридная теория за фотон транспорт в тканях использует преимущества и устраняет недостатки как Монте-Карло метод и теория диффузии для переноса фотонов для точного и эффективного моделирования фотонов, проходящих через ткань.

MCML (Монте-Карло моделирование легкого транспорта в многослойной среде)

В MCML представляет собой численный способ моделирования переноса фотонов в биологической ткани. Каждый фотонный пакет следует за случайная прогулка с настойчивостью, где направление каждого шага зависит от направления предыдущего шага. Посредством усреднения нескольких независимых случайных блужданий MCML оценивает усредненные по ансамблю величины, такие как отражательная способность, пропускание, поглощение и плотность энергии.

Вкратце, пакет фотона сначала запускается в биологическую ткань. Параметры переноса фотонов, включая размер шага и угол отклонения из-за рассеяния, определяются путем случайной выборки из распределений вероятностей. Часть веса, определяемая коэффициентами рассеяния и поглощения, откладывается на месте взаимодействия. Пакет фотонов продолжает распространяться, пока оставшийся вес не станет меньше определенного порога. Если этот пакет фотона попадает в границу во время распространения, он либо отражается, либо проходит, что определяется псевдослучайным числом. Для точного получения ожидаемых значений необходимо смоделировать статистически достаточное количество пакетов фотонов.^[1]

Преимущества и недостатки

Этот Метод Монте-Карло строгий и гибкий. Однако из-за своей статистической природы этот метод требует отслеживания большого количества пакетов фотонов, что делает его дорогостоящим в вычислительном отношении.

Теория диффузии

В Теория диффузии представляет собой приближение уравнения переноса излучения (УПИ) и аналитический способ моделирования переноса фотонов. Таким образом, он может быстро моделировать распространение фотонов через ткань.

Например, один из способов получить решение для тонкого пучка, падающего вертикально на полубесконечную однородную рассеивающую среду, состоит в выполнении трех следующих шагов аппроксимации:

• Анизотропно рассеивающая среда превращается в изотропно рассеивающую среду. То есть коэффициент рассеяния масштабируется на ${displaystyle 1-g}$, куда ${displaystyle g}$ - анизотропия. Анизотропия ${displaystyle g}$ затем устанавливается равным нулю;
• Тонкий пучок единичной мощности преобразуется в эквивалентный изотропный точечный источник на глубине, равной транспортной длине свободного пробега, с мощностью, равной транспортному альбедо;
• Граничный эффект рассеивающей среды устраняется путем добавления источника изображения для удовлетворения граничного условия.^[1]

Преимущества и недостатки

Теория диффузии более эффективна с точки зрения вычислений, чем MCML. Однако он также менее точен, чем MCML вблизи источника и границ.

Гибридная теория

Гибридная теория сочетает в себе теорию диффузии и метод Монте-Карло для повышения точности вблизи источника и границ при одновременном сокращении времени вычислений. В предыдущем примере для теории диффузии предполагалась полубесконечная рассеивающая среда только с одной границей. Если геометрия представляет собой плиту, необходимо учитывать вторую границу. Плотность потока энергии на экстраполированных границах должна быть приблизительно 0. Использование массива источников изображения удовлетворяет этому граничному условию. Экстраполированная граница расположена на расстоянии ${displaystyle z_{b}=2C_{R}D}$. В ${displaystyle z}$ координаты исходных пар ${displaystyle z_{pm i}=-z_{b}+2i(d+2z_{b})pm (z'+z_{b})}$ куда ${displaystyle z^{'}}$ это ${displaystyle z}$ координата точечного источника и ${displaystyle d}$ - толщина плиты. Для достижения хорошей точности обычно требуется всего 2-3 пары.

Рисунок 1: Геометрия плиты и пары источников для гибридной теории

Подход Монте-Карло можно использовать для компенсации изначально низкой точности теории диффузии вблизи границ. Как упоминалось ранее, моделирование методом Монте-Карло требует времени. Когда фотонный пакет находится на критической глубине ${displaystyle z_{c}}$ Моделирование Монте-Карло отслеживает все пакеты, но в центральной области пакет фотонов преобразуется в изотропный источник и впоследствии обрабатывается с помощью теории диффузии. Как и в моделировании Монте-Карло, любой переизлучаемый фотонный пакет добавляется к коэффициенту диффузного отражения. ${displaystyle R_{MC}}$.

Когда пакет фотонов рассеивается в центральной зоне ${displaystyle z_{c}leq zleq -z_{c}}$, он условно преобразуется в изотропный точечный источник. Пакет фотонов должен оставаться в центральной области после одной транспортной длины свободного пробега. ${displaystyle l_{t}'}$ вдоль направления распространения пакета фотонов, чтобы он был преобразован в точечный источник, в противном случае моделирование Монте-Карло продолжается. Перед преобразованием в изотропный точечный источник пакет фотонов снижает свой вес из-за его взаимодействия с рассеивающей средой. Полученный вес записывается как исходная функция. ${displaystyle S(r,z)}$. Это накопленное распределение веса, которое можно преобразовать в функцию относительной плотности источника. ${displaystyle S_{d}}$ к:

${displaystyle S_{d}[i_{r},i_{z}]={frac {S[i_{r},i_{z}]}{NDelta V(i_{r})}}}$ куда ${displaystyle Delta V}$ объем сетки и ${displaystyle N}$ - количество пакетов фотонов.

Дополнительное диффузное отражение ${displaystyle R_{DT}}$ из источников рассчитывается как:

${displaystyle R_{DT}(r)=int _{0}^{infty }int _{0}^{infty }int _{0}^{2pi }S_{d}(r',z')R(r,0,0;r',phi ',z')r'dphi 'dr'dz'}$ куда ${displaystyle R}$ из приближения теории диффузии для плиты и ${displaystyle phi }$ азимутальный угол. Общий коэффициент диффузного отражения будет ${displaystyle R_{DT}}$ и ${displaystyle R_{MC}}$ сложены вместе.^[1]

Преимущества перед теорией диффузии и MCML

Существует компромисс между скоростью и точностью моделирования; выбор критической глубины ${displaystyle z_{c}}$ становится решающим фактором для скорости моделирования с большей критической глубиной, что приводит к более медленному времени из-за того, что пакеты должны отслеживаться на более длинном расстоянии до перехода к теории диффузии.^[2]

Преимущества

• Более точен, чем теория диффузии, особенно вблизи источника
• Быстрее, чем метод Монте-Карло

Время использования для метода Монте-Карло (MC) и гибридной модели (H) с использованием IBM ThinkPad T43 с процессором 1,86 ГГц и 1,5 ГБ ОЗУ

${displaystyle n_{rel}}$	${displaystyle d(cm)}$	${displaystyle mu _{a}(cm^{-1})}$	${displaystyle T_{MC}(s)}$	${displaystyle T_{H}(s)}$	${displaystyle T_{MC}(s)/T_{H}(s)}$
1.37	3	0.01	7537	25	301
1.37	3	0.1	4924	25	189
1.37	3	1	1150	25	46
1.37	1	0.01	2600	25	104
1.37	1	0.1	2286	25	91
1.37	1	1	1051	25	41
1	3	0.01	1529	19	80
1	3	0.1	1645	19	87
1	3	1	547	19	29
1	1	0.01	480	19	25
1	1	0.1	480	19	25
1	1	1	442	19	23

Где ${displaystyle n_{rel}}$ - относительный коэффициент преломления, ${displaystyle d}$ толщина плиты, ${displaystyle mu _{a}}$ - коэффициент поглощения, а ${displaystyle T}$ время пользователя.

Сравнение теорий

• 

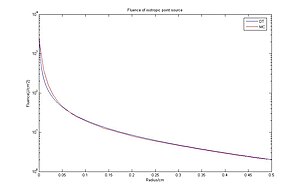
  Сравнение теории диффузии и метода Монте-Карло с точки зрения плотности потока энергии в ответ на изотропный точечный источник.

• 

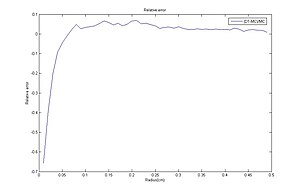
  Относительные ошибки между теорией диффузии и методом Монте-Карло.

• 

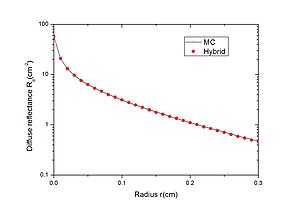
  Сравнение чистого метода Монте-Карло и гибридной модели с точки зрения коэффициента диффузного отражения в ответ на «карандашный» пучок.

• 

  Относительные ошибки между чистым методом Монте-Карло и гибридной моделью.

• 

  Коэффициент диффузного отражения гибридной модели в ответ на карандашный луч, когда критическая глубина установлена ​​на 0,01 см, 0,03 см, 0,05 см и 0,1 см.

• 

  Относительные ошибки с разной критической глубиной для гибридной модели.

• 

  Сравнение метода Монте-Карло и гибридной модели с точки зрения коэффициента диффузного отражения в ответ на карандашный луч, когда критическая глубина установлена ​​на 0,1 см. Коэффициент поглощения ${displaystyle mu _{a}}$ варьируется между 0,1, 1 и 10 ${displaystyle cm^{-1}}$.

Рекомендации

1. LV Wang; Привет Ву (2007). Биомедицинская оптика. Вайли. ISBN  978-0-471-74304-0.
2. Alexandrakis G .; Фаррелл TJ .; Паттерсон М.С. (2000). «Диффузионная гибридная модель Монте-Карло для миграции фотонов в двухслойной мутной среде в частотной области». Прикладная оптика. 39 (13): 2235–2244. Дои:10.1364 / AO.39.002235.