Граф Холта - Holt graph
| Граф Холта | |
|---|---|
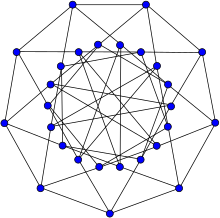 В графе Холта все вершины эквивалентны, и все ребра эквивалентны, но ребра не эквивалентны своим обратным. | |
| Названный в честь | Дерек Ф. Холт |
| Вершины | 27 |
| Края | 54 |
| Радиус | 3 |
| Диаметр | 3 |
| Обхват | 5 |
| Автоморфизмы | 54 |
| Хроматическое число | 3 |
| Хроматический индекс | 5 |
| Толщина книги | 3 |
| Номер очереди | 3 |
| Характеристики | Вершинно-транзитивный Edge-транзитивный Полупереходный Гамильтониан Эйлеров Граф Кэли |
| Таблица графиков и параметров | |
в математический поле теория графов, то Граф Холта или же Граф Дойля самый маленький полупереходный граф, то есть самый маленький пример вершинно-транзитивный и реберно-транзитивный график, который также не симметричный.[1][2] Такие графики встречаются нечасто.[3] Он назван в честь Питера Дж. Дойла и Дерека Ф. Холта, которые независимо открыли тот же граф в 1976 году.[4] и 1981[5] соответственно.
График Холта имеет диаметр 3, радиус 3 и обхват 5, хроматическое число 3, хроматический индекс 5 и является Гамильтониан с 98 472 различными гамильтоновыми циклами.[6] Это также 4-вершинно-связанный и 4-реберный график. Она имеет толщина книги 3 и номер очереди 3.[7]
Имеет группа автоморфизмов автоморфизмов порядка 54.[6] Это меньшая группа, чем симметричный граф с таким же количеством вершин и ребер. График справа подчеркивает это тем, что ему не хватает отражательной симметрии.
Характеристический многочлен графа Холта равен
Галерея

В хроматическое число графа Холта равно 3.

В хроматический индекс графа Холта равно 5.

Граф Холта Гамильтониан.
Рекомендации
- ^ Дойл П. «График с 27 вершинами, который является вершинно-транзитивным и реберно-транзитивным, но не L-транзитивным». Октябрь 1998 г. [1]
- ^ Альспах, Брайан; Марушич, Драган; Новиц, Льюис (1994), «Построение ½-транзитивных графов», Журнал Австралийского математического общества, серия A, 56 (3): 391–402, Дои:10.1017 / S1446788700035564, заархивировано из оригинал на 2003-11-27.
- ^ Джонатан Л. Гросс, Джей Йеллен, Справочник по теории графов, CRC Press, 2004, ISBN 1-58488-090-2, п. 491.
- ^ Дойл, П. Г. (1976), О транзитивных графах, Кандидат медицинских наук, Гарвардский колледж. Цитируется MathWorld.
- ^ Холт, Дерек Ф. (1981), "Граф, который является реберно транзитивным, но не дугово-транзитивным", Журнал теории графов, 5 (2): 201–204, Дои:10.1002 / jgt.3190050210.
- ^ а б Вайсштейн, Эрик В. "Дойл Граф". MathWorld.
- ^ Джессика Вольц, Инженерные линейные схемы с SAT. Магистерская работа, Тюбингенский университет, 2018 г.




