Построение Гольдберга – Кокстера. - Goldberg–Coxeter construction

Многогранник Гольдберга (3,1) и геодезический многогранник (3,1). Многогранники Гольдберга и геодезические многогранники были предшественниками операции Гольдберга-Кокстера.

В Построение Гольдберга – Кокстера. или же Операция Гольдберга – Кокстера (Строительство ГХ или же Работа ГХ) это графическая операция определено на обычный многогранные графы с степень 3 или 4.^[1][2] Это также относится к двойственный граф этих графов, то есть графов с треугольными или четырехугольными «гранями». Конструкцию GC можно рассматривать как подразделение граней многогранника решеткой из треугольных, квадратных или гексагональных многоугольников, возможно, с перекосом относительно исходной грани: это расширение понятий, введенных Многогранники Гольдберга и геодезические многогранники. Конструкция GC в первую очередь изучается в органическая химия для его применения к фуллерены,^[1][2] но это было применено к наночастицы,^[3] системы автоматизированного проектирования,^[4] плетение корзин,^[5][6] и общее изучение теория графов и многогранники.^[7]

Конструкцию Голдберга – Кокстера можно обозначить как ${\displaystyle GC_{k,\ell }(G_{0})}$, куда ${\displaystyle G_{0}}$ график, на котором оперируют, ${\displaystyle k}$ и ${\displaystyle l}$ целые числа, ${\displaystyle k>0}$, и ${\displaystyle \ell \geq 0}$.

История

Майкл Голдберг представил Многогранник Гольдберга в 1937 г.^[8] Бакминстер Фуллер ввел термин "геодезический купол «в 1940-х годах, хотя математику, лежащую в основе куполов, он в основном хранил в секрете.^[9] Геодезические купола - это геометрический двойник (части) многогранника Гольдберга: полный геодезический купол можно рассматривать как геодезический многогранник, двойственный многограннику Гольдберга. В 1962 г. Дональд Каспар и Аарон Клуг опубликовал статью о геометрии вирусные капсиды это применяет и расширяет концепции Голдберга и Фуллера.^[10] H.S.M. Coxeter опубликовал в 1971 году статью, содержащую большую часть той же информации.^[11] Каспар и Клуг были первыми, кто опубликовал наиболее общую правильную конструкцию геодезического многогранника, сделав название «конструкция Гольдберга – Кокстера» примером Закон Стиглера эпонимии.^[12]

Открытие Бакминстерфуллерен в 1985 г. мотивировал исследования других молекул со структурой многогранника Гольдберга. Термины «фуллерен Гольдберга-Кокстера» и «конструкция Гольдберга-Кокстера» были введены Мишель Деза в 2000 г.^[13][14] Это также первый случай рассмотрения дела четвертой степени.

Строительство

Этот раздел во многом следует за двумя статьями Deza et al.^[1][2]

Мастер полигонов

Решетки

n-регулярный	3	4
Домен	Эйзенштейн ${\displaystyle a+bu}$	Гауссовский ${\displaystyle a+bi}$
Примыкает единица измерения	${\displaystyle {\begin{aligned}u&={\frac {1}{2}}\left(1+i{\sqrt {3}}\right)\\&=e^{{\frac {1}{3}}\pi i}=\omega +1\end{aligned}}}$	${\displaystyle i={\sqrt {-1}}}$
Норма ${\displaystyle t(a,b)}$	${\displaystyle a^{2}+ab+b^{2}}$	${\displaystyle a^{2}+b^{2}}$.
Главный многоугольник	${\displaystyle (0,x,xu)}$	${\displaystyle (0,x,x(1+i),xi)}$

Правильные решетки над комплексная плоскость может использоваться для создания «мастер-полигонов». В терминологии геодезических куполов это «структура разрыва» или «главный многогранный треугольник» (PPT). В 4-регулярном случае используется квадратная решетка над Гауссовские целые числа, а в 3-регулярном случае используется треугольная решетка над Целые числа Эйзенштейна. Для удобства используется альтернативная параметризация целых чисел Эйзенштейна, основанная на корне шестой степени из единицы вместо третьего.^[а] Обычное определение целых чисел Эйзенштейна использует элемент ${\textstyle \omega ={\frac {1}{2}}\left(-1+i{\sqrt {3}}\right)=e^{{\frac {2}{3}}\pi i}=u-1}$. Норма, ${\displaystyle t(k,\ell )}$, определяется как квадрат абсолютного значения комплексного числа. Для 3-регулярных графов эта норма является T-число или число триангуляции используется в вирусологии.

Главный многоугольник - это равносторонний треугольник или квадрат, наложенный на решетку. В таблице справа приведены формулы для вершин главных многоугольников в комплексной плоскости, а в галерее ниже показаны главный треугольник и квадрат (3,2). Чтобы многоугольник можно было описать одним комплексным числом, одна вершина имеет фиксированное значение 0. Существует несколько чисел, которые могут описывать один и тот же многоугольник: это соратники друг друга: если ${\displaystyle x}$ и ${\displaystyle y}$ товарищи, то ${\displaystyle x=u^{n}y}$ в Эйзенштейнах или ${\displaystyle x=i^{n}y}$ в гауссианах для некоторого целого числа ${\displaystyle n}$. Набор элементов, связанных друг с другом, представляет собой класс эквивалентности, и элемент каждого класса эквивалентности, имеющий ${\displaystyle a>0}$ и ${\displaystyle b\geq 0}$ это нормальная форма.

• 

  (3,2) главный треугольник над треугольной сеткой

• 

  (3,2) мастер-квадрат над квадратной сеткой

Мастер полигонов и оператор ${\displaystyle GC_{k,\ell }\left(G_{0}\right)}$, можно классифицировать следующим образом:

• Класс I: ${\displaystyle \ell =0.}$
• Класс II: ${\displaystyle k=\ell .}$
• Класс III: все остальные. Операторы класса III существуют в киральных парах: ${\displaystyle GC_{k,\ell }\left(G_{0}\right)}$ киральная пара ${\displaystyle GC_{\ell ,k}(G_{0})}$.

Ниже представлены таблицы главных треугольников и квадратов. Класс I соответствует первому столбцу, а класс II соответствует диагонали с немного более темным фоном.

Мастер полигонов для треугольников

Соедините треугольники через (8,8)
	0	1	2	3	4	5	6	7	8
1
2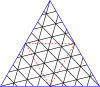
3
4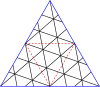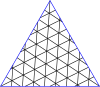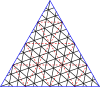
5
6
7
8

Мастер полигонов для квадратов

Мастер-квадраты через (8,8)
	0	1	2	3	4	5	6	7	8
1
2
3
4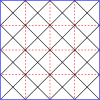
5
6
7
8

Композиция операций Гольдберга – Кокстера соответствует умножению комплексных чисел. Если и только если ${\displaystyle GC_{a,b}\left(GC_{c,d}\left(G_{0}\right)\right)=GC_{e,f}\left(G_{0}\right)}$ (то есть последовательность операций слева дает граф, изоморфный графу справа), то для 3-регулярного графа ${\displaystyle (a+bu)(c+du)}$ находится в классе эквивалентности ${\displaystyle (e+fu)}$, а для 4-регулярного графа ${\displaystyle (a+bi)(c+di)}$ находится в классе эквивалентности ${\displaystyle (e+fi)}$. У этого есть несколько полезных последствий:

• Применение повторных операций Гольдберга – Кокстера коммутативный и ассоциативный.
• Комплексное сопряжение элемента ${\displaystyle a+bi}$ или же ${\displaystyle a+bu}$ соответствует отражению построенного графа.
• Поскольку целые гауссовы и целые евклидовы числа равны Евклидовы области, элементы этих областей могут быть однозначно разложены на простые элементы. Следовательно, также имеет смысл разложить оператор Голдберга – Кокстера на последовательность «простых» операторов Голдберга – Кокстера, и эта последовательность является единственной (с точностью до перестановки).

Выполнение построения ГХ

Этапы выполнения построения GC ${\displaystyle GC_{k,\ell }(G_{0})}$являются следующими:

1. Определите главный многоугольник на основе ${\displaystyle k}$, ${\displaystyle \ell }$, и ${\displaystyle G_{0}}$
2. Если вы работаете с 3- или 4-регулярным графом (вместо графа с треугольными / четырехугольными гранями), возьмите его двойственный граф. Этот двойственный граф будет иметь треугольные или четырехугольные грани.
3. Замените грани триангулированного / четырехугольного графа главным многоугольником. Имейте в виду, что у плоских графов есть «внешняя» грань, которую также необходимо заменить. В приведенном ниже примере это делается путем прикрепления его к одной стороне графика и соединения других сторон по мере необходимости. Это временно вводит перекрывающиеся ребра в граф, но результирующий граф является плоским. Вершины можно переставить так, чтобы не было перекрывающихся ребер.
4. Если исходный граф был 3- или 4-регулярным графом, возьмите двойственный результат шага 3. В противном случае результатом шага 3 будет построение GC.

Ниже приведен пример, где ${\displaystyle GC_{1,1}(G_{0})}$ построен на скелет из куб. На последних двух графиках синие линии - ребра ${\displaystyle G_{0}}$, а черные линии - края ${\displaystyle GC_{1,1}(G_{0})}$. (Пунктирные линии - это нормальные ребра графа, просто нарисованные по-другому, чтобы сделать перекрывающиеся ребра графа более заметными.) Красные вершины находятся в ${\displaystyle G_{0}}$ и оставаться в ${\displaystyle GC_{1,1}(G_{0})}$, в то время как синие вершины создаются заново при построении и находятся только в ${\displaystyle GC_{1,1}(G_{0})}$.

• 

  Мастер-квадрат (1,1)

• 

  Стартовый многогранник (Куб)

• 

  ${\displaystyle G_{0}}$, скелет куба

• 

  Промежуточный этап строительства ${\displaystyle GC_{1,1}(G_{0})}$.

• 

  Результат ${\displaystyle GC_{1,1}(G_{0})}$, после перестановки

• 

  Вложение результата (ромбический додекаэдр )

Расширения

Конструкция Голдберга – Кокстера может быть легко расширена на некоторые неплоские графы, такие как тороидальные графы.^[15] Операторы класса III из-за их киральности требуют графа, который может быть встроенный на ориентируемая поверхность, но операторы классов I и II можно использовать на неориентируемых графах.

Смотрите также

• Геодезическая сетка
• Четырехсторонний сферический куб
• Поверхность подразделения петли
• Подразделение поверхности Катмулла – Кларка
• Обозначения многогранника Конвея

Сноски

1. Это упрощает определение класса эквивалентности, делает определение класса одинаковым для 3- и 4-регулярных графов и соответствует параметризации, традиционно используемой для геодезических куполов и многогранников Голдберга.

Рекомендации

1. Деза, М .; Дютур, М. (2004). «Конструкции Гольдберга – Кокстера для 3- и 4-валентных плоских графов». Электронный журнал комбинаторики. 11: # R20. Дои:10.37236/1773.
2. Деза, М.-М .; Sikirić, M.D .; Штогрин, М. И. (2015). «Построение и параметризация Голдберга – Кокстера». Геометрическая структура химико-релевантных графов: зигзаги и центральные схемы. Springer. С. 131–148. ISBN  9788132224495.
3. Indelicato, G; Буркхард, П; Тварок, Р. (2017). «Классификация самособирающихся архитектур белковых наночастиц для применения в разработке вакцин». Королевское общество открытой науки. 4 (4): 161092. Bibcode:2017RSOS .... 461092I. Дои:10.1098 / rsos.161092. ЧВК  5414263. PMID  28484626.
4. Котани, М; Naito, H; Омори, Т (2017). «Теория дискретных поверхностей». Компьютерный геометрический дизайн. 58: 24–54. Дои:10.1016 / j.cagd.2017.09.002.
5. Тарнаи, Т. (2006). Корзины (PDF). IASS-APCS 2006 Int. Symp. Новая Олимпиада Новая оболочка и пространственные структуры. Пекинский технологический университет: международный доц. для оболочек и пространственных конструкций. стр. IL09.
6. Tarnai, T .; Ковач, Ф .; Fowler, P.W .; Гость, С.Д. (2012). «Обертывание куба и других многогранников». Труды Королевского общества А. 468 (2145): 2652. Bibcode:2012RSPSA.468.2652T. Дои:10.1098 / rspa.2012.0116.
7. Никодим, Диего; Стеглик, Матей (2018). «Упаковка и покрытие нечетных циклов в кубических плоских графах с малыми гранями». Европейский журнал комбинаторики. 67: 208–221. arXiv:1701.07748. Дои:10.1016 / j.ejc.2017.08.004. S2CID  27137740.
8. Гольдберг, М. (1937). «Класс мультисимметричных многогранников». Математический журнал Тохоку.
9. Кеннер, Х. (1976). Геодезическая математика и как ее использовать. Калифорнийский университет Press.
10. Каспар, Д. Л. Д .; Клуг, А. (1962). «Физические принципы построения обычных вирусов». Холодный источник Харб. Symp. Quant. Биол. 27: 1–24. Дои:10.1101 / sqb.1962.027.001.005. PMID  14019094.
11. Кокстер, H.S.M. (1971). «Макромолекулы вирусов и геодезические купола». В Бутчере, J.C. (ред.). Спектр математики. Издательство Оксфордского университета. С. 98–107.
12. Brinkmann, G .; Goetschalckx, P .; Шейн, С. (2017). «Гольдберг, Фуллер, Каспар, Клуг и Кокстер и общий подход к локальным операциям сохранения симметрии». Труды Королевского общества А. 473 (2206): 20170267. arXiv:1705.02848. Bibcode:2017RSPSA.47370267B. Дои:10.1098 / rspa.2017.0267. S2CID  119171258.
13. Деза, М; Fowler, P.W; Рассат, А; Роджерс, К. М. (2000). «Фуллерены как мозаики поверхностей». Журнал химической информации и компьютерных наук. 40 (3): 550–8. CiteSeerX  10.1.1.105.5973. Дои:10.1021 / ci990066h. PMID  10850758.
14. Хирш, Андреас; Чен, Чжунфан; Цзяо, Хайцзюнь (2000). «Сферическая ароматичность в Я Симметричные фуллерены: правило 2 (N + 1) 2 ». Angewandte Chemie. 39 (21): 3915–3917. Дои:10.1002 / 1521-3773 (20001103) 39:21 <3915 :: AID-ANIE3915> 3.0.CO; 2-O. PMID  29711706.
15. Деза, Мишель-Мари; Сикирич, Матье Дютур (2016). «Лего-подобные сферы и торы». Журнал математической химии. 55 (3): 752. Дои:10.1007 / s10910-016-0706-8. S2CID  125087322.