Маятник Фуко - Foucault pendulum

Эта статья про физический эксперимент и реализацию. О романе Умберто Эко см. Маятник Фуко.

Маятник Фуко в Пантеон, Париж

Воспроизвести медиа

Маятник Фуко в COSI Columbus опрокидывать мяч

В Маятник Фуко или же Маятник Фуко это простое устройство, названное в честь французского физика Леон Фуко и задуманный как эксперимент для демонстрации Вращение Земли. В маятник был представлен в 1851 году и был первым экспериментом, который дал простое и прямое свидетельство вращения Земли. Маятники Фуко сегодня популярны в научные музеи и университеты.^[1]

Оригинальный маятник Фуко

Воспроизвести медиа

Маятник Фуко в Пантеоне, Париж

Гравюра с маятником Фуко, 1895 г.

Первая публичная выставка маятника Фуко состоялась в феврале 1851 г. в Меридиане Парижская обсерватория. Несколько недель спустя Фуко сделал свой самый известный маятник, когда подвесил 28-килограммовый (62 фунта) свинец с латунным покрытием. боб проводом длиной 67 метров (220 футов) от купола Пантеон, Париж. Период маятника был ${\displaystyle 2\pi {\sqrt {\frac {l}{g}}}=16.5}$ секунд. Поскольку широта его расположения была ${\displaystyle \phi \,}$ = 48 ° 52 'с.ш., плоскость качания маятника сделала полный круг примерно за ${\displaystyle {\frac {23h56'}{\sin \phi }}}$ = 31,8 часа (31 час 50 минут), вращение по часовой стрелке примерно 11,3 ° в час.

Оригинальный каре, использовавшийся в 1851 году в Пантеоне, был перенесен в 1855 году в Консерватория искусств и ремесел в Париже. Вторая временная установка была сооружена к 50-летию в 1902 году.^[2]

Во время реконструкции музея в 1990-х годах оригинальный маятник был временно выставлен в Пантеоне (1995 г.), но позже был возвращен в музей. Musée des Arts et Métiers до открытия в 2000 году.^[3] 6 апреля 2010 года трос, подвешивающий карабин в Музее искусств и ремесел, оборвался, что нанесло непоправимый ущерб маятниковому карабину и мраморному полу музея.^[4][5] Исходный, теперь поврежденный маятник отображается в отдельном футляре рядом с текущим маятниковым дисплеем.

Точная копия оригинального маятника работает под куполом Пантеона в Париже с 1995 года.^[6]

Объяснение механики

Анимация маятника Фуко в северном полушарии с сильно преувеличенной скоростью вращения Земли. Зеленая кривая показывает путь качания маятника над землей (вращающаяся система отсчета) в любой вертикальной плоскости. Фактическая плоскость поворота кажется вращающейся относительно Земли. Провод должен быть как можно более длинным - обычно длина составляет 12–30 м (40–100 футов).^[7]

В любом Географический Северный полюс или же Географический Южный полюс, плоскость колебания маятника остается неподвижной относительно далекие массы вселенной в то время как Земля вращается под ним, забирая один звездный день для завершения вращения. Таким образом, относительно Земли плоскость колебаний маятника на Северном полюсе, если смотреть сверху, совершает полный оборот по часовой стрелке в течение суток; маятник на Южном полюсе вращается против часовой стрелки.

Когда маятник Фуко подвешен на экватор, плоскость колебаний остается неподвижной относительно Земли. На других широтах плоскость колебаний прецессы относительно Земли, но медленнее, чем на полюсе; угловая скорость, ω (измеряется по часовой стрелке градусы за звездные сутки), пропорционально синус из широта, φ:

${\displaystyle \omega =360^{\circ }\sin \varphi \ /\mathrm {day} }$,

где широты к северу и югу от экватора определены как положительные и отрицательные соответственно. Например, маятник Фуко на 30 ° южной широты, если смотреть сверху наземным наблюдателем, вращается на 360 ° против часовой стрелки за два дня.

Маятник Фуко на Северном полюсе: маятник качается в той же плоскости, что и Земля под ним.

Отрывок из иллюстрированного приложения к журналу Le Petit Parisien датированный 2 ноября 1902 года, к 50-летию эксперимента Леона Фуко, демонстрирующего вращение Земли.

Маятник Фуко требует осторожности при установке, потому что неточная конструкция может вызвать дополнительный поворот, который маскирует земной эффект. Как заметил более поздний нобелевский лауреат Хайке Камерлинг-Оннес, Который разработал более полную теорию маятника Фуко для его докторской диссертации (1879 г.), геометрическое несовершенство системы или упругости опорной проволоки может привести к интерференции между двумя горизонтальными модами колебаний, что привело маятник Оннеса, чтобы перейти от линейного к эллиптическое колебание за час.^[8] Первоначальный запуск маятника также имеет решающее значение; традиционный способ сделать это - использовать пламя, чтобы прожечь нить, которая временно удерживает боб в исходном положении, тем самым избегая нежелательного бокового движения (см. Деталь запуска к 50-летию в 1902 году ).

Примечательно, что отклонение маятника наблюдалось еще в 1661 г. Винченцо Вивиани, ученик Галилео, но нет никаких доказательств того, что он связал эффект с вращением Земли; скорее, он считал это неудобством в своем исследовании, которое следует преодолеть, подвешивая боб на двух веревках вместо одной.

Сопротивление воздуха гасит колебания, поэтому некоторые маятники Фуко в музеях включают в себя электромагнитный или другой привод, чтобы качель качался; другие запускаются регулярно, иногда с церемонией запуска в качестве дополнительной достопримечательности. Помимо сопротивления воздуха, другой главной инженерной проблемой при создании 1-метрового маятника Фуко в настоящее время, как говорят, является обеспечение отсутствия предпочтительного направления качания.^[9]

Анимация описывает движение маятника Фуко на широте 30 ° северной широты. Плоскость колебаний поворачивается на угол -180 ° в течение суток, поэтому через два дня плоскость возвращается в исходную ориентацию.

«Маятниковый день» - это время, необходимое плоскости свободно подвешенного маятника Фуко, чтобы совершить видимый оборот вокруг местной вертикали. Это один звездный день, разделенный на синус широты.^[10][11]

Гироскоп Фуко

Чтобы продемонстрировать вращение прямо, а не косвенно через качающийся маятник, Фуко использовал гироскоп (слово, придуманное Фуко в 1852 году)^[12] в эксперименте 1852 г. Внутренний кардан гироскопа Фуко был уравновешен на ножевых подшипниках на внешнем кардане, а внешний кардан был подвешен на тонкой резьбе без скручивания таким образом, что нижняя точка поворота почти не имела веса. Гироскоп был раскручен до 9000–12000 оборотов в минуту с помощью ряда шестерен перед установкой в ​​нужное положение, что было достаточным временем, чтобы сбалансировать гироскоп и провести 10 минут экспериментов. За прибором можно было наблюдать либо в микроскоп с точностью до десятых долей градуса, либо по длинной стрелке. Еще по крайней мере три копии гироскопа Фуко были изготовлены в удобных дорожных и демонстрационных боксах, а копии сохранились в Великобритании, Франции и США. Гироскоп Фуко стал проблемой и источником вдохновения для таких опытных любителей науки, как Д. Б. Адамсон.^[13]

Прецессия как форма параллельного переноса

Параллельный перенос вектора по замкнутому контуру на сфере: угол, на который он поворачивается, α, пропорциональна площади внутри петли.

В почти инерциальной системе отсчета, движущейся в тандеме с Землей, но не разделяющей вращения Земли вокруг своей оси, точка подвеса маятника проходит по круговой траектории в течение одного звездного дня.

На широте Парижа, 48 градус 51 минута северной широты, полный цикл прецессии занимает чуть менее 32 часов, поэтому после одного звездного дня, когда Земля вернулась в ту же ориентацию, что и предыдущий звездный день, плоскость колебаний повернулась всего на более 270 градусов. Если вначале плоскость поворота была с севера на юг, то на один звездный день позже это будет восток-запад.

Это также означает, что произошел обмен импульс; Земля и качающийся маятник обменялись движением. Земля настолько массивнее маятника, что изменение количества движения Земли незаметно. Тем не менее, поскольку плоскость качания маятника сместилась, законы сохранения подразумевают, что обмен должен был произойти.

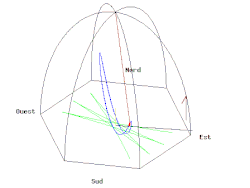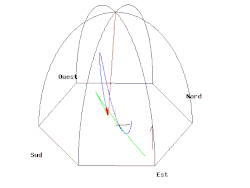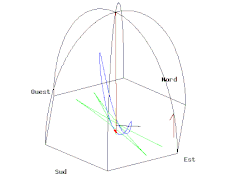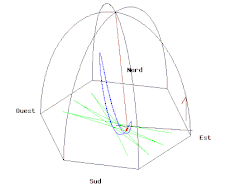
Вместо того, чтобы отслеживать изменение импульса, прецессию плоскости колебаний можно эффективно описать как случай параллельный транспорт. Для этого можно продемонстрировать, составив бесконечно малые вращения, что скорость прецессии пропорциональна проекция из угловая скорость Земли на нормальный направление на Землю, что означает, что след плоскости колебаний претерпит параллельный перенос. Через 24 часа разница между начальной и конечной ориентацией следа в кадре Земли составляет α = −2π грех φ, что соответствует значению, заданному Теорема Гаусса – Бонне. α также называется голономия или же геометрическая фаза маятника. При анализе движений, связанных с землей, рамка Земли не является инерциальная система отсчета, но вращается вокруг местной вертикали с эффективной скоростью 2π грех φ радиан в день. Для описания угла поворота плоскости качания маятника Фуко можно использовать простой метод, использующий параллельный перенос внутри конусов, касательных к поверхности Земли.^[14][15]

С точки зрения привязанной к Земле системы координат с ее Икс- ось, указывающая на восток и ее у-осью, направленной на север, прецессия маятника описывается Сила Кориолиса. Рассмотрим плоский маятник с собственной частотой ω в приближение малых углов. На маятник действуют две силы: восстанавливающая сила, создаваемая силой тяжести и проволоки, и сила Кориолиса. Сила Кориолиса на широте φ горизонтален в приближении малых углов и определяется выражением

${\displaystyle {\begin{aligned}F_{c,x}&=2m\Omega {\dfrac {dy}{dt}}\sin \varphi \\F_{c,y}&=-2m\Omega {\dfrac {dx}{dt}}\sin \varphi \end{aligned}}}$

куда Ω частота вращения Земли, F_c,Икс - составляющая силы Кориолиса в Икс-направление и F_c,у - составляющая силы Кориолиса в у-направление.

Восстанавливающая сила в малоугловое приближение, дан кем-то

${\displaystyle {\begin{aligned}F_{g,x}&=-m\omega ^{2}x\\F_{g,y}&=-m\omega ^{2}y.\end{aligned}}}$

Графики периода прецессии и прецессии за сидерические сутки в зависимости от широты. Знак меняется, когда маятник Фуко вращается против часовой стрелки в Южном полушарии и по часовой стрелке в Северном полушарии. Пример показывает, что один в Париже прецессирует 271 ° каждый звездный день, что занимает 31,8 часа на один оборот.

С помощью Законы движения Ньютона это приводит к системе уравнений

${\displaystyle {\begin{aligned}{\dfrac {d^{2}x}{dt^{2}}}&=-\omega ^{2}x+2\Omega {\dfrac {dy}{dt}}\sin \varphi \\{\dfrac {d^{2}y}{dt^{2}}}&=-\omega ^{2}y-2\Omega {\dfrac {dx}{dt}}\sin \varphi .\end{aligned}}}$

Переход к комплексным координатам z = Икс + иу, уравнения читаются

${\displaystyle {\frac {d^{2}z}{dt^{2}}}+2i\Omega {\frac {dz}{dt}}\sin \varphi +\omega ^{2}z=0\,.}$

Для первого заказа в Ω/ω это уравнение имеет решение

${\displaystyle z=e^{-i\Omega \sin \varphi t}\left(c_{1}e^{i\omega t}+c_{2}e^{-i\omega t}\right)\,.}$

Если время измеряется днями, то Ω = 2π а маятник поворачивается на угол −2π грех φ в течение одного дня.

Связанные физические системы

Устройство, описанное Уитстоном.

Многие физические системы прецессируют аналогично маятнику Фуко. Еще в 1836 году шотландский математик Эдвард Санг придумал и объяснил прецессию прядения верх. В 1851 г. Чарльз Уитстон^[16] описал устройство, которое состоит из вибрирующей пружины, которая установлена ​​на верхней части диска так, что он образует фиксированный угол φ с диском. Пружина ударяется так, что она колеблется в плоскости. Когда диск поворачивается, плоскость колебаний изменяется так же, как и у маятника Фуко на широте. φ.

Аналогичным образом рассмотрим не вращающееся, идеально сбалансированное велосипедное колесо, установленное на диске так, что его ось вращения составляет угол φ с диском. Когда диск совершает полный оборот по часовой стрелке, колесо велосипеда не вернется в исходное положение, а совершит чистый оборот на 2π грех φ.

Прецессия типа Фуко наблюдается в виртуальной системе, в которой безмассовая частица вынуждена оставаться во вращающейся плоскости, наклоненной по отношению к оси вращения.^[17]

Спин релятивистской частицы, движущейся по круговой орбите, прецессирует подобно плоскости качания маятника Фуко. Релятивистское пространство скоростей в Пространство-время Минковского можно рассматривать как сферу S³ в 4-х мерном Евклидово пространство с мнимым радиусом и мнимой времениподобной координатой. Параллельный перенос векторов поляризации вдоль такой сферы приводит к Прецессия Томаса, что аналогично вращению плоскости качания маятника Фуко за счет параллельного переноса по сфере S² в трехмерном евклидовом пространстве.^[18]

В физике эволюция таких систем определяется геометрические фазы.^[19][20] Математически они понимаются через параллельный транспорт.

Маятники Фуко в мире

Дальнейшая информация: Список маятников Фуко

Маятники Фуко можно найти в университетах, научных музеях и т.п. по всему миру. В Объединенные Нации в штаб-квартире в Нью-Йорке есть один; самый большой находится на Конференц-центр Орегона: его длина составляет примерно 27 м (89 футов).^[21][22] Однако раньше маятники были намного длиннее, например, маятник длиной 98 м (322 фута) в Исаакиевский собор, Санкт-Петербург, Россия.^[23][24]

• 

  Маятник Фуко на Musée des Arts et Métiers

• 

  Маятник Фуко на Научный центр Ранчи

• 

  Маятник Фуко на Калифорнийская академия наук

• 

  Маятник Фуко на Девонширский купол, Университет Дерби

Южный полюс

Эксперимент также проводился на Южный полюс, где предполагалось, что вращение Земли будет иметь максимальный эффект^[25][26] на Южнополярная станция Амундсен – Скотт, в шестиэтажном подъезде строящейся новой станции. Маятник имел длину 33 м (108 футов), а боб весил 25 кг (55 фунтов). Расположение было идеальным: никакой движущийся воздух не мог помешать маятнику, а низкая вязкость холодного воздуха уменьшала сопротивление воздуха. Исследователи подтвердили, что период вращения плоскости колебаний составляет около 24 часов.

Смотрите также

• Эффект Кориолиса
• Вращение Земли
• Эксперимент Этвёша
• Инерциальная рамка
• Абсолютное вращение
• Лариат цепочка
• Прецессия

Рекомендации

1. Опря, Джон (1995). «Геометрия и маятник Фуко». Амер. Математика. Ежемесячно. 102 (6): 515–522. Дои:10.2307/2974765. JSTOR  2974765. В архиве из оригинала от 02.04.2015.
2. "Маятник Фуко Пантеона. Церемония инаугурации г-ном Шоме, министром просвещения, сжег трос балансировки, чтобы запустить маятник. 1902". Париж в изображениях. Архивировано из оригинал на 21.08.2014.
3. Киссел, Джо (8 ноября 2004 г.). «Маятник Фуко: низкотехнологичное доказательство вращения Земли». Интересная вещь дня. В архиве из оригинала 12 марта 2012 г.. Получено Двадцать первое марта, 2012.
4. Тиолай, Борис (28 апреля 2010 г.). "Le pendule de Foucault perd la boule". L'Express (На французском). В архиве из оригинала от 10 июля 2010 г.
5. "Маятник Фуко падает на Землю". Times Higher Education. 13 мая 2010 г. В архиве из оригинала 20 марта 2012 г.. Получено Двадцать первое марта, 2012.
6. «Маятник Фуко и парижский пантеон». Атлас-обскура. В архиве с оригинала 12 января 2018 г.. Получено 12 января, 2018.
7. "Маятник Фуко". Смитсоновская энциклопедия. Получено 2 сентября, 2013.
8. Соммерия, Жоэль (1 ноября 2017 г.). «Фуко и вращение Земли». Comptes Rendus Physique. 18 (9): 520–525. Bibcode:2017CRPhy..18..520S. Дои:10.1016 / j.crhy.2017.11.003.
9. "Документ без названия". Архивировано из оригинал 31 марта 2009 г.
10. «Маятниковый день». Глоссарий по метеорологии. Американское метеорологическое общество. Архивировано из оригинал 17 августа 2007 г.
11. Далига, К .; Пржиборски, М .; Шульвич, Дж. «Маятник Фуко. Несложный инструмент в изучении геодезии и картографии». library.iated.org. В архиве из оригинала от 02.03.2016. Получено 2015-11-02.
12. Оксфордский словарь английского языка. VI (2-е изд.). 1989. с. 985.
13. Джули Эванс (2005). Австралийский биографический словарь: Адамсон, Дэвид Беверидж (1823–1891). Национальный центр биографии, Австралийский национальный университет. Получено 28 октября 2020.
14. Сомервилль, В. Б. (1972). «Описание маятника Фуко». Ежеквартальный журнал Королевского астрономического общества. 13: 40. Bibcode:1972QJRAS..13 ... 40S.
15. Харт, Джон Б.; Миллер, Раймонд Э .; Миллс, Роберт Л. (1987). «Простая геометрическая модель для визуализации движения маятника Фуко». Американский журнал физики. 55 (1): 67–70. Bibcode:1987AmJPh..55 ... 67H. Дои:10.1119/1.14972.
16. Чарльз Уитстон Wikisource: "Записка, касающаяся нового механического доказательства вращения Земли М. Фуко. ", стр. 65–68.
17. Бхарадвадж, Правин (2014). «Прецессия Фуко проявляется в простой системе». arXiv:1408.3047 [Physics.pop-ph ].
18. Криворученко, М. И. (2009). «Вращение плоскости качания маятника Фуко и прецессия вращения Томаса: две грани одной монеты». Phys. УСП. 52 (8): 821–829. arXiv:0805.1136. Bibcode:2009PhyU ... 52..821K. Дои:10.3367 / УФНэ.0179.200908е.0873.
19. "Геометрические фазы в физике", ред. Франк Вильчек и Альфред Шапере (World Scientific, Сингапур, 1989).
20. Л. Манджиаротти, Г. Сарданашвили, Калибровочная механика (World Scientific, Сингапур, 1998 г.)
21. «Кристин Джонс - Эндрю Гинзель». Получено 5 мая 2018.
22. «Продукты автоматизации LTW». ltwautomation.net. Архивировано из оригинал 29 апреля 2016 г.. Получено 5 мая 2018.
23. «Первый маятник Фуко в России за полярным кругом». 2018-06-14.
24. Большая Советская Энциклопедия
25. Джонсон, Джордж (24 сентября 2002 г.). «Вот они, 10 самых красивых научных экспериментов». Нью-Йорк Таймс. В архиве с оригинала 31 мая 2012 г.. Получено 20 сентября, 2012.
26. Бейкер, Г. П. (2011). Семь рассказов о маятнике. Oxford University Press. п. 388. ISBN  978-0-19-958951-7.

дальнейшее чтение

• Арнольд, В. (1989). Математические методы классической механики. Springer. п.123. ISBN  978-0-387-96890-2.
• Мэрион, Джерри Б.; Торнтон, Стивен Т. (1995). Классическая динамика частиц и систем (4-е изд.). Брукс Коул. стр.398–401. ISBN  978-0-03-097302-4.
• Перссон, Андерс О. (2005). "Эффект Кориолиса: Четыре века конфликта между здравым смыслом и математикой, Часть I: История до 1885 года" (PDF). История метеорологии. 2. Архивировано из оригинал (PDF) на 2014-04-11. Получено 2006-04-27.

внешняя ссылка

• Рубин, Джулиан (2007). «Изобретение маятника Фуко». Follow the Path of Discovery, 2007, извлечено 31 октября 2007 г. Указания по повторению эксперимента Фуко на сайте любительской науки.
• Вулф, Джо "Вывод прецессии маятника Фуко ".
• "Маятник Фуко ", вывод прецессии в полярных координатах.
• "Маятник Фуко "Автор Джо Вулф, с клипом и анимацией.
• "Маятник Фуко "Йенс-Пер Куска с Джеффом Брайантом, Вольфрам Демонстрационный проект: компьютерная модель маятника, позволяющая управлять частотой маятника, частотой вращения Земли, широтой и временем.
• "Веб-камера Kirchhoff-Institut für Physik, Гейдельбергский университет ".
• Калифорнийская академия наук, Калифорния Объяснение маятника Фуко в удобном формате
• Модель маятника Фуко Экспозиция включает настольное устройство, показывающее эффект Фуко за секунды.
• Фуко, М. Л., Физическая демонстрация вращения Земли с помощью маятника, Институт Франклина, 2000 г., получено 31 октября 2007 г. Перевод его статьи о маятнике Фуко.
• Тобин, Уильям. "Жизнь и наука Леона Фуко".
• Боули, Роджер (2010). «Маятник Фуко». Шестьдесят символов. Брэди Харан за Ноттингемский университет.
• Фуко-Инга Парижбан Маятник Фуко в Париже - видео действующего маятника Фуко в Пантеоне (на венгерском).
• Pendolo nel Salone Маятник Фуко внутри Палаццо делла Раджионе в Падуе, Италия
• Чессин, А.С. (1895). «О маятнике Фуко». Являюсь. J. Math. 17 (1): 81–88. Дои:10.2307/2369710. JSTOR  2369710.
• Макмиллан, Уильям Дункан (1915). «О маятнике Фуко». Являюсь. J. Math. 37 (1): 95–106. Дои:10.2307/2370259. JSTOR  2370259. S2CID  123717776.
• Сомервилль, В. Б. (1972). «Описание маятника Фуко». Q. J. R. Astron. Soc. 13: 40–62. Bibcode:1972QJRAS..13 ... 40S.
• Брагинский, Владимир Б .; Польнарёв Александр Г .; Торн, Кип С. (1984). "Маятник Фуко на Южном полюсе: предложение об эксперименте по обнаружению общего релятивистского гравитомагнитного поля Земли" (PDF). Phys. Rev. Lett. 53 (9): 863. Bibcode:1984ПхРвЛ..53..863Б. Дои:10.1103 / PhysRevLett.53.863.
• Крейн, Х. Ричард (1995). Настенные часы "Маятник Фуко""". Являюсь. J. Phys. 63 (1): 33–39. Bibcode:1995AmJPh..63 ... 33C. Дои:10.1119/1.17765.
• Hard, John B .; Миллер, Раймонд Э. (1987). «Простая геометрическая модель для визуализации движения маятника Фуко». Являюсь. J. Phys. 55 (1): 67. Bibcode:1987AmJPh..55 ... 67H. Дои:10.1119/1.14972.
• Das, U .; Талукдар, Б .; Шаманна, Дж. (2002). «Косвенное аналитическое представление маятника Фуко». Чехослова. J. Phys. 52 (12): 1321–1327. Bibcode:2002CzJPh..52.1321D. Дои:10.1023 / А: 1021819627736.
• Salva, Horacio R .; Benavides, Rubén E .; Перес, Хулио С .; Cuscueta, Диего Дж. (2010). «Маятник Фуко». Rev. Sci. Instrum. 81 (11): 115102–115102–4. Bibcode:2010RScI ... 81k5102S. Дои:10.1063/1.3494611. PMID  21133496.
• Далига, К .; Пржиборски, М .; Шульвич, Дж. (2015). «Маятник Фуко. Несложный инструмент в изучении геодезии и картографии». EDULEARN15 Proceedings - 7-я Международная конференция по образованию и новым технологиям обучения, Барселона, Испания. ISBN  978-84-606-8243-1.