Справедливость (машинное обучение) - Fairness (machine learning)

В машинное обучение, данный алгоритм как говорят справедливый, или иметь справедливость, если его результаты не зависят от заданных переменные, особенно те, которые считаются чувствительными, например, черты личности, которые не должны коррелировать с результатом (например, пол, этническая принадлежность, сексуальная ориентация, инвалидность и т. д.).

Контекст

Исследования справедливости в машинном обучении - относительно недавняя тема. Большинство статей об этом написано за последние три года.^[1] Вот некоторые из наиболее важных фактов в этой теме:

• В 2018 году IBM представила AI Fairness 360, Python библиотека с несколькими алгоритмами для сокращения ПО предвзятость и повысить его справедливость.^[2][3]
• В 2018 году Facebook обнародовал использование инструмента Fairness Flow для выявления предвзятости в их ИИ. Тем не менее исходный код инструмента недоступен, и неизвестно, действительно ли он исправляет предвзятость.^[4]
• В 2019 году Google опубликовал набор инструментов в GitHub изучить влияние справедливости в долгосрочной перспективе.^[5]

Споры

Алгоритмы, используемые для обеспечения справедливости, все еще совершенствуются. Однако главный прогресс в этой области заключается в том, что некоторые крупные корпорации осознают влияние, которое алгоритмический уклон мог повлиять на общество.

Пример спорного использования алгоритма является то, как Facebook размещает новостные статьи для пользователей, которые некоторые люди жаловались могут ввести политические предубеждения. Перед выборами некоторые кандидаты пытались использовать Facebook для агитационных целей, что может стать предметом горячих споров.

Прозрачность алгоритмов

Многие люди жаловались, что алгоритмы часто невозможно проверить, чтобы убедиться, что они работают честно, что не может нанести ущерб некоторым пользователям.

Но многие коммерческие компании предпочитают не раскрывать детали используемых ими алгоритмов, поскольку они часто заявляют, что это может помочь конкурирующим компаниям получить выгоду от их технологий.

Подразумеваемое

Если алгоритм не работает должным образом, последствия для людей могут быть значительными и долгосрочными, например, в отношении возможностей получения образования или трудоустройства, а также доступа к услугам финансового кредита.

Международные стандарты

Поскольку алгоритмы постоянно меняются и часто являются частными, существует несколько признанных стандартов для их построения или работы.

Со временем алгоритмы могут стать более строго регулируемыми, но в настоящее время за ними мало общественного контроля.

Критерии справедливости в задачах классификации^[6]

В классификация задачи, алгоритм изучает функцию предсказания дискретной характеристики ${\textstyle Y}$, целевая переменная, из известных характеристик ${\textstyle X}$. Мы моделируем ${\textstyle A}$ как дискретный случайная переменная который кодирует некоторые характеристики, содержащиеся или неявно закодированные в ${\textstyle X}$ которые мы считаем чувствительными характеристиками (пол, этническая принадлежность, сексуальная ориентация и т. д.). Окончательно обозначим через ${\textstyle R}$ предсказание классификатор.Теперь давайте определим три основных критерия для оценки того, является ли данный классификатор справедливым, то есть, не влияют ли на его прогнозы некоторые из этих чувствительных переменных.

Независимость

Мы говорим случайные переменные ${\textstyle (R,A)}$ удовлетворить независимость если чувствительные характеристики ${\textstyle A}$ находятся статистически независимый к предсказанию ${\textstyle R}$, и мы пишем ${\textstyle R\bot A}$.

Мы также можем выразить это понятие следующей формулой:

$${\displaystyle P(R=r|A=a)=P(R=r|A=b)\quad \forall r\in R\quad \forall a,b\in A}$$

Это означает, что вероятность Классификация алгоритмом в каждой из групп одинакова для двух индивидов с разными чувствительными характеристиками.

Еще одно эквивалентное выражение независимости может быть дано с использованием концепции взаимная информация между случайные переменные, определяется как

$${\displaystyle I(X,Y)=H(X)+H(Y)-H(X,Y)}$$

В этой формуле ${\textstyle H}$ из случайная переменная. потом ${\textstyle (R,A)}$ удовлетворить независимость, если ${\textstyle H(R,A)=0}$.

Возможный расслабление определения независимости включают введение положительного слабина ${\textstyle \epsilon >0}$ и задается формулой:${\displaystyle P(R=r|A=a)\geq P(R=r|A=b)-\epsilon \quad \forall r\in R\quad \forall a,b\in A}$

Наконец, еще один возможный расслабление требует ${\textstyle I(R,A)\leq \epsilon }$.

Разделение

Мы говорим случайные переменные ${\textstyle (R,A,Y)}$ удовлетворить разделение если чувствительные характеристики ${\textstyle A}$ находятся статистически независимый к предсказанию ${\textstyle R}$ с учетом целевого значения ${\textstyle Y}$, и мы пишем ${\textstyle R\bot A|Y}$.

Мы также можем выразить это понятие следующей формулой:

$${\displaystyle P(R=r|Y=q,A=a)=P(R=r|Y=q,A=b)\quad \forall r\in R\quad q\in Y\quad \forall a,b\in A}$$

Это означает, что вероятность Классификация с помощью алгоритма в каждой из групп одинакова для двух людей с разными чувствительными характеристиками, учитывая, что они фактически принадлежат к одной группе (имеют одинаковую целевую переменную).

Другое эквивалентное выражение в случае двоичной целевой ставки: истинно положительная ставка и ложноположительный рейтинг равны (и, следовательно, ложноотрицательная ставка и истинно отрицательная ставка равны) для каждого значения чувствительных характеристик:

$${\displaystyle P(R=1|Y=1,A=a)=P(R=1|Y=1,A=b)\quad \forall a,b\in A}$$

$${\displaystyle P(R=1|Y=0,A=a)=P(R=1|Y=0,A=b)\quad \forall a,b\in A}$$

Наконец, еще одно возможное ослабление данных определений - позволить разнице между ставками быть положительное число ниже заданного слабина ${\textstyle \epsilon >0}$, а не равным нулю.

Достаточность

Мы говорим случайные переменные ${\textstyle (R,A,Y)}$ удовлетворить достаточность если чувствительные характеристики ${\textstyle A}$ находятся статистически независимый к целевому значению ${\textstyle Y}$ учитывая прогноз ${\textstyle R}$, и мы пишем ${\textstyle Y\bot A|R}$.

Мы также можем выразить это понятие следующей формулой:

$${\displaystyle P(Y=q|R=r,A=a)=P(Y=q|R=r,A=b)\quad \forall q\in Y\quad r\in R\quad \forall a,b\in A}$$

Это означает, что вероятность Фактическое нахождение в каждой из групп одинаково для двух людей с разными чувствительными характеристиками, учитывая, что они были предсказаны как принадлежащие к одной и той же группе.

Связь между определениями

Наконец, мы суммируем некоторые из основных результатов, которые связаны с тремя приведенными выше определениями:

• Если ${\textstyle A}$ и ${\textstyle Y}$ не статистически независимый, то достаточность и независимость не могут выполняться одновременно.
• Предполагая ${\textstyle Y}$ является двоичным, если ${\textstyle A}$ и ${\textstyle Y}$ не статистически независимый, и ${\textstyle R}$ и ${\textstyle Y}$ не статистически независимый в любом случае независимость и разделение не могут иметь места одновременно.
• Если ${\textstyle (R,A,Y)}$ как совместное распределение имеет положительный вероятность для всех возможных значений и ${\textstyle A}$ и ${\textstyle Y}$ не статистически независимый, то разделение и достаточность не могут выполняться одновременно.

Метрики^[7]

Большинство статистических показателей справедливости основаны на разных показателях, поэтому мы начнем с их определения. При работе с двоичный классификатора, как прогнозируемый, так и фактический классы могут принимать два значения: положительное и отрицательное. Теперь давайте начнем объяснять различные возможные отношения между прогнозируемым и фактическим результатом:

Матрица путаницы

• Истинно положительный (TP): Случай, когда и прогнозируемый, и фактический результат относятся к положительному классу.
• Истинно отрицательный (TN): Случай, когда прогнозируемый и фактический исход относятся к отрицательному классу.
• Ложноположительный результат (FP): Случай, который, по прогнозам, попадет в положительный класс, приписанный в фактическом исходе к отрицательному.
• Ложноотрицательный (FN): Случай, согласно прогнозам, относящийся к отрицательному классу с фактическим исходом, относится к положительному.

Эти отношения легко представить в виде матрица путаницы, таблица, описывающая точность модели классификации. В этой матрице столбцы и строки представляют экземпляры прогнозируемого и фактического случаев соответственно.

Используя эти отношения, мы можем определить несколько показателей, которые позже можно будет использовать для измерения справедливости алгоритма:

• Положительное прогнозируемое значение (PPV): доля положительных случаев, которые были правильно предсказаны, из всех положительных прогнозов. Обычно его называют точность, и представляет вероятность правильного положительного прогноза. Он задается следующей формулой:

$${\displaystyle PPV=P(actual=+|prediction=+)={\frac {TP}{TP+FP}}}$$

• Коэффициент ложного обнаружения (FDR): доля положительных прогнозов, которые были фактически отрицательными, среди всех положительных прогнозов. Он представляет собой вероятность ошибочного положительного прогноза, который определяется следующей формулой:

$${\displaystyle FDR=P(actual=-|prediction=+)={\frac {FP}{TP+FP}}}$$

• Отрицательное прогнозируемое значение (NPV): доля отрицательных случаев, которые были правильно предсказаны, среди всех отрицательных прогнозов. Он представляет собой вероятность правильного отрицательного прогноза, и он дается следующей формулой:

$${\displaystyle NPV=P(actual=-|prediction=-)={\frac {TN}{TN+FN}}}$$

• Уровень ложных пропусков (FOR): доля отрицательных прогнозов, которые были фактически положительными, из всех отрицательных прогнозов. Он представляет собой вероятность ошибочного отрицательного прогноза, который определяется следующей формулой:

$${\displaystyle FOR=P(actual=+|prediction=-)={\frac {FN}{TN+FN}}}$$

• Истинно положительная ставка (TPR): доля положительных случаев, которые были правильно предсказаны, из всех положительных случаев. Обычно это называют чувствительностью или отзывом, и он представляет собой вероятность положительных предметов, которые следует правильно классифицировать как таковые. Он задается формулой:

$${\displaystyle TPR=P(prediction=+|actual=+)={\frac {TP}{TP+FN}}}$$

• Ложноотрицательная ставка (FNR): доля положительных случаев, которые были неверно предсказаны как отрицательные, из всех положительных случаев. Он представляет собой вероятность положительных предметов неправильно отнести к отрицательным, и это задается формулой:

$${\displaystyle FNR=P(prediction=-|actual=+)={\frac {FN}{TP+FN}}}$$

• Истинно отрицательная ставка (TNR): доля правильно предсказанных отрицательных случаев из всех отрицательных случаев. Он представляет собой вероятность отрицательных предметов следует правильно классифицировать как таковые, и это задается формулой:

$${\displaystyle TNR=P(prediction=-|actual=-)={\frac {TN}{TN+FP}}}$$

• Уровень ложных срабатываний (FPR): доля отрицательных случаев, которые были неверно предсказаны как положительные, из всех отрицательных случаев. Он представляет собой вероятность отрицательных предметов неправильно отнести к положительным, и это задается формулой:

$${\displaystyle FPR=P(prediction=+|actual=-)={\frac {FP}{TN+FP}}}$$

Другие критерии справедливости

Взаимосвязь между критериями справедливости, как показано в Barocas et al.^[6]

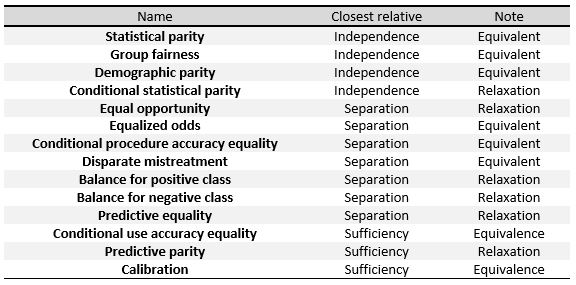
Следующие критерии можно понимать как меры трех определений, данных в первом разделе, или как их ослабление. В таблице^[6] справа мы видим отношения между ними.

Чтобы определить эти меры конкретно, мы разделим их на три большие группы, как это сделано в Verma et al:^[7] определения, основанные на прогнозируемом результате, на прогнозируемых и фактических результатах, и определения, основанные на прогнозируемых вероятностях и фактическом результате.

Мы будем работать с двоичным классификатором и следующей нотацией: ${\textstyle S}$ относится к баллу, присвоенному классификатором, который представляет собой вероятность того, что определенный предмет находится в положительном или отрицательном классе.${\textstyle R}$ представляет собой окончательную классификацию, предсказанную алгоритмом, и ее значение обычно выводится из ${\textstyle S}$, например, будет положительным, когда ${\textstyle S}$ выше определенного порога.${\textstyle Y}$ представляет собой фактический результат, то есть реальную классификацию человека и, наконец, ${\textstyle A}$ обозначает чувствительные атрибуты субъектов.

Определения, основанные на прогнозируемом результате

Определения в этом разделе сосредоточены на прогнозируемом результате. ${\textstyle R}$ для различных распределения предметов. Это самые простые и интуитивно понятные представления о справедливости.

• Групповая справедливость, также называемый статистический паритет, демографический паритет, Скорость принятия и сравнительный анализ. Классификатор удовлетворяет этому определению, если субъекты в защищенных и незащищенных группах имеют равную вероятность быть отнесенными к положительному предсказанному классу. Это если выполняется следующая формула:

$${\displaystyle P(R=+|A=a)=P(R=+|A=b)\quad \forall a,b\in A}$$

• Условная статистическая четность. В основном состоит в приведенном выше определении, но ограничивается только подмножество атрибутов. В математической записи это будет:

$${\displaystyle P(R=+|L=l,A=a)=P(R=+|L=l,A=b)\quad \forall a,b\in A\quad \forall l\in L}$$

Определения, основанные на прогнозируемых и фактических результатах

Эти определения учитывают не только прогнозируемый результат. ${\textstyle R}$ но также сравните это с фактическим результатом ${\textstyle Y}$.

• Прогнозирующая четность, также называемый результат теста. Классификатор удовлетворяет этому определению, если субъекты в защищенных и незащищенных группах имеют одинаковую PPV. Это если выполняется следующая формула:

$${\displaystyle P(Y=+|R=+,A=a)=P(Y=+|R=+,A=b)\quad \forall a,b\in A}$$

Математически, если классификатор имеет одинаковый PPV для обеих групп, он также будет иметь одинаковый FDR, удовлетворяющий формуле:

$${\displaystyle P(Y=-|R=+,A=a)=P(Y=-|R=+,A=b)\quad \forall a,b\in A}$$

• Ложноположительный баланс частоты ошибок, также называемый прогнозируемое равенство. Классификатор удовлетворяет этому определению, если субъекты в защищенных и незащищенных группах имеют водные FPR. Это если выполняется следующая формула:

$${\displaystyle P(R=+|Y=-,A=a)=P(R=+|Y=-,A=b)\quad \forall a,b\in A}$$

Математически, если классификатор имеет равную FPR для обеих групп, он также будет иметь равное TNR, удовлетворяющее формуле:

$${\displaystyle P(R=-|Y=-,A=a)=P(R=-|Y=-,A=b)\quad \forall a,b\in A}$$

• Ложноотрицательный баланс коэффициента ошибок, также называемый равные возможности. Классификатор удовлетворяет этому определению, если субъекты в защищенных и незащищенных группах имеют равное FNR. Это если выполняется следующая формула:

$${\displaystyle P(R=-|Y=+,A=a)=P(R=-|Y=+,A=b)\quad \forall a,b\in A}$$

Математически, если классификатор имеет равное FNR для обеих групп, ti также будет иметь равный TPR, удовлетворяющий формуле:

$${\displaystyle P(R=+|Y=+,A=a)=P(R=+|Y=+,A=b)\quad \forall a,b\in A}$$

• Уравненные шансы, также называемый равенство точности условных процедур и несопоставимое плохое обращение. Классификатор удовлетворяет этому определению, если субъекты в защищенной и незащищенной группах имеют равный TPR и равный FPR, удовлетворяющий формуле:

$${\displaystyle P(R=+|Y=y,A=a)=P(R=+|Y=y,A=b)\quad y\in \{+,-\}\quad \forall a,b\in A}$$

• Условное равенство точности использования. Классификатор удовлетворяет этому определению, если субъекты в защищенной и незащищенной группах имеют равные PPV и равные NPV, удовлетворяющие формуле:

$${\displaystyle P(Y=y|R=y,A=a)=P(Y=y|R=y,A=b)\quad y\in \{+,-\}\quad \forall a,b\in A}$$

• Общее равенство точности. Классификатор удовлетворяет этому определению, если субъект в защищенной и незащищенной группах имеет одинаковую точность предсказания, то есть вероятность того, что объект из одного класса будет отнесен к нему. Это если он удовлетворяет следующей формуле:

$${\displaystyle P(R=Y,A=a)=P(R=Y|A=b)\quad \forall a,b\in A}$$

• Равенство обращения. Классификатор удовлетворяет этому определению, если субъекты в защищенной и незащищенной группах имеют равное соотношение FN и FP, удовлетворяющее формуле:

$${\displaystyle {\frac {FN_{A=a}}{FP_{A=a}}}={\frac {FN_{A=b}}{FP_{A=b}}}}$$

Определения, основанные на прогнозируемых вероятностях и фактическом результате

Эти определения основаны на фактическом результате ${\textstyle Y}$ и прогнозируемая оценка вероятности ${\textstyle S}$.

• Тест-честность, также известный как калибровка или же согласование условных частот. Классификатор удовлетворяет этому определению, если люди с одинаковой оценкой вероятности ${\textstyle S}$ имеют одинаковую вероятность быть отнесены к положительному классу, когда они принадлежат либо к защищенной, либо к незащищенной группе:

$${\displaystyle P(Y=+|S=s,A=a)=P(Y=+|S=s,A=b)\quad \forall s\in S\quad \forall a,b\in A}$$

• Хорошая калибровка является расширением предыдущего определения. В нем говорится, что когда люди внутри или вне защищенной группы имеют одинаковый прогнозируемый показатель вероятности ${\textstyle S}$ они должны иметь одинаковую вероятность быть отнесенными к положительному классу, и эта вероятность должна быть равна ${\textstyle S}$:

$${\displaystyle P(Y=+|S=s,A=a)=P(Y=+|S=s,A=b)=s\quad \forall s\in S\quad \forall a,b\in A}$$

• Баланс для положительного класса. Классификатор удовлетворяет этому определению, если субъекты, составляющие положительный класс из защищенных и незащищенных групп, имеют одинаковый средний прогнозируемый показатель вероятности. ${\textstyle S}$. Это означает, что ожидаемое значение вероятностной оценки для защищенных и незащищенных групп с положительным фактическим результатом ${\textstyle Y}$ то же самое, удовлетворяющее формуле:

$${\displaystyle E(S|Y=+,A=a)=E(S|Y=+,A=b)\quad \forall a,b\in A}$$

• Остаток по отрицательному классу. Классификатор удовлетворяет этому определению, если субъекты, составляющие негативный класс из защищенных и незащищенных групп, имеют равную среднюю прогнозируемую оценку вероятности. ${\textstyle S}$. Это означает, что ожидаемое значение вероятностной оценки для защищенных и незащищенных групп с отрицательным фактическим результатом ${\textstyle Y}$ то же самое, удовлетворяющее формуле:

$${\displaystyle E(S|Y=-,A=a)=E(S|Y=-,A=b)\quad \forall a,b\in A}$$

Алгоритмы

Справедливость может применяться к алгоритмам машинного обучения тремя разными способами: предварительная обработка данных, оптимизация во время обучения программного обеспечения или после обработки результатов алгоритма.

Предварительная обработка

Обычно проблема не только в классификаторе; в набор данных тоже предвзято. Дискриминация набора данных ${\textstyle D}$ по отношению к группе ${\textstyle A=a}$ можно определить следующим образом:

$${\displaystyle disc_{A=a}(D)={\frac {|\{X\in D|X(A)\neq a,X(Y)=+\}|}{|\{X\in D|X(A)\neq a\}|}}-{\frac {|\{X\in D|X(A)=a,X(Y)=+\}|}{|\{X\in D|X(A)=a\}|}}}$$

То есть приближение к разнице между вероятностями принадлежности к положительному классу при условии, что субъект имеет защищенную характеристику, отличную от ${\textstyle a}$ и равно ${\textstyle a}$.

Алгоритмы, исправляющие систематическую ошибку при предварительной обработке, удаляют информацию о переменных набора данных, которая может привести к несправедливым решениям, при этом стараясь изменить как можно меньше. Это не так просто, как просто удалить чувствительную переменную, потому что другие атрибуты могут быть соотнесены с защищенной.

Один из способов сделать это - сопоставить каждого человека в исходном наборе данных с промежуточным представлением, в котором невозможно определить, принадлежит ли он к определенной защищенной группе, сохраняя при этом как можно больше информации. Затем новое представление данных корректируется для достижения максимальной точности алгоритма.

Таким образом, индивидуумы отображаются в новом многовариантном представлении, где вероятность того, что любой член защищенной группы будет отображен на определенное значение в новом представлении, такая же, как вероятность индивидуума, который не принадлежит к защищенной группе. . Затем это представление используется для получения прогноза для человека вместо исходных данных. Поскольку промежуточное представление конструируется с одинаковой вероятностью для лиц внутри или вне защищенной группы, этот атрибут скрыт для классификатора.

Пример объяснен в Zemel et al.^[8] где полиномиальный^{[необходимо разрешение неоднозначности ]} случайная величина используется как промежуточное представление. При этом системе рекомендуется сохранять всю информацию, кроме той, которая может привести к необъективным решениям, и получать как можно более точные прогнозы.

С одной стороны, эта процедура имеет то преимущество, что предварительно обработанные данные можно использовать для любой задачи машинного обучения. Кроме того, нет необходимости изменять классификатор, поскольку поправка применяется к набор данных перед обработкой. С другой стороны, другие методы дают лучшие результаты по точности и справедливости.^[9]

Повторное взвешивание^[10]

Повторное взвешивание - это пример алгоритма предварительной обработки. Идея состоит в том, чтобы присвоить вес каждой точке набора данных, чтобы взвешенные дискриминация равен 0 по отношению к указанной группе.

Если набор данных ${\textstyle D}$ была беспристрастна чувствительная переменная ${\textstyle A}$ и целевая переменная ${\textstyle Y}$ было бы статистически независимый и вероятность совместное распределение будет произведением вероятностей следующим образом:

$${\displaystyle P_{exp}(A=a\wedge Y=+)=P(A=a)\times P(Y=+)={\frac {|\{X\in D|X(A)=a\}|}{|D|}}\times {\frac {|\{X\in D|X(Y)=+\}|}{|D|}}}$$

В действительности, однако, набор данных не является беспристрастным, и переменные не являются статистически независимый Таким образом, наблюдаемая вероятность равна:

$${\displaystyle P_{obs}(A=a\wedge Y=+)={\frac {|\{X\in D|X(A)=a\wedge X(Y)=+\}|}{|D|}}}$$

Чтобы компенсировать предвзятость, программное обеспечение добавляет масса, ниже для избранных объектов и выше для нежелательных объектов. Для каждого ${\textstyle X\in D}$ мы получили:

$${\displaystyle W(X)={\frac {P_{exp}(A=X(A)\wedge Y=X(Y))}{P_{obs}(A=X(A)\wedge Y=X(Y))}}}$$

Когда у нас есть для каждого ${\textstyle X}$ вес связанный ${\textstyle W(X)}$ мы вычисляем взвешенную дискриминацию относительно группы ${\textstyle A=a}$ следующее:

$${\displaystyle disc_{A=a}(D)={\frac {\sum W(X)X\in \{X\in D|X(A)\neq a,X(Y)=+\}}{\sum W(X)X\in \{X\in D|X(A)\neq a\}}}-{\frac {\sum W(X)X\in \{X\in D|X(A)=a,X(Y)=+\}}{\sum W(X)X\in \{X\in D|X(A)=a\}}}}$$

Можно показать, что после повторного взвешивания эта взвешенная дискриминация равна 0.

Оптимизация во время обучения

Другой подход - исправить предвзятость во время тренировки. Это можно сделать, добавив ограничения к цели оптимизации алгоритма.^[11] Эти ограничения вынуждают алгоритм повышать справедливость, сохраняя одинаковые уровни определенных мер для защищенной группы и остальных лиц. Например, мы можем добавить к цели алгоритм условие, что частота ложных срабатываний одинакова для лиц в защищенной группе и для лиц вне защищенной группы.

Основными показателями, используемыми в этом подходе, являются частота ложных срабатываний, частота ложных отрицательных результатов и общий уровень ошибочной классификации. К цели алгоритма можно добавить только одно или несколько из этих ограничений. Обратите внимание, что равенство ложноотрицательных показателей подразумевает равенство истинно положительных показателей, поэтому это подразумевает равенство возможностей. После добавления ограничений проблема может стать неразрешимой, поэтому может потребоваться их ослабление.

Этот метод дает хорошие результаты в улучшении справедливости при сохранении высокой точности и позволяет программист выберите меры справедливости для улучшения. Однако для каждой задачи машинного обучения может потребоваться применение разных методов, а также необходимо изменить код в классификаторе, что не всегда возможно.^[9]

Состязательное ослабление^[12][13]

Мы тренируем двоих классификаторы в то же время с помощью некоторого градиентного метода (например: градиентный спуск ). Первый, предсказатель пытается выполнить задачу прогнозирования ${\textstyle Y}$, целевая переменная, заданная ${\textstyle X}$, вход, изменяя его веса ${\textstyle W}$ чтобы свести к минимуму некоторые функция потерь ${\textstyle L_{P}({\hat {y}},y)}$. Второй, противник пытается выполнить задачу прогнозирования ${\textstyle A}$, чувствительная переменная, заданная ${\textstyle {\hat {Y}}}$ путем изменения его веса ${\textstyle U}$ чтобы минимизировать некоторую функцию потерь ${\textstyle L_{A}({\hat {a}},a)}$.

Важным моментом здесь является то, что для правильного размножения ${\textstyle {\hat {Y}}}$ указанное выше должно относиться к необработанному результату классификатора, а не к дискретному прогнозу; например, с искусственная нейронная сеть и проблема классификации, ${\textstyle {\hat {Y}}}$ может относиться к выходу слой softmax.

Затем мы обновляем ${\textstyle U}$ минимизировать ${\textstyle L_{A}}$ на каждом этапе обучения согласно градиент ${\textstyle \nabla _{U}L_{A}}$ и мы модифицируем ${\textstyle W}$ согласно выражению:

$${\displaystyle \nabla _{W}L_{P}-proj_{\nabla _{W}L_{A}}\nabla _{W}L_{P}-\alpha \nabla _{W}L_{A}}$$

куда $\alpha$ настраиваемый гиперпараметр которые могут меняться на каждом временном шаге.

Графическое представление векторов, используемых в противодействии сглаживанию, как показано в Zhan et al.^[12]

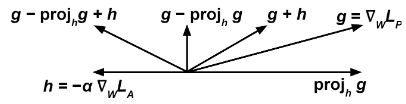
Интуитивно понятная идея состоит в том, что мы хотим предсказатель попытаться свести к минимуму ${\textstyle L_{P}}$ (поэтому термин ${\textstyle \nabla _{W}L_{P}}$), в то же время максимизируя ${\textstyle L_{A}}$ (поэтому термин ${\textstyle -\alpha \nabla _{W}L_{A}}$), таким образом противник не может предсказать чувствительную переменную из ${\textstyle {\hat {Y}}}$.

Период, термин ${\textstyle -proj_{\nabla _{W}L_{A}}\nabla _{W}L_{P}}$ предотвращает предсказатель от движения в направлении, которое помогает противник уменьшить его функцию потерь.

Можно показать, что обучение предсказатель модель классификации с этим алгоритмом улучшает демографический паритет в отношении обучения без противник.

Постобработка

Последний метод пытается исправить результаты классификатора для достижения справедливости. В этом методе у нас есть классификатор, который возвращает оценку для каждого человека, и нам нужно сделать для них двоичное прогнозирование. Высокие баллы могут дать положительный результат, а низкие - отрицательные, но мы можем скорректировать порог чтобы определить, когда следует ответить «да» по желанию. Обратите внимание, что вариации порогового значения влияют на компромисс между коэффициентами истинно положительных и истинно отрицательных результатов.

Если функция оценки справедлива в том смысле, что она не зависит от защищенного атрибута, то любой выбор порога также будет справедливым, но классификаторы этого типа имеют тенденцию быть предвзятыми, поэтому для каждой защищенной группы может потребоваться другой порог. чтобы добиться справедливости.^[14] Один из способов сделать это - построить график зависимости истинно положительной частоты от ложноотрицательной при различных настройках порога (это называется кривой ROC) и найти порог, при котором показатели для защищенной группы и других лиц равны.^[14]

Преимущества постобработки заключаются в том, что метод может применяться после любых классификаторов, не изменяя его, и имеет хорошие показатели по показателям справедливости. Минусы - необходимость доступа к защищенному атрибуту во время тестирования и отсутствие выбора баланса между точностью и справедливостью.^[9]

Отклонить классификацию на основе опционов^[15]

Учитывая классификатор позволять ${\textstyle P(+|X)}$ быть вероятностью, вычисленной классификаторами как вероятность что экземпляр ${\textstyle X}$ принадлежит к положительному классу +. Когда ${\textstyle P(+|X)}$ близко к 1 или к 0, экземпляр ${\textstyle X}$ определено с высокой степенью уверенности для принадлежности к классу + или - соответственно. Однако когда ${\textstyle P(+|X)}$ чем ближе к 0,5, тем сложнее классификация.

Мы говорим ${\textstyle X}$ "отклоненный экземпляр", если ${\textstyle max(P(+|X),1-P(+|X))\leq \theta }$ с определенным ${\textstyle \theta }$ такой, что ${\textstyle 0.5<\theta <1}$.

Алгоритм "ROC" состоит в классификации неотбракованных экземпляров в соответствии с приведенным выше правилом и отклоненных экземпляров следующим образом: если экземпляр является примером лишенной группы (${\displaystyle X(A)=a}$), затем пометьте его как положительный, в противном случае - как отрицательный.

Мы можем оптимизировать различные меры дискриминация (ссылка) как функции ${\textstyle \theta }$ найти оптимальный ${\textstyle \theta }$ по каждой проблеме и избегайте дискриминации привилегированной группы.^[15]

Смотрите также

• Алгоритмический уклон
• Машинное обучение

Рекомендации

1. Мориц Хардт, Беркли. Проверено 18 декабря 2019 г.
2. «Набор инструментов с открытым исходным кодом IBM AI Fairness 360 добавляет новые функции». Tech Republic.
3. IBM AI Fairness 360. Проверено 18 декабря 2019 г.
4. Fairness Flow - детектор сообщений Facebook. Проверено 28 декабря 2019 г.
5. ML-Fairness тренажерный зал. Проверено 18 декабря 2019 г.
6. Солон Барокас; Мориц Хардт; Арвинд Нараянан, Справедливость и машинное обучение. Проверено 15 декабря 2019.
7. Сахил Верма; Юлия Рубин, Объяснение определений справедливости. Проверено 15 декабря 2019 г.
8. Ричард Земель; Ю (Леделл) Ву; Кевин Сверски; Тониан Питасси; Синтия Дворк, Обучение ярмарке представлений. Дата обращения 1 декабря 2019.
9. Цзыюань Чжун, Учебник по справедливости в машинном обучении. Дата обращения 1 декабря 2019.
10. Фейсал Камиран; Мульт Колдерс, Методы предварительной обработки данных для классификации без дискриминации. Проверено 17 декабря 2019 г.
11. Мухаммад Билал Зафар; Изабель Валера; Мануэль Гомес Родригес; Кришна П. Гуммади, Справедливость за пределами разрозненного обращения и разрозненного воздействия: классификация обучения без несоизмеримого жестокого обращения. Дата обращения 1 декабря 2019.
12. Брайан Ху Чжан; Блейк Лемуан; Маргарет Митчелл, Снижение нежелательных предубеждений с помощью состязательного обучения. Проверено 17 декабря 2019 г.
13. Джойс Сюй, Алгоритмические решения алгоритмической предвзятости: техническое руководство. Проверено 17 декабря 2019 г.
14. Мориц Хардт; Эрик Прайс; Натан Сребро, Равенство возможностей в обучении с учителем. Дата обращения 1 декабря 2019.
15. Фейсал Камиран; Асим Карим; Сянлян Чжан, Теория принятия решений для классификации с учетом дискриминации. Проверено 17 декабря 2019 г.