Ансамблевое прогнозирование - Ensemble forecasting

Вершина: Модель исследования и прогнозирования погоды моделирование следов урагана Рита. Нижний: Распространение Национальный центр ураганов многомодельный ансамблевой прогноз.

Ансамблевое прогнозирование метод, используемый в или внутри численный прогноз погоды. Вместо того, чтобы делать один прогноз наиболее вероятной погоды, составляется набор (или ансамбль) прогнозов. Этот набор прогнозов направлен на то, чтобы указать диапазон возможных будущих состояний атмосферы. Ансамблевое прогнозирование - это форма Анализ Монте-Карло. Множественное моделирование проводится для учета двух обычных источников неуверенность в моделях прогноза: (1) ошибки, вызванные использованием несовершенных начальных условий, усиленные хаотичный природа уравнений эволюции атмосферы, которую часто называют чувствительная зависимость от начальных условий; и (2) ошибки, возникшие из-за недостатков в формулировке модели, такие как приближенные математические методы решения уравнений. В идеале подтвержденное будущее состояние атмосферы должно находиться в пределах прогнозируемого ансамбля. распространять, а величина разброса должна быть связана с неопределенностью (ошибкой) прогноза. В целом этот подход может использоваться для вероятностного прогноза любых динамическая система, и не только для прогнозов погоды.

Сегодня ансамблевые прогнозы обычно делаются на большинстве основных средств оперативного прогнозирования погоды по всему миру, включая:

Экспериментальные ансамблевые прогнозы делаются в ряде университетов, таких как Вашингтонский университет, а ансамблевые прогнозы в США также генерируются ВМС США и Воздушные силы. Существуют различные способы просмотра данных, например спагетти, ансамбль означает или же Почтовые марки где можно сравнить ряд различных результатов прогона моделей.

История

Смотрите также: История численного прогноза погоды

По предложению Эдвард Лоренц в 1963 году для долгосрочных прогнозов, сделанных более чем на две недели вперед, невозможно предсказать состояние атмосферы с любой степенью точности. навык благодаря хаотическая природа из динамика жидкостей вовлеченные уравнения.[1] Кроме того, существующие сети наблюдений имеют ограниченное пространственное и временное разрешение (например, над большими водоемами, такими как Тихий океан), что вносит неопределенность в истинное начальное состояние атмосферы. Хотя система уравнений, известная как Уравнения Лиувилля, существует для определения начальной неопределенности при инициализации модели, уравнения слишком сложны, чтобы работать в реальном времени, даже с использованием суперкомпьютеров.[2] Практическая важность ансамблевых прогнозов проистекает из того факта, что в хаотической и, следовательно, нелинейной системе скорость роста ошибки прогноза зависит от начальных условий. Таким образом, ансамблевый прогноз обеспечивает предварительную оценку предсказуемости, зависящей от состояния, то есть оценку типов погоды, которые могут произойти, с учетом неизбежных неопределенностей в начальных условиях прогноза и точности вычислительного представления уравнений. Эти неопределенности ограничивают точность модели прогноза примерно шестью днями в будущем.[3] Первые оперативные ансамблевые прогнозы были составлены для субсезонных временных шкал в 1985 году.[4] Однако стало понятно, что философия, лежащая в основе таких прогнозов, актуальна и в более коротких временных масштабах - временных масштабах, в которых прогнозы ранее делались чисто детерминированными средствами.

Эдвард Эпштейн признал в 1969 г., что атмосфера не может быть полностью описана с помощью одного прогона прогноза из-за неотъемлемой неопределенности, и предложил стохастический динамическая модель, которая произвела средства и отклонения для состояния атмосферы.[5] Хотя эти Моделирование Монте-Карло показал мастерство, в 1974 г. Сесил Лейт выяснилось, что они дают адекватные прогнозы только тогда, когда ансамбль распределение вероятностей была репрезентативной выборкой вероятностного распределения в атмосфере.[6] Только в 1992 г. ансамблевые прогнозы начали готовить Европейский центр среднесрочных прогнозов погоды (ЕЦСПП) и Национальные центры экологического прогнозирования (NCEP).

Методы представления неопределенности

При составлении ансамблевого прогноза погоды необходимо учитывать два основных источника неопределенности: неопределенность начальных условий и неопределенность модели.[7]

Неопределенность начального состояния

Неопределенность начальных условий возникает из-за ошибок в оценке начальных условий для прогноза, как из-за ограниченных наблюдений за атмосферой, так и из-за неопределенностей, связанных с использованием косвенных измерений, таких как спутниковые данные, для измерения состояния атмосферных переменных. Неопределенность начальных условий представлена ​​нарушением начальных условий между различными элементами ансамбля. Это исследует диапазон начальных условий, соответствующих нашим знаниям о текущем состоянии атмосферы, а также ее прошлой эволюции. Есть несколько способов генерировать эти возмущения начальных условий. Модель ECMWF, Система ансамблевого прогнозирования (EPS),[8] использует комбинацию сингулярные векторы и ансамбль ассимиляции данных (EDA) для моделирования начального плотность вероятности.[9] Возмущения сингулярного вектора более активны во внетропиках, а возмущения EDA более активны в тропиках. Ансамбль NCEP, Глобальная система ансамблевого прогнозирования, использует метод, известный как векторное разведение.[10][11]

Неопределенность модели

Неопределенность модели возникает из-за ограничений модели прогноза. Процесс представления атмосферы в компьютерной модели включает множество упрощений, таких как разработка параметризация схемы, которые вносят ошибки в прогноз. Было предложено несколько методов для представления неопределенности модели.

Схемы возмущенных параметров

При разработке параметризация В схеме введено много новых параметров для представления упрощенных физических процессов. Эти параметры могут быть очень неопределенными. Например, 'увлечение коэффициент 'представляет собой бурный смешивание сухого воздуха окружающей среды в конвективное облако, и поэтому представляет собой сложный физический процесс с использованием одного числа. В подходе с возмущенными параметрами неопределенные параметры в схемах параметризации модели идентифицируются, и их значение изменяется между членами ансамбля. При вероятностном моделировании климата, например Climateprediction.net, эти параметры часто остаются постоянными глобально и на протяжении всей интеграции,[12] в современных численных прогнозах погоды более распространено стохастическое изменение значений параметров во времени и пространстве.[13] Степень отклонения параметра можно определить, используя экспертную оценку,[14] или путем прямой оценки степени неопределенности параметра для данной модели.[15]

Стохастические параметризации

Традиционный параметризация Схема направлена ​​на представление среднего воздействия субсеточного движения (например, конвективных облаков) на разрешенное состояние масштаба (например, крупномасштабные поля температуры и ветра). Схема стохастической параметризации признает, что может быть много состояний масштаба подсетки, согласующихся с конкретным состоянием разрешенного масштаба. Вместо прогнозирования наиболее вероятного движения в масштабе подсетки схема стохастической параметризации представляет одну возможную реализацию подсетки. Это достигается за счет включения случайные числа в уравнения движения. Это образцы из распределение вероятностей отнесены к неопределенным процессам. Стохастическая параметризация значительно улучшила навыки моделей прогнозирования погоды и теперь используется в центрах оперативного прогнозирования по всему миру.[16] Стохастические параметризации были впервые разработаны в Европейский центр среднесрочных прогнозов погоды.[17]

Мультимодельные ансамбли

Когда для создания прогноза используется множество различных моделей прогноза, этот подход называется прогнозированием с использованием нескольких моделей ансамбля. Этот метод прогнозирования может улучшить прогнозы по сравнению с подходом на основе одной модели.[18] Когда модели в многомодельном ансамбле корректируются с учетом их различных смещений, этот процесс известен как «суперсамблевое прогнозирование». Этот тип прогноза значительно снижает количество ошибок в выходных данных модели.[19] Когда комбинируются модели различных физических процессов, такие как комбинации моделей атмосферы, океана и волн, многомодельный ансамбль называется гипер-ансамблем.[20]

Оценка вероятности

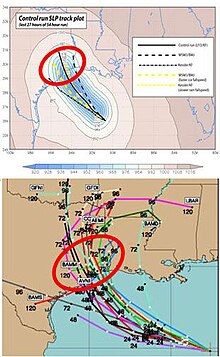
Ансамблевый прогноз обычно оценивается путем сравнения среднего значения отдельных прогнозов для одной переменной прогноза с наблюдаемым значением этой переменной («ошибка»). Это сочетается с учетом степени согласия между различными прогнозами в рамках ансамблевой системы, что представлено их общими прогнозами. стандартное отклонение или "распространение". Разброс ансамбля можно визуализировать с помощью таких инструментов, как спагетти-диаграммы, которые показывают разброс одной величины на прогностических диаграммах для определенных временных шагов в будущем. Еще один инструмент, в котором используется ансамблевое распространение, - это метеограмма, который показывает разброс прогноза одной величины для одного конкретного местоположения. Обычно разброс по ансамблю слишком мал, так что наблюдаемое состояние атмосферы выходит за рамки ансамблевого прогноза. Это может привести к чрезмерной уверенности прогнозиста в своем прогнозе.[21] Эта проблема становится особенно серьезной для прогнозов погоды примерно на 10 дней вперед,[22] особенно если в прогнозе не учитывается неопределенность модели.

Надежность и разрешающая способность (калибровка и резкость)

Разброс ансамблевого прогноза показывает, насколько уверенным может быть прогнозист в своем прогнозе. Когда разброс ансамбля невелик, а решения прогнозов согласованы в рамках нескольких прогонов модели, прогнозисты воспринимают прогноз в целом с большей уверенностью.[21] Когда разброс большой, это указывает на большую неопределенность в прогнозе. В идеале отношения распространения навыков должен существовать, при этом разброс ансамбля является хорошим предиктором ожидаемой ошибки в среднем ансамбле. Если прогноз надежный, наблюдаемое состояние будет вести себя так, как если бы оно было получено из распределения вероятностей прогноза. Надежность (или калибровка) можно оценить путем сравнения стандартного отклонения ошибки в среднем по ансамблю с разбросом прогноза: для надежного прогноза они должны совпадать как в разное время выполнения прогноза, так и для разных мест.[23]

Также можно оценить надежность прогнозов конкретного погодного явления. Например, если 30 из 50 членов указали на количество осадков более 1 см в течение следующих 24 часов, вероятность превышения 1 см можно оценить как 60%. Прогноз будет считаться надежным, если, учитывая все прошлые ситуации, когда прогнозировалась 60% -ная вероятность, в 60% этих случаев количество осадков действительно превышало 1 см. На практике вероятности, полученные из оперативных ансамблевых прогнозов погоды, не обладают высокой надежностью, хотя с набором прошлых прогнозов (пересматривает или же ретроспективные прогнозы) и наблюдения, оценки вероятности из ансамбля могут быть скорректированы для обеспечения большей надежности.

Еще одно желаемое свойство ансамблевых прогнозов - это разрешающая способность. Это показатель того, насколько прогноз отклоняется от частоты климатологических событий - при условии, что ансамбль надежен, увеличение этого отклонения повысит полезность прогноза. Это качество прогноза также можно рассматривать с точки зрения Острота, или насколько мал разброс прогноза. Ключевой целью синоптика должно быть максимальное повышение резкости при сохранении надежности.[24] Прогнозы с большими шагами неизбежно не будут особенно точными (с особенно высоким разрешением), поскольку неизбежные (хотя обычно небольшие) ошибки в начальных условиях будут расти с увеличением опережения прогноза до тех пор, пока ожидаемая разница между двумя состояниями модели не станет такой же большой, как разница между двумя случайными состояниями из климатологии модели прогноза.

Калибровка ансамблевых прогнозов

Если ансамблевые прогнозы должны использоваться для прогнозирования вероятностей наблюдаемых погодных переменных, они обычно нуждаются в калибровке для создания объективных и надежных прогнозов. Для прогнозов температуры существует один простой и эффективный метод калибровки. линейная регрессия, часто известный в этом контексте как Статистика вывода модели. Модель линейной регрессии принимает среднее по ансамблю в качестве предиктора реальной температуры, игнорирует распределение членов ансамбля вокруг среднего и предсказывает вероятности, используя распределение остатков из регрессии. В этой настройке калибровки значение ансамбля в улучшении прогноза состоит в том, что среднее по ансамблю обычно дает лучший прогноз, чем любой отдельный член ансамбля, и не из-за какой-либо информации, содержащейся в ширине или форме распределения элементов в ансамбль вокруг среднего. Однако в 2004 году обобщение линейной регрессии (теперь известное как Неоднородная гауссова регрессия ) был представлен[25] который использует линейное преобразование ансамблевого разброса, чтобы дать ширину прогнозирующего распределения, и было показано, что это может привести к прогнозам с более высокой квалификацией, чем те, которые основаны только на линейной регрессии. Это впервые доказало, что информация в виде распределения членов ансамбля вокруг среднего, в данном случае суммированного разбросом ансамбля, может быть использована для улучшения прогнозов относительно линейная регрессия. То, можно ли преодолеть линейную регрессию с помощью ансамблевого разброса таким образом, зависит от системы прогноза, переменной прогноза и времени выполнения заказа.

Прогнозирование размера изменений прогноза

Помимо использования для улучшения прогнозов неопределенности, ансамблевый разброс также может использоваться в качестве предиктора вероятного размера изменений среднего прогноза от одного прогноза к другому.[26] Это работает, потому что в некоторых системах ансамблевых прогнозов узкие ансамбли имеют тенденцию предшествовать небольшим изменениям среднего, в то время как широкие ансамбли имеют тенденцию предшествовать более значительным изменениям среднего. Это имеет применение в торговых отраслях, для которых может быть важно понимание вероятных размеров будущих изменений прогнозов.

Координированное исследование

Основная статья: Интерактивный большой глобальный ансамбль ТОРПЭКС

Исследование системы наблюдений и эксперимент с предсказуемостью (THORPEX) - это 10-летняя международная программа исследований и разработок, направленная на ускорение повышения точности однодневных и двухнедельных прогнозов погоды со значительными воздействиями на благо общества, экономики и окружающей среды. Он устанавливает организационную основу для решения проблем погодных исследований и прогнозов, решение которых будет ускорено за счет международного сотрудничества между академическими учреждениями, центрами оперативных прогнозов и пользователями прогностической продукции.

Одним из его ключевых компонентов является Интерактивный большой глобальный ансамбль ТОРПЭКС (TIGGE), Всемирная программа метеорологических исследований для ускорения повышения точности прогнозов погоды со значительными последствиями от 1 дня до 2 недель на благо человечества. Централизованные архивы данных прогнозов ансамблевых моделей из многих международных центров используются для обеспечения обширных обмен данными и исследования.

Смотрите также

Рекомендации

  1. ^ Кокс, Джон Д. (2002). Наблюдатели за бурей. John Wiley & Sons, Inc., стр.222–224. ISBN  978-0-471-38108-2.
  2. ^ Манусос, Питер (19 июля 2006 г.). «Системы ансамблевого прогнозирования». Центр гидрометеорологического прогнозирования. Получено 2010-12-31.
  3. ^ Вейкманн, Клаус, Джефф Уитакер, Андрес Рубичек и Кэтрин Смит (2001-12-01). Использование ансамблевых прогнозов для получения улучшенных среднесрочных (3–15 дней) прогнозов погоды. Центр климатической диагностики. Проверено 16 февраля 2007.
  4. ^ Палмер, Тим (2018). «Система ансамблевого прогнозирования ЕЦСПП: взгляд назад (более чем) на 25 лет и прогноз на 25 лет». Ежеквартальный журнал Королевского метеорологического общества. 0. arXiv:1803.06940. Bibcode:2018arXiv180306940P. Дои:10.1002 / qj.3383. ISSN  1477-870X.
  5. ^ Эпштейн, Э. (Декабрь 1969 г.). «Стохастическое динамическое предсказание». Теллус А. 21 (6): 739–759. Bibcode:1969 Расскажи ... 21..739E. Дои:10.1111 / j.2153-3490.1969.tb00483.x.
  6. ^ Лейт, К.Е. (июнь 1974 г.). «Теоретический навык прогнозов Монте-Карло». Ежемесячный обзор погоды. 102 (6): 409–418. Bibcode:1974MWRv..102..409L. Дои:10.1175 / 1520-0493 (1974) 102 <0409: TSOMCF> 2.0.CO; 2. ISSN  1520-0493.
  7. ^ Слинго, Юлия; Палмер, Тим (13 декабря 2011 г.). «Неопределенность прогноза погоды и климата». Фил. Пер. R. Soc. А. 369 (1956): 4751–4767. Bibcode:2011RSPTA.369.4751S. Дои:10.1098 / rsta.2011.0161. ISSN  1364-503X. ЧВК  3270390. PMID  22042896.
  8. ^ «Система ансамблевого прогнозирования (EPS)». ЕЦСПП. Архивировано из оригинал на 2010-10-30. Получено 2011-01-05.
  9. ^ «Количественная оценка неопределенности прогнозов | ЕЦСПП». www.ecmwf.int. 2013-11-29. Получено 2016-11-20.
  10. ^ Тот, Золтан; Калнай Евгения (Декабрь 1997 г.). «Ансамблевое прогнозирование в NCEP и метод селекции». Ежемесячный обзор погоды. 125 (12): 3297–3319. Bibcode:1997MWRv..125.3297T. CiteSeerX  10.1.1.324.3941. Дои:10.1175 / 1520-0493 (1997) 125 <3297: EFANAT> 2.0.CO; 2. ISSN  1520-0493.
  11. ^ Molteni, F .; Buizza, R .; Палмер, Т.; Петролягис, Т. (январь 1996 г.). «Система ансамблевого прогнозирования ECMWF: методология и проверка». Ежеквартальный журнал Королевского метеорологического общества. 122 (529): 73–119. Bibcode:1996QJRMS.122 ... 73M. Дои:10.1002 / qj.49712252905.
  12. ^ "Ансамбли возмущенной физики | climprediction.net". www.climateprediction.net. Получено 2016-11-20.
  13. ^ Маккейб, Энн; Суинбанк, Ричард; Теннант, Уоррен; Лок, Адриан (2016-10-01). «Представление неопределенности модели в системе прогнозирования ансамбля, допускающей конвекцию, и ее влияние на прогнозирование тумана». Ежеквартальный журнал Королевского метеорологического общества. 142 (700): 2897–2910. Bibcode:2016QJRMS.142.2897M. Дои:10.1002 / qj.2876. ISSN  1477-870X.
  14. ^ Оллинахо, Пиркка; Лок, Сара-Джейн; Лойбехер, Мартин; Бехтольд, Питер; Бельяарс, Антон; Боззо, Алессио; Forbes, Ричард М .; Хайден, Томас; Хоган, Робин Дж. (01.10.2016). «К представлению неопределенностей модели на уровне процесса: параметризации со стохастическими возмущениями в ансамбле ECMWF». Ежеквартальный журнал Королевского метеорологического общества. 143 (702): 408–422. Bibcode:2017QJRMS.143..408O. Дои:10.1002 / qj.2931. ISSN  1477-870X.
  15. ^ Christensen, H.M .; Мороз, И.М.; Палмер, Т. Н. (04.02.2015). "Стохастические и возмущенные параметрические представления неопределенности модели в параметризации конвекции". Журнал атмосферных наук. 72 (6): 2525–2544. Bibcode:2015JAtS ... 72.2525C. Дои:10.1175 / JAS-D-14-0250.1. ISSN  0022-4928.
  16. ^ Бернер, Юдифь; Ахатц, Ульрих; Батте, Лориан; Бенгтссон, Лиза; Де ла Камара, Альваро; Christensen, Hannah M .; Коланджели, Маттео; Coleman, Danielle R.B .; Кроммелин, Даан (19.07.2016). «Стохастическая параметризация: к новому взгляду на модели погоды и климата». Бюллетень Американского метеорологического общества. 98 (3): 565. arXiv:1510.08682. Bibcode:2017БАМС ... 98..565Б. Дои:10.1175 / БАМС-Д-15-00268.1. ISSN  0003-0007.
  17. ^ Buizza, R .; Milleer, M .; Палмер, Т. Н. (1999-10-01). «Стохастическое представление неопределенностей модели в системе ансамблевого прогнозирования ECMWF». Ежеквартальный журнал Королевского метеорологического общества. 125 (560): 2887–2908. Bibcode:1999QJRMS.125.2887B. Дои:10.1002 / qj.49712556006. ISSN  1477-870X.
  18. ^ Чжоу, Биньбинь и Цзюнь Ду (февраль 2010 г.). "Прогнозирование тумана на основе многомодельной системы прогнозирования мезомасштабного ансамбля" (PDF). Погода и прогнозирование. 25 (1): 303. Bibcode:2010WtFor..25..303Z. Дои:10.1175 / 2009WAF2222289.1. Получено 2011-01-02.
  19. ^ Кейн, Д. и М. Милелли (12 февраля 2010 г.). «Многомодельный метод SuperEnsemble для количественных прогнозов осадков в регионе Пьемонте». Опасные природные явления и науки о Земле. 10 (2): 265. Bibcode:2010NHESS..10..265C. Дои:10.5194 / nhess-10-265-2010.
  20. ^ Vandenbulcke, L .; и другие. (2009). «Методы супер-ансамбля: применение для прогнозирования дрейфа поверхности» (PDF). Прогресс в океанографии. 82 (3): 149–167. Bibcode:2009ПрОце..82..149В. Дои:10.1016 / j.pocean.2009.06.002.
  21. ^ а б Уорнер, Томас Томкинс (2010). Численное прогнозирование погоды и климата. Издательство Кембриджского университета. С. 266–275. ISBN  978-0-521-51389-0.
  22. ^ Palmer, T.N .; G.J. Жалюзи; Р. Хагедорн; Ф.Дж. Доблас-Рейес; Т. Юнг; М. Лойбехер (май 2005 г.). «Представление модели неопределенности в прогнозе погоды и климата». Ежегодный обзор наук о Земле и планетах. 33: 163–193. Bibcode:2005AREPS..33..163P. Дои:10.1146 / annurev.earth.33.092203.122552.
  23. ^ Leutbecher, M .; Палмер, Т. Н. (20 марта 2008 г.). «Ансамблевое прогнозирование». Журнал вычислительной физики. Прогнозирование погоды, климата и экстремальных явлений. 227 (7): 3515–3539. Bibcode:2008JCoPh.227.3515L. Дои:10.1016 / j.jcp.2007.02.014.
  24. ^ Гнейтинг, Тильманн; Балабдауи, Фадуа; Рафтери, Адриан Э. (2007-04-01). «Вероятностные прогнозы, калибровка и резкость». Журнал Королевского статистического общества, серия B. 69 (2): 243–268. CiteSeerX  10.1.1.142.9002. Дои:10.1111 / j.1467-9868.2007.00587.x.
  25. ^ Джусон, S; Брикс, А; Зиманн, С (2004). «Новая параметрическая модель для оценки и калибровки среднесрочных ансамблевых прогнозов температуры». Письма об атмосфере. 5 (5): 96–102. arXiv:физика / 0308057. Дои:10.1002 / asl.69.
  26. ^ Джусон, S; Зиманн, С (2004). «Использование ансамблевых прогнозов для прогнозирования размера изменений прогноза с применением к значению обмена погодных условий под угрозой». Письма об атмосфере. 4 (1–4): 15–27. Дои:10.1016 / S1530-261X (03) 00003-3.

дальнейшее чтение

внешняя ссылка