График Эллингема – Хортона - Ellingham–Horton graph
| Графы Эллингема – Хортона | |
|---|---|
 54-граф Эллингема – Хортона. | |
| Названный в честь | Джозеф Хортон и Марк Эллингем |
| Вершины | 54 (54-график) 78 (78-график) |
| Края | 81 (54-график) 117 (78-график) |
| Радиус | 9 (54-график) 7 (78-график) |
| Диаметр | 10 (54-график) 13 (78-график) |
| Обхват | 6 (оба) |
| Автоморфизмы | 32 (54-график) 16 (78-график) |
| Хроматическое число | 2 (оба) |
| Хроматический индекс | 3 (оба) |
| Толщина книги | 3 (оба) |
| Номер очереди | 2 (оба) |
| Характеристики | Кубический (обе) Двудольный (обе) Обычный (обе) |
| Таблица графиков и параметров | |
в математический поле теория графов, то Графы Эллингема – Хортона два 3-регулярные графики на 54 и 78 вершинах: Эллингема – Хортона, 54 графика и 78-график Эллингема – Хортона.[1] Они названы в честь Джозефа Д. Хортона и Марк Н. Эллингем, их первооткрыватели. Эти два графа служат контрпримерами к гипотезе В. Т. Тутте что каждый кубический 3-связный двудольный граф является Гамильтониан.[2] В толщина книги из Эллингема-Хортона, 54 графика и Эллингема-Хортона 78-график равно 3 и номера очереди 2.[3]
Первым контрпримером к гипотезе Тутте был Граф Хортона, опубликовано Бонди и Мёрти (1976).[4] После графа Хортона был найден ряд меньших контрпримеров к гипотезе Тутте. Среди них 92-вершинный граф по Хортон (1982),[5] 78-вершинный граф Оуэнс (1983),[6] и два графа Эллингема – Хортона.
Первый граф Эллингема – Хортона был опубликован Эллингем (1981) и имеет порядок 78.[7] В то время это был наименьший известный контрпример к гипотезе Тутте. Второй граф Эллингема – Хортона был опубликован Эллингем и Хортон (1983) и имеет порядок 54.[8] В 1989 году был открыт граф Жоржа, самый маленький из известных в настоящее время негамильтоновых трехсвязных кубических двудольных графов, содержащий 50 вершин.[9]
Галерея
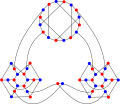
В хроматическое число 54-графа Эллингема – Хортона равно 2.

В хроматический индекс 54-графа Эллингема – Хортона равно 3.
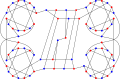
В хроматическое число 78-графа Эллингема – Хортона равно 2.

В хроматический индекс 78-графа Эллингема – Хортона равно 3.
Рекомендации
- ^ Вайсштейн, Эрик В. «Гипотеза Тутте». MathWorld.
- ^ Тутте, В. Т. (1971), "О 2-факторах бикубических графов", Дискретная математика, 1 (2): 203–208, Дои:10.1016 / 0012-365X (71) 90027-6.
- ^ Джессика Вольц, Разработка линейных макетов с помощью SAT. Магистерская работа, Тюбингенский университет, 2018 г.
- ^ Бонди, Дж. А.; Мурти, США. (1976), Теория графов с приложениями, Нью-Йорк: Северная Голландия, стр.240, ISBN 0-444-19451-7
- ^ Хортон, Дж. Д. (1982), "О двух факторах двудольных регулярных графов", Дискретная математика, 41 (1): 35–41, Дои:10.1016 / 0012-365X (82) 90079-6.
- ^ Оуэнс, П. Дж. (1983), "Двудольные кубические графы и показатель краткости", Дискретная математика, 44 (3): 327–330, Дои:10.1016 / 0012-365X (83) 90201-7.
- ^ Эллингем, М. Н. (1981), Негамильтоновы 3-связные кубически-долевые графы, Отчет об исследовании 28, Мельбурн: кафедра математики, Univ. Мельбурн.
- ^ Ellingham, M.N .; Хортон, Дж. Д. (1983), "Негамильтоновы 3-связные кубические двудольные графы", Журнал комбинаторной теории, серия B, 34 (3): 350–353, Дои:10.1016/0095-8956(83)90046-1.
- ^ Жорж, Дж. П. (1989), "Негамильтоновы бикубические графы", Журнал комбинаторной теории, серия B, 46 (1): 121–124, Дои:10.1016/0095-8956(89)90012-9.




