Цифровой биквадратный фильтр - Digital biquad filter
 | Эта статья включает в себя список общих использованная литература, но он остается в основном непроверенным, потому что ему не хватает соответствующих встроенные цитаты. (Октябрь 2015) (Узнайте, как и когда удалить этот шаблон сообщения) |
В обработка сигнала, а цифровой биквадратный фильтр это второй порядок рекурсивный линейный фильтр, содержащий два полюса и два нули. «Биквад» - это сокращение от «биквадратный", что означает, что в Z домен, его функция передачи это соотношение двух квадратичные функции:
Коэффициенты часто нормируются так, что а0 = 1:
Высокого порядка БИХ-фильтры может быть очень чувствительным к квантование их коэффициентов, и может легко стать неустойчивый. Это намного меньше проблем с фильтрами первого и второго порядка; поэтому фильтры более высокого порядка обычно реализуются как последовательно включенные биквадратные секции (и фильтр первого порядка, если необходимо). Два полюса биквадратного фильтра должны находиться внутри единичного круга, чтобы он был устойчивым. В общем, это верно для всех дискретных фильтров, т.е. все полюса должны находиться внутри единичного круга в Z-области, чтобы фильтр был устойчивым.
Реализация
Прямая форма 1
Самая простая реализация - это прямая форма 1, которая имеет следующие разностное уравнение:
![y [n] = {гидроразрыв {1} {a_ {0}}} слева (b_ {0} x [n] + b_ {1} x [n-1] + b_ {2} x [n-2] - a_ {1} y [n-1] -a_ {2} y [n-2] ight)](https://wikimedia.org/api/rest_v1/media/math/render/svg/51d2168652d5ce30472257d7d4b94d840ba67beb)
или, если нормализовано:
![y [n] = b_ {0} x [n] + b_ {1} x [n-1] + b_ {2} x [n-2] -a_ {1} y [n-1] -a_ {2 } г [п-2]](https://wikimedia.org/api/rest_v1/media/math/render/svg/dbbed7b550ce5ae4c333653731fd59815f2001fe)
Здесь , и коэффициенты определяют нули, а , определить положение полюсов.
График потока биквадратного фильтра в прямой форме 1:
Прямая форма 2
Для реализации прямой формы 1 требуется четыре регистра задержки. Эквивалентная схема - это реализация прямой формы 2, для которой требуются только два регистра задержки:
Реализация прямой формы 2 называется канонической формой, потому что она использует минимальное количество задержек, сумматоров и множителей, давая ту же передаточную функцию, что и реализация прямой формы 1. В разностные уравнения для прямой формы 2:
![y [n] = b_ {0} w [n] + b_ {1} w [n-1] + b_ {2} w [n-2],](https://wikimedia.org/api/rest_v1/media/math/render/svg/ffd7f716e1296ba7acbe9c1ffa0fe62beba53cfc)
где
![w [n] = x [n] -a_ {1} w [n-1] -a_ {2} w [n-2].](https://wikimedia.org/api/rest_v1/media/math/render/svg/6c627a74e81ff3ff1736957f11c8337bdc37ab1a)
Транспонированные прямые формы
![[икона]](http://upload.wikimedia.org/wikipedia/commons/thumb/1/1c/Wiki_letter_w_cropped.svg/20px-Wiki_letter_w_cropped.svg.png){kind=small} | Эта секция нуждается в расширении. Вы можете помочь добавляя к этому. (Октябрь 2015) |
Каждую из двух прямых форм можно транспонировать путем обращения потокового графа без изменения передаточной функции. Точки филиалов заменены на летние, а лето - на точки ветвлений.[1] Они предоставляют модифицированные реализации, которые выполняют ту же функцию передачи, которая может быть математически значимой в реальной реализации, где точность может быть потеряна при хранении состояний.
В разностные уравнения для транспонированной прямой формы 2:
![{displaystyle y [n] = b_ {0} x [n] + s_ {1} [n-1],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/781206a00e173b4bb4c8633fadc817305fb5b40f)
где
![{displaystyle s_ {1} [n] = s_ {2} [n-1] + b_ {1} x [n] -a_ {1} y [n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c3eabb9aff6fc0dd170bcb5b1cb96f79688ab09b)
и
![{displaystyle s_ {2} [n] = b_ {2} x [n] -a_ {2} y [n].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a7ce54b05bb366b4b1b07fc6d6a55fdf8ddd6e8)
Транспонированная прямая форма 1
Прямая форма 1
переносится в
Транспонированная прямая форма 2
Прямая форма 2
переносится в
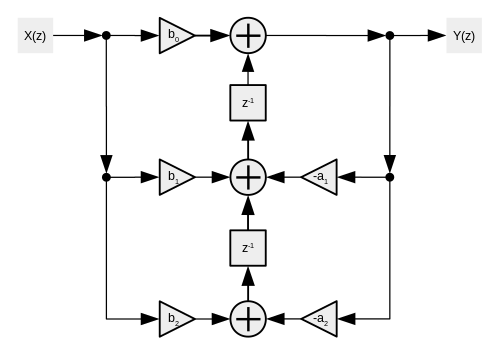
Квантованный шум
Когда выборка из n битов умножается на коэффициент из m битов, произведение имеет n + m битов. Эти продукты обычно накапливаются в регистре DSP, для добавления пяти продуктов может потребоваться 3 бита переполнения; этот регистр часто бывает достаточно большим, чтобы содержать n + m + 3 бита. Z−1 реализуется путем сохранения значения для одного времени выборки; в этом регистре хранения обычно n битов, регистр накопителя округляется до n битов, и это вносит шум квантования.
В конфигурации прямой формы 1 имеется единственная функция квантования / округления.
.
В компоновке прямой формы 2 есть функция квантования / округления для промежуточного значения. В каскаде значение может не нуждаться в округлении между этапами, но окончательный результат может нуждаться в округлении.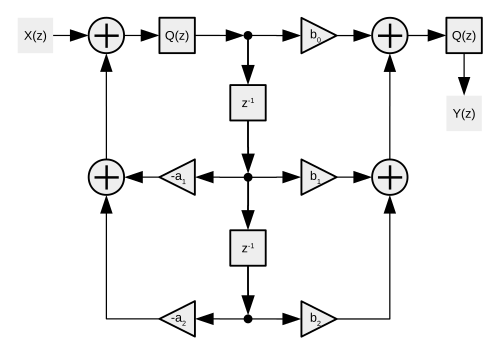
.
DSP с фиксированной точкой обычно предпочитает непереносимые формы и имеет аккумулятор с большим количеством битов и округляется при хранении в основной памяти. DSP с плавающей запятой обычно предпочитает транспонированную форму, каждое умножение и потенциально каждое сложение округляются; сложения являются результатом более высокой точности, когда оба операнда имеют одинаковую величину.