Кубооктаэдрическая призма - Cuboctahedral prism
| Кубооктаэдрическая призма | |
|---|---|
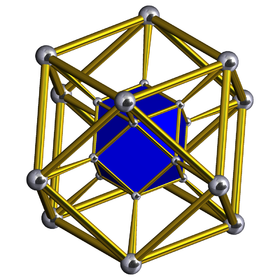 Диаграмма Шлегеля Показана одна кубооктаэдрическая ячейка | |
| Тип | Призматический однородный 4-многогранник |
| Единый индекс | 50 |
| Символ Шлефли | т1,3{3,4,2} или r {3,4} × {} т0,2,3{3,3,2} или rr {3,3} × {} |
| Кокстер-Дынкин | |
| Клетки | 2 (3.4.3.4 ) 8 (3.4.4 ) 6 (4.4.4 ) |
| Лица | 16 {3} 12+24 {4} |
| Края | 60 |
| Вершины | 24 |
| Фигура вершины | 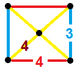 Прямоугольный пирамида |
| Группа симметрии | [3,4,2], порядок 96 [3,3,2], порядок 48 |
| Характеристики | выпуклый |
В геометрия, а кубооктаэдрическая призма выпуклый равномерный 4-многогранник. В этом 4-многограннике 16 многогранник ячеек: 2 кубооктаэдр соединены 8 треугольные призмы, и 6 кубики.
Это одна из 18 однородных многогранных призм, созданных с помощью призмы для соединения пар параллельно Платоновы тела и Архимедовы тела.
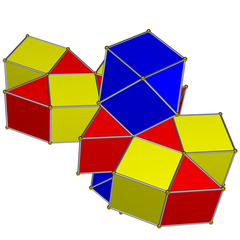 Сеть |  Прозрачный Диаграмма Шлегеля |
Альтернативные названия
- Кубооктаэдрическая диадическая призма Норман В. Джонсон
- Справиться (Джонатан Бауэрс: для кубооктаэдрической призмы)
- Ромбиоктаэдрическая призма
- Ромбиоктаэдрическая гиперпризма
внешняя ссылка
- 6. Выпуклая однородная призматическая полихора - Модель 50., Георгий Ольшевский.
- Клитцинг, Ричард. "4D равномерные многогранники (полихоры) x o3x4o - справиться".
| Этот 4-многогранник статья - это заглушка. Вы можете помочь Википедии расширяя это. |
