Треск - Crackling noise

Не путать с Треск.
Случайный шум, создаваемый горящими углями, является примером треска.

Треск возникает, когда система подвергается воздействию внешней силы, и она реагирует через события, которые кажутся очень похожи во многих разных масштабах. В классической системе обычно два состояния: включено и выключено. Однако иногда может существовать промежуточное состояние. Этот шум можно разделить на три основные категории: первая - выскакивают где события очень похожей величины происходят непрерывно и случайным образом, например Попкорн; второй щелчок когда в системе мало изменений до тех пор, пока не будет превышен критический порог, после чего вся система переходит из одного состояния в другое, например щелкать карандашом; третий треск который представляет собой комбинацию щелчка и привязки, где есть несколько небольших и несколько крупных событий с законом отношения, предсказывающим их возникновение, называемое универсальность.[1] Потрескивание можно наблюдать во многих природных явлениях, например. мятую бумагу,[2] пожары, землетрясения и намагничивание магнитов.

Некоторые из этих систем обратимы, например, размагничивание (путем нагревания магнита до Температура Кюри ),[3] в то время как другие являются необратимыми, например, лавина (когда снег может двигаться только с горы), но многие системы имеют положительное смещение, заставляющее в конечном итоге переходить из одного состояния в другое, например, гравитация или другая внешняя сила.

Теория

Шум Баркгаузена

Кривая намагничивания (J) или плотности потока (B) как функция напряженности магнитного поля (H) в ферромагнитном материале. На вставке прыжки Баркгаузена.

Исследования по изучению малых возмущений в больших областях начались в конце 1910-х годов, когда Генрих Баркгаузен исследовали, как домены или диполи внутри ферромагнитный материал изменился под действием внешнего магнитного поля. При размагничивании диполи магнита указывают в случайных направлениях, поэтому чистая магнитная сила от всех диполей будет равна нулю. Путем наматывания железного стержня на проволоку и пропускания электрического тока через провод создается магнитное поле, перпендикулярное катушке (Правило правой руки Флеминга для катушки), это заставляет диполи внутри магнита выравниваться по внешнему полю.

Вопреки тому, что в то время считалось, что эти домены непрерывно меняются один за другим, Баркгаузен обнаружил, что кластеры доменов меняются небольшими дискретными шагами.[4] Путем наматывания вторичной катушки вокруг шины, подключенной к динамику или детектору, когда кластер доменов меняет ориентацию, происходит изменение магнитного потока, это нарушает ток во вторичной катушке и, следовательно, вызывает выходной сигнал. При воспроизведении вслух это называется Шум Баркгаузена, намагниченность магнита дискретно возрастает в зависимости от плотности потока.[5]

Закон Гутенберга – Рихтера

Дальнейшее исследование потрескивающего шума было проведено в конце 1940-х гг. Чарльз Фрэнсис Рихтер и Бено Гутенберг который исследовал землетрясения аналитически. До изобретения известного шкала Рихтера, то Шкала интенсивности Меркалли было использовано; это субъективное измерение того, насколько землетрясение нанесло ущерб собственности, т.е. II будут небольшие колебания и движущиеся объекты, а XII - широко распространенное разрушение всех зданий. Шкала Рихтера - это логарифмическая шкала, которая измеряет энергию и амплитуду вибраций, рассеиваемых от эпицентра землетрясения, т.е. землетрясение силой 7,0 баллов в 10 раз сильнее землетрясения 6,0 балла. Вместе с Гутенбергом они открыли Закон Гутенберга – Рихтера которое является соотношением распределения вероятностей между силой землетрясения и вероятностью его возникновения. В нем говорится, что небольшие землетрясения случаются гораздо чаще, а более крупные землетрясения - очень редко.[6]

Закон Гутенберга – Рихтера[7] показывает обратную зависимость мощности между количеством происходящих землетрясений N и его величина M с константой пропорциональности б и перехватитьа.

Моделирование

Эволюция двухмерного моделирования клеточного автомата с течением времени. Сначала система выскакивает, затем она трескается, некоторые маленькие и некоторые большие кластеры становятся белыми и остаются белыми, наконец, система переходит в глобальное положительное состояние (+1).

Чтобы по-настоящему смоделировать такую ​​среду, потребуется непрерывная бесконечная трехмерная система, однако из-за вычислительных ограничений двумерная клеточные автоматы может использоваться для получения близкого приближения; миллиона ячеек в виде матрицы размером 1000x1000 достаточно для тестирования большинства сценариев. Каждая ячейка хранит две части информации; сила, приложенная к ячейке, которая является непрерывной величиной, и состояние ячейки, которое является целочисленным значением либо +1 (включен), либо -1 (выключен).

Параметризация

Чистая сила состоит из трех компонентов, которые могут соответствовать физическим характеристикам любой системы шума потрескивания; первое - внешнее силовое поле (K), которое увеличивается со временем (t). Вторая составляющая - это сила, которая зависит от суммы состояний соседних ячеек (S), а третья - случайная составляющая (r), масштабируемая по (X).[8]

Внешняя сила K умножается на время (т), где K является положительной скалярной константой, но может быть как переменной, так и отрицательной. S представляет состояние ячейки (+1 или -1), второй компонент берет сумму четырех соседних состояний ячейки (вверх, вниз, влево и вправо) и умножает ее на другую скалярную величину, это аналогично константе связи (J). Генератор случайных чисел (р) - это нормально распределенный диапазон значений со средним нулевым и фиксированным стандартным отклонением (рσ), это также умножается на скалярную константу (Икс). Из трех составляющих чистой силы (F), соседние и случайные компоненты могут давать положительные и отрицательные значения, в то время как внешняя сила является только положительной, что означает, что к системе применяется прямое смещение, которое со временем становится доминирующей силой.

Если результирующая сила на ячейке положительна, она включит (+1) и выключит (-1), если сила на ячейку отрицательная. В 2D-системе существует множество возможных комбинаций и расположений состояний, но их можно сгруппировать в три области: два глобальных стабильных состояния со всеми +1 или всеми -1 и нестабильное состояние между ними, где есть смесь обоих. состояния. Традиционно, если система нестабильна, она вскоре перейдет в одно из глобальных состояний, однако при идеальных условиях, то есть в критической точке, между двумя глобальными состояниями может образоваться метастабильное состояние, которое является устойчивым только в том случае, если параметры суммарной силы сбалансированы. Граничные условия для матрицы повторяются сверху вниз и слева направо, проблемы для угловых ячеек могут быть устранены с помощью большой матрицы.

Щелчок, треск и треск

Можно сформировать три утверждения, чтобы описать, когда и как система реагирует на стимул. Разница между внешним полем и другими компонентами определяет, лопнет ли система или потрескивает, но есть также особый случай: если модуль случайной и соседней составляющих намного больше, чем внешнее поле, система переходит в нулевую плотность. а затем замедляет скорость конверсии.

Поппинг - это когда в системе есть небольшие возмущения, которые обратимы и оказывают незначительное влияние на глобальное состояние системы.

Привязка - это когда большие кластеры ячеек или вся система переходит в другое состояние, то есть все +1 или все -1. Вся система перевернется только тогда, когда она достигнет критического или переломный момент.

Растрескивание наблюдается, когда система испытывает треск обратимых малых и больших кластеров. Система постоянно разбалансирована и пытается достичь равновесия, которое невозможно из-за внутренних или внешних сил.

Физический смысл компонентов

Случайная составляющая (р)

Моделируя землетрясения, можно соблюдать закон Гутенберга-Рихтера, в этой системе случайная составляющая представляла бы случайные возмущения на земле и в воздухе, и это может быть что угодно: от сильной погодной системы, естественных непрерывных стимулов, таких как течение реки, волн попадание на береговую линию или деятельность человека, например, бурение. Это очень похоже на эффект бабочки где невозможно предсказать будущий исход события или проследить до исходного состояния с установленного времени во время моделирования, и на макроскопическом уровне это кажется незначительным, но на микроскопическом уровне могло быть причиной цепной реакции событий; включение одной ячейки может отвечать за включение всей системы.

Соседний компонент (ΣS)

Соседний компонент для физических объектов, таких как скалы или тектонические плиты, - это просто описание законов движения Ньютона, если плита движется и сталкивается с другой плитой, другая плита будет обеспечивать силу реакции, аналогично, если большая коллекция рыхлых частиц (валуны, разломы) прижимается к своему соседу, соседняя частица / объект также будет двигаться.

Внешняя сила (K)

Внешняя сила - это длительные движения тектонических плит или течения жидких горных пород в пределах верхняя мантия, который представляет собой непрерывную силу, приложенную, в конечном итоге, пластина отскочит назад или сломается, снимая напряжение с системы, чтобы перевернуть ее в стабильное состояние, то есть землетрясение. Вулканы похожи тем, что нарастание давления магмы под ними в конечном итоге преодолеет слой сухой породы наверху, вызывая извержение. Такие модели можно использовать для прогнозирования возникновения землетрясений и извержений вулканов в активных регионах и прогнозирования афтершоков, которые являются обычным явлением после крупных событий.

Практическое применение

Во время намагничивания магнита; внешнее поле - это приложенное электрическое поле, соседняя составляющая - это эффект локализованных магнитных полей диполей, а случайная составляющая представляет другие возмущения от внешних или внутренних стимулов. У этого есть много практических применений, производитель может использовать этот тип моделирования для неразрушающего тестирования своих магнитов, чтобы увидеть, как они реагируют в определенных условиях. Чтобы проверить его намагниченность после принятия большой силы, например, удара молотком или падения его на пол, можно было внезапно увеличить внешнюю силу (ЧАС) или константа связи (J). Для проверки тепловых условий можно применить граничное условие к одному краю с увеличением тепловых флуктуаций (увеличение Икс), для этого потребуется трехмерная модель.

Мир бизнеса

Поведение цен на акции продемонстрировало свойства универсальности. Взяв исторические данные о ценах на акции компании,[9] расчет ежедневного возвращается а затем нанесение этого на гистограмму даст гауссовское распределение. Цены на акции будут постоянно колебаться с небольшими колебаниями, а с большими - гораздо реже; фондовую биржу можно интерпретировать как силу, ответственную за приведение цены акций к равновесию путем корректировки цены на спрос и предложение квота.

Слияния компаний, при которых регулярно образуются небольшие компании, часто стартапы, которые очень нестабильны, если они выживут в течение определенного периода времени, они, вероятно, продолжат расти, когда они станут достаточно большими, они смогут покупать другие более мелкие компании. собственный размер. Это очень похоже на то, как крупные компании покупают своих конкурентов, чтобы увеличить свою долю на рынке, и так далее, и так далее, пока рынок не станет насыщенным.

Примеры в мире природы

Системы в реальном мире не могут оставаться в постоянном равновесии, поскольку существует слишком много внешних факторов, влияющих на состояние системы. Система может либо находиться во временном равновесии, а затем внезапно выйти из строя из-за стимула, либо находиться в постоянном состоянии смены фаз из-за внешней силы, пытающейся сбалансировать систему. Эти системы наблюдают треск, щелчки и треск.[10]

  • Смятая бумага вызывает треск

  • Частота землетрясений в зависимости от магнитуды землетрясения

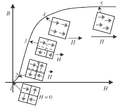
  • Скорость, с которой домен магнита выравнивается по внешнему магнитному полю.

  • Случайное время появления кукурузы

  • Случай срабатывания лавины из-за накопления избыточного снега

  • Щелчок карандаша из-за неупругих механических свойств древесины.

  • Точный момент срабатывания оползня из-за неустойчивых камней и валунов

  • Вулкан в конечном итоге извергнется, когда давление внутреннего потока магмы превысит герметичность.

  • Подводная лодка использует гидросамолеты для постоянной регулировки глубины, так как она не может оставаться в равновесии (плавучесть = вес) без внешней силы.

  • Силы Ван-дер-Ваальса означают, что жировые шарики, образующиеся на поверхности воды, будут притягиваться друг к другу, чтобы уменьшить свободную энергию и стать более крупными кластерами.

  • Рис Криспис потрескивает при добавлении молока

использованная литература

  1. ^ «В загадочном образце сходятся математика и природа | Quanta Magazine». www.quantamagazine.org. Получено 2016-11-27.
  2. ^ Houle, Paul A .; Сетна, Джеймс П. (1996-07-01). «Акустическая эмиссия от мятой бумаги». Физический обзор E. Американское физическое общество (APS). 54 (1): 278–283. arXiv:cond-mat / 9512055v1. Дои:10.1103 / Physreve.54.278. ISSN  1063-651X.
  3. ^ «Точка Кюри | физика». Британская энциклопедия. Получено 2016-11-27.
  4. ^ Шредер, Мальте (2013). Треск при фракционной перколяции - случайно распределенные прерывистые скачки при взрывной перколяции. Институт динамики и самоорганизации Макса Планка.
  5. ^ «Доменная теория ферромагнетизма». www.gitam.edu. Кафедра инженерной физики. Архивировано из оригинал на 2016-11-20. Получено 2016-11-27.
  6. ^ «Информация о землетрясениях для мира». Геологическая служба США, Национальный центр информации о землетрясениях. Архивировано из оригинал на 2008-03-28.
  7. ^ Гутенберг, Б. (1954). Сейсмичность Земли и связанные с ней явления. Принстон: Издательство Принстонского университета.
  8. ^ Сетна, Джеймс. Треск. Лаборатория атомной физики и физики твердого тела, Кларк Холл, Корнельский университет, Итака, США: Macmillan Magazines Ltd.
  9. ^ "Yahoo Finance UK". Yahoo Finance UK. Получено 2016-11-27.
  10. ^ Али, Махфудж (2015). Потрескивающий шум. Гилфорд, Великобритания: Университет Суррея, факультет физики.