Проблема со сборщиками купонов - Coupon collectors problem

График количества купонов, п против ожидаемого количества испытаний (то есть времени), необходимого для их сбора, E (Т )

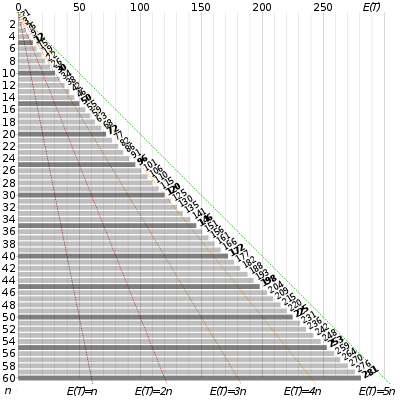
В теория вероятности, то проблема сборщика купонов описывает конкурсы «собери все купоны и выиграй». Он задает следующий вопрос: если в каждой коробке марки зерновых есть купон, и есть ли п различных типов купонов, какова вероятность того, что более т ящики нужно покупать, чтобы собрать все п купоны? Альтернативное утверждение: Дано п купонов, сколько купонов, по вашему мнению, вам нужно будет нарисовать с заменой, прежде чем использовать каждый купон хотя бы один раз? Математический анализ проблемы показывает, что ожидаемое число необходимых испытаний растет по мере ${\displaystyle \Theta (n\log(n))}$.^[а] Например, когда п = 50 требуется около 225^[b] в среднем для сбора всех 50 купонов.

Решение

Расчет ожидания

Позволять Т пора собрать все п купоны, и пусть т_я пора собирать я-й купон после я - Собрано 1 купон. потом ${\displaystyle T=t_{1}+\cdots +t_{n}}$. Думать о Т и т_я в качестве случайные переменные. Обратите внимание, что вероятность собрать новый купон ${\displaystyle p_{i}={\frac {n-(i-1)}{n}}={\frac {n-i+1}{n}}}$. Следовательно, ${\displaystyle t_{i}}$ имеет геометрическое распределение с ожиданием ${\displaystyle {\frac {1}{p_{i}}}={\frac {n}{n-i+1}}}$. Посредством линейность ожиданий у нас есть:

${\displaystyle {\begin{aligned}\operatorname {E} (T)&{}=\operatorname {E} (t_{1}+t_{2}+\cdots +t_{n})\\&{}=\operatorname {E} (t_{1})+\operatorname {E} (t_{2})+\cdots +\operatorname {E} (t_{n})\\&{}={\frac {1}{p_{1}}}+{\frac {1}{p_{2}}}+\cdots +{\frac {1}{p_{n}}}\\&{}={\frac {n}{n}}+{\frac {n}{n-1}}+\cdots +{\frac {n}{1}}\\&{}=n\cdot \left({\frac {1}{1}}+{\frac {1}{2}}+\cdots +{\frac {1}{n}}\right)\\&{}=n\cdot H_{n}.\end{aligned}}}$

Здесь ЧАС_п это п-го номер гармоники. С использованием асимптотика гармонических чисел, получаем:

${\displaystyle \operatorname {E} (T)=n\cdot H_{n}=n\log n+\gamma n+{\frac {1}{2}}+O(1/n),}$

куда ${\displaystyle \gamma \approx 0.5772156649}$ это Константа Эйлера – Маскерони.

Теперь можно использовать Неравенство Маркова чтобы ограничить желаемую вероятность:

${\displaystyle \operatorname {P} (T\geq cnH_{n})\leq {\frac {1}{c}}.}$

Расчет дисперсии

Использование независимости случайных величин т_я, мы получаем:

${\displaystyle {\begin{aligned}\operatorname {Var} (T)&{}=\operatorname {Var} (t_{1}+\cdots +t_{n})\\&{}=\operatorname {Var} (t_{1})+\operatorname {Var} (t_{2})+\cdots +\operatorname {Var} (t_{n})\\&{}={\frac {1-p_{1}}{p_{1}^{2}}}+{\frac {1-p_{2}}{p_{2}^{2}}}+\cdots +{\frac {1-p_{n}}{p_{n}^{2}}}\\&{}<\left({\frac {n^{2}}{n^{2}}}+{\frac {n^{2}}{(n-1)^{2}}}+\cdots +{\frac {n^{2}}{1^{2}}}\right)\\&{}=n^{2}\cdot \left({\frac {1}{1^{2}}}+{\frac {1}{2^{2}}}+\cdots +{\frac {1}{n^{2}}}\right)\\&{}<{\frac {\pi ^{2}}{6}}n^{2}\end{aligned}}}$

поскольку ${\displaystyle {\frac {\pi ^{2}}{6}}={\frac {1}{1^{2}}}+{\frac {1}{2^{2}}}+\cdots +{\frac {1}{n^{2}}}+\cdots }$ (видеть Базельская проблема ).

Теперь можно использовать Неравенство Чебышева чтобы ограничить желаемую вероятность:

${\displaystyle \operatorname {P} \left(|T-nH_{n}|\geq cn\right)\leq {\frac {\pi ^{2}}{6c^{2}}}.}$

Оценки хвоста

Другая верхняя граница может быть получена из следующего наблюдения. Позволять ${\displaystyle {Z}_{i}^{r}}$ обозначают событие, которое ${\displaystyle i}$-й купон не был выбран в первом ${\displaystyle r}$ испытания. Потом:

${\displaystyle {\begin{aligned}P\left[{Z}_{i}^{r}\right]\leq \left(1-{\frac {1}{n}}\right)^{r}\leq e^{-r/n}\end{aligned}}}$

Таким образом, для ${\displaystyle r=\beta n\log n}$, у нас есть ${\displaystyle P\left[{Z}_{i}^{r}\right]\leq e^{(-\beta n\log n)/n}=n^{-\beta }}$.

${\displaystyle {\begin{aligned}P\left[T>\beta n\log n\right]=P\left[\bigcup _{i}{Z}_{i}^{\beta n\log n}\right]\leq n\cdot P[{Z}_{1}^{\beta n\log n}]\leq n^{-\beta +1}\end{aligned}}}$

Расширения и обобщения

• Пьер-Симон Лаплас, но также Пол Эрдёш и Альфред Реньи, доказал предельную теорему для распределения Т. Этот результат является дальнейшим расширением предыдущих оценок.

${\displaystyle \operatorname {P} (T<n\log n+cn)\to e^{-e^{-c}},{\text{ as }}n\to \infty .}$

• Дональд Дж. Ньюман и Лоуренс Шепп дал обобщение проблемы сборщика купонов, когда м необходимо собрать копии каждого купона. Позволять Т_м быть в первый раз м собираются копии каждого купона. Они показали, что ожидание в этом случае удовлетворяет:

${\displaystyle \operatorname {E} (T_{m})=n\log n+(m-1)n\log \log n+O(n),{\text{ as }}n\to \infty .}$

Здесь м фиксированный. Когда м = 1 мы получаем предыдущую формулу математического ожидания.

• Общее обобщение, также принадлежащее Эрдешу и Реньи:

${\displaystyle \operatorname {P} \left(T_{m}<n\log n+(m-1)n\log \log n+cn\right)\to e^{-e^{-c}/(m-1)!},{\text{ as }}n\to \infty .}$

• В общем случае неравномерного распределения вероятностей согласно Филипп Флажоле,^[1]

${\displaystyle \operatorname {E} (T)=\int _{0}^{\infty }\left(1-\prod _{i=1}^{n}\left(1-e^{-p_{i}t}\right)\right)dt.}$

Смотрите также

• Оценка Уоттерсона
• Проблема дня рождения

Примечания

1. Здесь и в этой статье «журнал» относится к натуральный логарифм а не логарифм с другим основанием. Использование Θ здесь вызывает нотация большой O.
2. E (50) = 50 (1 + 1/2 + 1/3 + ... + 1/50) = 224,9603, ожидаемое количество попыток собрать все 50 купонов. Приближение ${\displaystyle n\log n+\gamma n+1/2}$ для этого ожидаемого числа дает в этом случае ${\displaystyle 50\log 50+50\gamma +1/2\approx 195.6011+28.8608+0.5\approx 224.9619}$.

Рекомендации

1. Флажолет, Филипп; Гарди, Даниэль; Thimonier, Loÿs (1992), «Парадокс дня рождения, сборщики купонов, алгоритмы кэширования и самоорганизующийся поиск», Дискретная прикладная математика, 39 (3): 207–229, CiteSeerX  10.1.1.217.5965, Дои:10.1016 / 0166-218x (92) 90177-c

• Блом, Гуннар; Холст, Ларс; Санделл, Деннис (1994), "7,5 сборов купонов I, 7,6 сборов купонов II и 15,4 купонов III", Проблемы и снимки из мира вероятностей, Нью-Йорк: Springer-Verlag, стр. 85–87, 191, ISBN  0-387-94161-4, МИСТЕР  1265713.
• Докинз, Брайан (1991), "Проблема Шивон: новый взгляд на сборщика купонов", Американский статистик, 45 (1): 76–82, Дои:10.2307/2685247, JSTOR  2685247.
• Эрдеш, Пол; Реньи, Альфред (1961), «О классической проблеме теории вероятностей» (PDF), Magyar Tudományos Akadémia Matematikai Kutató Intézetének Közleményei, 6: 215–220, МИСТЕР  0150807.
• Лаплас, Пьер-Симон (1812), Аналитическая теория вероятностей, стр. 194–195.
• Ньюман, Дональд Дж.; Шепп, Лоуренс (1960), "Проблема двойного кубка Дикси", Американский математический ежемесячный журнал, 67 (1): 58–61, Дои:10.2307/2308930, JSTOR  2308930, МИСТЕР  0120672
• Флажоле, Филипп; Гарди, Даниэль; Тимонье, Лос (1992), «Парадокс дней рождений, сборщики купонов, алгоритмы кеширования и самоорганизующийся поиск», Дискретная прикладная математика, 39 (3): 207–229, Дои:10.1016 / 0166-218X (92) 90177-C, МИСТЕР  1189469.
• Исаак, Ричард (1995), «8.4 Проблема коллекционера купонов решена», Удовольствия от вероятности, Тексты для бакалавриата по математике, Нью-Йорк: Springer-Verlag, стр. 80–82, ISBN  0-387-94415-X, МИСТЕР  1329545.
• Мотвани, Раджив; Рагхаван, Прабхакар (1995), «3.6. Проблема коллекционера купонов», Рандомизированные алгоритмы, Кембридж: Издательство Кембриджского университета, стр. 57–63, ISBN  9780521474658, МИСТЕР  1344451.

внешняя ссылка

• "Проблема со сборщиком купонов " к Эд Пегг младший, то Вольфрам Демонстрационный проект. Пакет Mathematica.
• Сколько одиночных, двойных, тройных и т. Д. Следует ожидать сборщику купонов?, короткое примечание Дорон Зейлбергер.