Угловая передаточная матрица - Corner transfer matrix

В статистическая механика, то матрица переноса угла описывает эффект добавления квадранта к решетке. Представлен Родни Бакстер в 1968 году как расширение матрицы переноса строк Крамерса-Ваннье, он обеспечивает мощный метод изучения решетчатые модели. Расчеты с использованием угловых передаточных матриц привели Бакстера к точному решению модель жесткого шестиугольника в 1980 г.

Определение

Рассмотрим модель IRF (взаимодействие-круглое лицо), т.е. модель квадратной решетки с вращение σ_я назначен каждому сайту я и взаимодействия, ограниченные вращениями вокруг общего лица. Пусть полная энергия определяется выражением

${displaystyle E=sum _{all atop faces}epsilon left(sigma _{i},sigma _{j},sigma _{k},sigma _{l}ight),}$

где для каждого лица окружающие участки я, j, k и л расположены следующим образом:

Для решетки с N сайты, функция распределения является

${displaystyle Z_{N}=sum _{all atop spins}prod _{all atop faces}wleft(sigma _{i},sigma _{j},sigma _{k},sigma _{l}ight),}$

где сумма берется по всем возможным конфигурациям спинов и ш - вес Больцмана

${displaystyle wleft(sigma _{i},sigma _{j},sigma _{k},sigma _{l}ight)=exp left(-epsilon left(sigma _{i},sigma _{j},sigma _{k},sigma _{l}ight)/k_{B}Tight).}$

Для упрощения обозначений мы используем ферромагнитная решетка типа Изинга где каждый спин имеет значение +1 или -1, а основное состояние задается всеми спинами вверх (т.е. полная энергия минимизируется, когда все спины на решетке имеют значение +1). Мы также предполагаем, что решетка имеет 4-кратную вращательную симметрию (с точностью до граничных условий) и инвариантна к отражению. Эти упрощающие предположения не имеют решающего значения, и распространить определение на общий случай относительно просто.

Теперь рассмотрим квадрант решетки, показанный ниже:

Внешним граничным узлам, отмеченным треугольниками, присваиваются их спины основного состояния (+1 в данном случае). Участки, отмеченные светлыми кружками, образуют внутренние границы квадранта; связанные с ними спиновые множества помечены {σ₁, ..., σ_м} и {σ '₁, ..., σ '_м}, где σ₁ = σ '₁. Есть 2^м возможных конфигураций для каждой внутренней границы, поэтому мы определяем 2^м×2^м матрица по элементам

${displaystyle A_{sigma |sigma '}=delta left(sigma _{1},sigma _{1}'ight)sum _{interior atop spins}prod _{all atop faces}wleft(sigma _{i},sigma _{j},sigma _{k},sigma _{l}ight).}$

Матрица А, тогда - матрица переноса угла для данного квадранта решетки. Поскольку внешние граничные спины фиксированы и сумма рассчитывается по всем внутренним спинам, каждая запись А является функцией спинов внутренней границы. Дельта Кронекера в выражении гарантирует, что σ₁ = σ '₁, поэтому, заказав конфигурации соответствующим образом, мы можем отлить А в виде блочно-диагональной матрицы:

${displaystyle {egin{array}{cccc}&&{egin{array}{ccccc}sigma _{1}'=+1&&&&sigma _{1}'=-1end{array}}A&=&left[{egin{array}{ccccccc}&&&|&A_{+}&&|&&0&&&|-&-&-&|&-&-&-&&&|&0&&|&&A_{-}&&&|end{array}}ight]&{egin{array}{c}sigma _{1}=+1\\sigma _{1}=-1end{array}}end{array}}}$

Матрицы углового переноса связаны со статистической суммой просто. В нашем упрощенном примере мы строим полную решетку из четырех повернутых копий квадранта решетки, где внутренние граничные спиновые множества σ, σ ', σ "и σ'" могут различаться:

Статистическая сумма затем записывается в терминах матрицы передачи угла А в качестве

${displaystyle Z_{N}=sum _{sigma ,sigma ',sigma '',sigma '''}A_{sigma |sigma '}A_{sigma '|sigma ''}A_{sigma ''|sigma '''}A_{sigma '''|sigma }={ extrm {tr}}A^{4}.}$

Обсуждение

Отношение рекурсии

Матрица углового переноса А_2^м (определено для м×м квадрант) может быть выражен через меньшие угловые передаточные матрицы А_2^м-1 и А_2^м-2 (определено для уменьшенного (м-1)×(м-1) и (м-2)×(м-2) квадранты соответственно). Это рекурсивное соотношение позволяет, в принципе, итеративное вычисление матрицы переноса угла для любого квадранта решетки конечного размера.

Как и их аналоги из строки в строку, матрицы переноса углов могут быть разложены на матрицы переноса граней, которые соответствуют добавлению одной грани к решетке. Для приведенного ранее квадранта решетки матрицы переноса лиц имеют размер 2^м×2^м и определяется по входам

${displaystyle left(U_{i}ight)_{sigma |sigma '}=delta left(sigma _{1},sigma _{1}'ight)cdots delta left(sigma _{i-1},sigma _{i-1}'ight)wleft(sigma _{i},sigma _{i+1},sigma _{i}',sigma _{i-1}ight)delta left(sigma _{i+1},sigma _{i+1}'ight)cdots delta left(sigma _{m},sigma _{m}'ight),}$

где 2 ≤ я ≤ м+1. В частности, около внешней границы

${displaystyle left(U_{m}ight)_{sigma |sigma '}=delta left(sigma _{1},sigma _{1}'ight)cdots delta left(sigma _{m-1},sigma _{m-1}'ight)wleft(sigma _{m},+1,sigma _{m}',sigma _{m-1}ight),}$

${displaystyle left(U_{m+1}ight)_{sigma |sigma '}=delta left(sigma _{1},sigma _{1}'ight)cdots delta left(sigma _{m},sigma _{m}'ight)wleft(+1,+1,+1,sigma _{m}ight).}$

Итак, угловая матрица переноса А факторизуется как

${displaystyle A=F_{2}cdots F_{m+1},}$

куда

${displaystyle F_{j}=U_{m+1}cdots U_{j}.}$

Графически это соответствует:

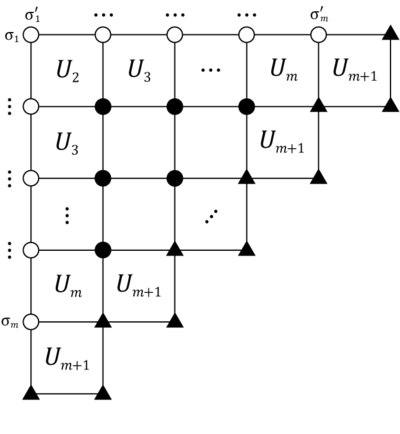
Нам также потребуется 2^м×2^м матрицы А* и А**, определено для каждой записи

${displaystyle left(A^{*}ight)_{sigma |sigma '}=delta left(sigma _{1},sigma _{1}'ight)A_{sigma _{2},ldots ,sigma _{m}|sigma _{2}',ldots ,sigma _{m}'},}$

${displaystyle left(A^{**}ight)_{sigma |sigma '}=delta left(sigma _{1},sigma _{1}'ight)delta left(sigma _{2},sigma _{2}'ight)A_{sigma _{3},ldots ,sigma _{m}|sigma _{3}',ldots ,sigma _{m}'},}$

где А матрицы, элементы которых появляются на правой стороне, имеют размер 2^м-1×2^м-1 и 2^м-2×2^м-2 соответственно. Это более четко записано как

${displaystyle A^{*}=I_{2}otimes A_{2^{m-1}}=left[{egin{array}{cc}A&0�&Aend{array}}ight],}$

${displaystyle A^{**}=I_{2}otimes I_{2}otimes A_{2^{m-2}}=left[{egin{array}{cccc}A&0&0&0�&A&0&0�&0&A&0�&0&0&Aend{array}}ight].}$

Теперь из определений А, А*, А**, U_я и F_j, у нас есть

${displaystyle A^{*}=F_{3}cdots F_{m+1},A^{**}=F_{4}cdots F_{m+1}}$

${displaystyle Rightarrow A=F_{2}A^{*},A^{*}=F_{3}A^{**}}$

${displaystyle Rightarrow A=A^{*}left(A^{**}ight)^{-1}U_{2}A^{*},}$

что дает рекурсивное соотношение для А_2^м с точки зрения А_2^м-1 и А_2^м-2.

Диагональная форма

При использовании угловых передаточных матриц для выполнения расчетов, как аналитически, так и численно удобно работать с их диагональными формами. Для облегчения этого рекурсивное отношение можно переписать непосредственно в терминах диагональные формы и матрицы собственных векторов из А, А* и А**.

Напомним, что решетка в нашем примере инвариантна к отражению в том смысле, что

${displaystyle wleft(sigma _{i},sigma _{j},sigma _{k},sigma _{l}ight)=wleft(sigma _{k},sigma _{j},sigma _{i},sigma _{l}ight)=wleft(sigma _{i},sigma _{l},sigma _{k},sigma _{j}ight),}$

Мы видим, что А является симметричной матрицей (т.е. диагонализируется ортогональная матрица ). Итак, мы пишем

${displaystyle A=alpha _{m}PA_{d}P^{T},}$

куда А_d - диагональная матрица (нормализованная так, что ее наибольший числовой элемент равен 1), α_м - наибольшее собственное значение А, и п^Тп = я. Аналогично для А* и А**, у нас есть

${displaystyle A^{*}=alpha _{m-1}P^{*}A_{d}^{*}left(P^{*}ight)^{T},}$

${displaystyle A^{**}=alpha _{m-2}P^{**}A_{d}^{**}left(P^{**}ight)^{T},}$

куда А_d*, А_d**, п* и п** определены аналогично А* и А**, то есть через меньшие (нормированные) диагональные формы и (ортогональные) матрицы собственных векторов А_2^м-1 и А_2^м-2.

Подставляя эти диагонализации в рекурсивное соотношение, получаем

${displaystyle A_{t}=kappa RA_{d}R^{T},}$

куда

${displaystyle kappa ={frac {alpha _{m}alpha _{m-2}}{alpha _{m-1}^{2}}},}$

${displaystyle R=left(P^{*}ight)^{T}P,}$

${displaystyle A_{t}=A_{d}^{*}left(R^{*}ight)^{T}left(A_{d}^{**}ight)^{-1}U_{2}R^{*}A_{d}^{*}.}$

Сейчас же А_т также симметричен и может быть вычислен, если А_d*, А_d** и р* известны; диагонализация А_т то дает его нормализованную диагональную форму А_d, его наибольшее собственное значение κ, и его ортогональная матрица собственных векторов р.

Приложения

Величина ожидания вращения

Матрицы углового переноса (или их диагональные формы) могут использоваться для расчета таких величин, как вращение ожидаемое значение в определенном месте глубоко внутри решетки. Для полной решетки, данной ранее, математическое ожидание спина в центральном узле определяется выражением

${displaystyle leftlangle sigma _{1}ightangle ={frac {1}{Z_{N}}}sum _{all atop spins}sigma _{1}prod _{all atop faces}wleft(sigma _{i},sigma _{j},sigma _{k},sigma _{l}ight).}$

С такими заказанными конфигурациями, что А является блочно-диагональной, как и раньше, мы можем определить 2^м×2^м диагональная матрица

${displaystyle S=left[{egin{array}{cc}I&0�&-Iend{array}}ight],}$

такой, что

${displaystyle leftlangle sigma _{1}ightangle ={frac {{ extrm {tr}}SA^{4}}{{ extrm {tr}}A^{4}}}={frac {{ extrm {tr}}alpha _{m}^{4}PSA^{4}P^{T}}{{ extrm {tr}}alpha _{m}^{4}PA^{4}P^{T}}}={frac {{ extrm {tr}}SA_{d}^{4}}{{ extrm {tr}}A_{d}^{4}}}.}$

Функция разделения на сайт

Еще одна важная величина для решетчатых моделей - это статистическая сумма на узел, вычисляемая в термодинамический предел и написано как

${displaystyle kappa =lim _{Nightarrow infty }left(Z_{N}ight)^{1/N}.}$

В нашем примере это сводится к

${displaystyle kappa =lim _{Nightarrow infty }left(alpha _{m}^{4}{ extrm {tr}}A_{d}^{4}ight)^{1/N}sim alpha _{m}^{4/N},}$

поскольку тр А_d⁴ сходящаяся сумма как м → ∞ и А_d становится бесконечномерным. Кроме того, количество граней 2м(м+1) приближается к количеству сайтов N в термодинамическом пределе, поэтому имеем

${displaystyle alpha _{m}sim kappa ^{mleft(m+1ight)/2},}$

что согласуется с предыдущим уравнением, дающим κ как наибольшее собственное значение для А_т. Другими словами, статистическая сумма на узел задается точно диагонализованным рекурсивным соотношением для угловых матриц переноса в термодинамическом пределе; это позволяет κ быть приближенным с помощью итерационного процесса вычисления А_d для большой решетки.

Однако используемые матрицы экспоненциально растут в размере, и в реальных численных расчетах они должны быть усечены на каждом шаге. Один из способов сделать это - оставить п наибольшие собственные значения на каждом шаге для некоторых фиксированных п. В большинстве случаев последовательность приближений, полученная взятием п = 1,2,3, ... сходится быстро и к точному значению (для точно решаемой модели).

Смотрите также

• Трансферно-матричный метод

Рекомендации

• Бакстер Р. Дж. (1981), "Угловые передаточные матрицы", Physica A, 106 (1–2): 18–27, Bibcode:1981PhyA..106 ... 18B, Дои:10.1016 / 0378-4371 (81) 90203-X
• Бакстер, Р. Дж. (1982), Точно решенные модели в статистической механике, Лондон, Великобритания: Academic Press, ISBN  0-12-083180-5