Ползучесть булыжника - Coble creep
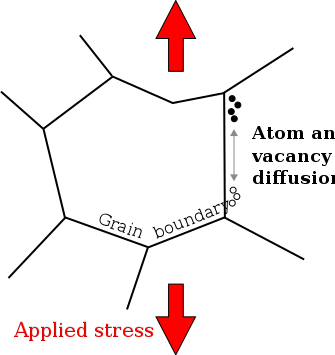
Ползучесть булыжника, форма диффузионная ползучесть, это механизм для деформация из кристаллический твердые вещества. В отличие от других механизмов диффузионной ползучести, ползучесть по Coble похожа на Набарро – Селедочный крап в том, что он преобладает при более низких уровнях напряжения и более высоких температурах, чем механизмы ползучести, использующие скольжение дислокаций.[1] Ползучесть камня происходит за счет диффузии атомов в материале вдоль границы зерен. Этот механизм наблюдается в поликристаллах или вдоль поверхности в монокристалле, что создает чистый поток материала и скольжение границ зерен.
Роберт Л. Кобл впервые изложил свою теорию о том, как материалы слизняк через границы зерен и при высоких температурах в оксиде алюминия. Здесь он, как известно, заметил другой механизм ползучести, который больше зависит от размера зерна.[2]
Скорость деформации в материале, подверженном ползучести по Coble, определяется выражением
куда
- является геометрическим префактором
- приложенное напряжение,
- - средний диаметр зерна,
- - ширина границы зерна,
- - коэффициент диффузии на границе зерен,
- - энергия образования вакансии,
- - энергия активации диффузии вдоль границы зерна
- является Постоянная Больцмана,
- это температура в кельвины
- - атомный объем материала.
Вывод
Ползучесть булыжника, диффузионный механизм, приводится в движение вакансия (или массовый) градиент концентрации. Изменение концентрации вакансий от его равновесного значения дан кем-то
В этом можно убедиться, отметив, что и взяв высокотемпературное расширение, где первый член справа представляет собой концентрацию вакансий от растягивающего напряжения, а второй член представляет собой концентрацию из-за напряжения сжатия. Это изменение концентрации происходит перпендикулярно оси приложенного напряжения, в то время как параллельно напряжению концентрация вакансий не изменяется (из-за того, что разрешенное напряжение и работа равны нулю).[2]
Мы продолжаем, предполагая сферическое зерно, что согласуется с выводом для Набарро-сельдь крап; однако мы преобразуем геометрические константы в константу пропорциональности . Если мы рассмотрим концентрацию вакансий в зерне под действием приложенного растягивающего напряжения, то заметим, что концентрация вакансий на экваторе (перпендикулярном приложенному напряжению) больше, чем на полюсах (параллельно приложенному напряжению). Следовательно, между полюсами и экватором зерна существует поток вакансий. Поток вакансий определяется выражением Первый закон Фика на границе: коэффициент диффузии раз больше градиента концентрации вакансий. Для градиента мы берем среднее значение, определяемое выражением где мы разделили общую разницу концентраций на длину дуги между экватором и полюсом, а затем умножили на ширину границы и длина .
куда - константа пропорциональности. Отсюда отметим, что изменение громкости из-за потока вакансий, диффундирующих из источника площади поток вакансий умножить на атомный объем :
Где второе равенство следует из определения скорости деформации: . Отсюда мы можем узнать скорость деформации:
Где имеет поглощенные константы, а коэффициент диффузии вакансий через границу зерна .
Сравнение с другими механизмами ползучести
Набарро-Селедка
Coble creep и Nabarro-Herring - тесно связанные механизмы. Оба они представляют собой диффузионные процессы, вызванные одним и тем же градиентом концентрации вакансий, происходят в высокотемпературных средах с низким напряжением, и их происхождение аналогично.[1] Для обоих механизмов скорость деформации линейно пропорциональна приложенному напряжению и существует экспоненциальная температурная зависимость. Разница в том, что для ползучести по Коблу массоперенос происходит по границам зерен, тогда как для Набарро-Херринга диффузия происходит через кристалл. Вследствие этого ползучесть по Набарро-Херрингу не зависит от толщины границ зерен и имеет более слабую зависимость от размера зерна. . При ползучести Набарро-Сельдь скорость деформации пропорциональна в отличие от зависимость для ползучести Coble. При рассмотрении чистой скорости диффузионной ползучести сумма обеих скоростей диффузии имеет жизненно важное значение, поскольку они работают в параллельных процессах.
Энергия активации ползучести Набарро-Сельдь, как правило, отличается от энергии активации ползучести Кобла. Это может быть использовано для определения доминирующего механизма. Например, энергия активации для подъема дислокации такая же, как и для набарро-херринга, поэтому, сравнивая температурную зависимость режимов низких и высоких напряжений, можно определить, является ли ползучесть по Коблу или ползучесть по Набарро-Херрингу. [3]
Исследователи обычно используют эти отношения, чтобы определить, какой механизм доминирует в материале; варьируя размер зерна и измеряя влияние на скорость деформации, они могут определить значение в и сделать вывод, является ли ползучесть Кобла или Набарро – Херринга доминирующей.[4]
Ползучесть дислокаций
При умеренном или высоком напряжении доминирующий механизм ползучести перестает быть линейным по приложенному напряжению. . Дислокационная ползучесть, иногда называемая степенной ползучестью (PLC), имеет степенную зависимость от приложенного напряжения в диапазоне от 3 до 8.[1] Движение дислокаций связано с атомной и решеточной структурой кристалла, поэтому разные материалы по-разному реагируют на напряжение, в отличие от ползучести Кобла, которая всегда линейна. Это позволяет легко идентифицировать два механизма, найдя наклон против .
Подъем-скольжение дислокации и ползучесть по Coble вызывают зернограничное скольжение.[1]
Карты механизма деформации
Чтобы понять температурные режимы и режимы напряжений, при которых ползучесть по Coble является доминирующей для материала, полезно взглянуть на карты механизма деформации. Эти карты отображают нормализованное напряжение в зависимости от нормализованной температуры и разграничивают, где конкретные механизмы ползучести являются доминирующими для данного материала и размера зерна (некоторые карты имитируют 3-ю ось, чтобы показать размер зерна). Эти карты следует использовать только в качестве руководства, поскольку они основаны на эвристических уравнениях.[1] Эти карты полезны для определения механизма ползучести, когда рабочие напряжения и температура известны для приложения, определяющего конструкцию материала.
Скольжение границы зерна
Поскольку ползучесть Coble включает в себя перенос массы по границам зерен, в материале могут образовываться трещины или пустоты без надлежащего размещения. Скольжение по границам зерен - это процесс, при котором зерна движутся, чтобы предотвратить разделение на границах зерен.[1] Этот процесс обычно происходит в масштабе времени значительно быстрее, чем процесс распространения массы (на порядок быстрее). Из-за этого скорость зернограничного скольжения обычно не имеет значения для определения процессов в материале. Однако определенные границы зерен, такие как когерентные границы или структурные особенности, препятствующие перемещению границ зерен, могут замедлить скорость проскальзывания границ зерен до точки, где это необходимо учитывать. Процессы, лежащие в основе зернограничного скольжения, аналогичны тем, которые вызывают диффузионную ползучесть.[1]
Этот механизм был первоначально предложен Эшби и Верралом в 1973 году как ползучесть при переключении зерна.[5] Это конкурентоспособно с Coble creep; однако переключение зерен будет преобладать при больших напряжениях, в то время как ползучесть по Коблу будет преобладать при низких напряжениях.
Эта модель предсказывает скорость деформации с пороговой деформацией для переключения зерна. . [1]
Связь с ползучестью по Coble становится понятной, если посмотреть на первый член, который зависит от толщины границ зерен. и обратный размер зерна в кубе .
Рекомендации
- ^ а б c d е ж грамм час Кортни, Томас (2000). Механическое поведение материалов. п. 293-353.
- ^ а б Кобл, Роберт Л. (15 октября 1962 г.). «Модель ползучести, контролируемой диффузией на границе, в поликристаллических материалах». Журнал прикладной физики. Дои:10.1063/1.1702656.
- ^ "MIT OCW 3.22 Механические свойства материалов Весна 2008 PSET 5 Solutions" (PDF).
- ^ Мейерс, Марк Андре; Чавла, Кришан Кумар (2008). Механическое поведение материалов. Издательство Кембриджского университета. С. 555–557.
- ^ М.Ф. Эшби, Р. Верралл, Течение с учетом диффузии и сверхпластичность, Acta Metall. 21 (1973) 149–163, https://doi.org/10.1016/0001-6160(73)90057-6






































