Графики Чанга - Chang graphs
| Графики Чанга | |
|---|---|
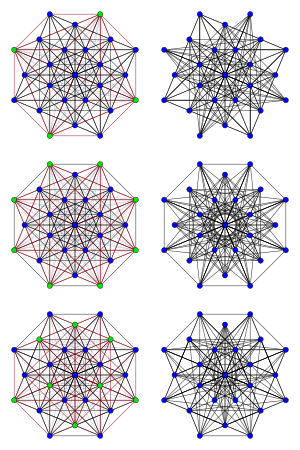 Три графика Чанга (справа) и наборы переключений, генерирующие их из линейный график L(K8) (зеленый, слева) | |
| Вершины | 28 |
| Края | 168 |
| Радиус | 2 |
| Диаметр | 2 |
| Обхват | 3 |
| Автоморфизмы | 96360384 |
| Характеристики | Сильно регулярный |
| Таблица графиков и параметров | |
в математический поле теория графов, то Графики Чанга представляют собой набор из трех 12-обычный неориентированные графы, каждая с 28 вершинами и 168 ребрами. Они есть строго регулярный, с такими же параметрами и спектры как линейный график L(K8) из полный график K8.
Каждый из этих трех графиков может быть получен переключение графиков из L(K8). То есть подмножество S вершин L(K8) выбирается каждое ребро, соединяющее вершину в S с вершиной не в S удален из L(K8), и для каждой пары вершин добавляется ребро (снова одна в S и один не в S), которые еще не были соединены ребром. Среди графов, которые могут быть сгенерированы таким образом, три из них являются графами Чанга.
Графы Чанга названы в честь Чанг Ли-Чиен, который доказал, что, за исключением этих исключений, каждый линейный граф полного графа однозначно определяется своими параметрами как сильно регулярный граф.[1]
Смотрите также
- Граф Шриханде, аналогичное исключение из единственности сильно регулярных графов L(Kп,п)
Рекомендации
- ^ Чанг Ли-Чиен (1959), «Единственность и неединственность треугольных схем ассоциации», Science Record (Пекин), Новый. Сер., 3: 604–613 Cite имеет пустой неизвестный параметр:
|1=(помощь).
