Двунаправленная функция распределения отражательной способности - Bidirectional reflectance distribution function

Диаграмма, показывающая векторы, используемые для определения BRDF. Все векторы имеют единичную длину. ${\displaystyle \omega _{\text{i}}}$ указывает на источник света. ${\displaystyle \omega _{\text{r}}}$ указывает на зрителя (камеру). ${\displaystyle n}$ нормаль к поверхности.

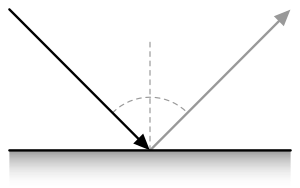
В функция двунаправленного распределения коэффициента отражения (BRDF; ${\displaystyle f_{\text{r}}(\omega _{\text{i}},\,\omega _{\text{r}})}$ ) является функцией четырех вещественных переменных, определяющих, как свет отражается от непрозрачный поверхность. Он используется в оптика реального света, в компьютерная графика алгоритмы, а в компьютерное зрение алгоритмы. Функция принимает направление входящего света, ${\displaystyle \omega _{\text{i}}}$, и исходящее направление, ${\displaystyle \omega _{\text{r}}}$ (взято в системе координат, где нормальная поверхность ${\displaystyle \mathbf {n} }$ лежит вдоль z-axis) и возвращает коэффициент отраженного сияние выходя вместе ${\displaystyle \omega _{\text{r}}}$ к сияние падающий на поверхность со стороны ${\displaystyle \omega _{\text{i}}}$. Каждое направление ${\displaystyle \omega }$ сам по себе параметризованный азимутальный угол ${\displaystyle \phi }$ и зенитный угол ${\displaystyle \theta }$, поэтому BRDF в целом является функцией 4 переменных. В BRDF есть агрегаты sr⁻¹, с стерадианы (SR) быть единицей телесный угол.

Определение

BRDF был впервые определен Фредом Никодемусом примерно в 1965 году.^[1] Определение таково:

${\displaystyle f_{\text{r}}(\omega _{\text{i}},\,\omega _{\text{r}})\,=\,{\frac {\operatorname {d} L_{\text{r}}(\omega _{\text{r}})}{\operatorname {d} E_{\text{i}}(\omega _{\text{i}})}}\,=\,{\frac {\operatorname {d} L_{\text{r}}(\omega _{\text{r}})}{L_{\text{i}}(\omega _{\text{i}})\cos \theta _{\text{i}}\,\operatorname {d} \omega _{\text{i}}}}}$

куда ${\displaystyle L}$ является сияние, или же мощность на единицу телесный угол -в направлении-луча на единицу проектируемая площадь -перпендикулярно лучу, ${\displaystyle E}$ является сияние, или мощность на единицу площадь поверхности, и ${\displaystyle \theta _{\text{i}}}$ угол между ${\displaystyle \omega _{\text{i}}}$ и нормальная поверхность, ${\displaystyle \mathbf {n} }$. Индекс ${\displaystyle {\text{i}}}$ указывает падающий свет, тогда как индекс ${\displaystyle {\text{r}}}$ указывает на отраженный свет.

Причина, по которой функция определяется как отношение двух дифференциалы и не непосредственно как частное между недифференцированными величинами, потому что другой излучающий свет, чем ${\displaystyle \operatorname {d} E_{\text{i}}(\omega _{\text{i}})}$, которые не представляют интереса для ${\displaystyle f_{\text{r}}(\omega _{\text{i}},\,\omega _{\text{r}})}$, может осветить поверхность, что непреднамеренно повлияет на ${\displaystyle L_{\text{r}}(\omega _{\text{r}})}$, в то время как ${\displaystyle \operatorname {d} L_{\text{r}}(\omega _{\text{r}})}$ зависит только от ${\displaystyle \operatorname {d} E_{\text{i}}(\omega _{\text{i}})}$.

Связанные функции

В Функция пространственно изменяющегося двунаправленного распределения отражения (СВБРДФ) - это 6-мерная функция, ${\displaystyle f_{\text{r}}(\omega _{\text{i}},\,\omega _{\text{r}},\,\mathbf {x} )}$, куда ${\displaystyle \mathbf {x} }$ описывает двухмерное местоположение на поверхности объекта.

В Функция двунаправленной текстуры (BTF ) подходит для моделирования неплоских поверхностей и имеет ту же параметризацию, что и SVBRDF; однако, напротив, BTF включает в себя эффекты нелокального рассеяния, такие как затенение, маскирование, взаимное отражение или подповерхностное рассеяние. Таким образом, функции, определяемые BTF в каждой точке поверхности, называются Видимые BRDF.

В Двунаправленная функция распределения отражательной способности поверхностного рассеяния (БССРДФ ), является еще одной обобщенной 8-мерной функцией ${\displaystyle S(\mathbf {x} _{\text{i}},\,\omega _{\text{i}},\,\mathbf {x} _{\text{r}},\,\omega _{\text{r}})}$ в котором свет, попадающий на поверхность, может рассеиваться внутри и выходить в другом месте.

Во всех этих случаях зависимость от длина волны света был проигнорирован. В действительности BRDF зависит от длины волны и учитывает такие эффекты, как переливчатость или же свечение зависимость от длины волны должна быть явной: ${\displaystyle f_{\text{r}}(\lambda _{\text{i}},\,\omega _{\text{i}},\,\lambda _{\text{r}},\,\omega _{\text{r}})}$. Обратите внимание, что в типичном случае, когда все оптические элементы линейный, функция будет подчиняться ${\displaystyle f_{\text{r}}(\lambda _{\text{i}},\,\omega _{\text{i}},\,\lambda _{\text{r}},\,\omega _{\text{r}})=0}$ кроме тех случаев, когда ${\displaystyle \lambda _{\text{i}}=\lambda _{\text{r}}}$: то есть он будет излучать свет только с длиной волны, равной падающему свету. В этом случае его можно параметризовать как ${\displaystyle f_{\text{r}}(\lambda ,\,\omega _{\text{i}},\,\omega _{\text{r}})}$, с одним параметром длины волны.

Физические BRDF

Физически реалистичные BRDF обладают дополнительными свойствами,^[2] включая,

• позитивность: ${\displaystyle f_{\text{r}}(\omega _{\text{i}},\,\omega _{\text{r}})\geq 0}$
• подчиняться Гельмгольц взаимность: ${\displaystyle f_{\text{r}}(\omega _{\text{i}},\,\omega _{\text{r}})=f_{\text{r}}(\omega _{\text{r}},\,\omega _{\text{i}})}$
• экономия энергии: ${\displaystyle \forall \omega _{\text{i}},\,\int _{\Omega }f_{\text{r}}(\omega _{\text{i}},\,\omega _{\text{r}})\,\cos {\theta _{\text{r}}}d\omega _{\text{r}}\leq 1}$

Приложения

BRDF является фундаментальным радиометрический концепция, и соответственно используется в компьютерная графика за фотореалистичный рендеринг синтетических сцен (см. уравнение рендеринга ), а также в компьютерное зрение для многих обратные задачи Такие как распознавание объекта. BRDF также использовался для моделирования светового захвата в солнечные батареи (например, используя Формализм OPTOS ) или низкая концентрация солнечная фотоэлектрическая системы.^[3][4]

В контексте спутникового дистанционного зондирования НАСА использует модель BRDF для характеристики анизотропии отражательной способности поверхности. Для данной площади суши BRDF устанавливается на основе выбранных многоугольных наблюдений отражательной способности поверхности. Хотя отдельные наблюдения зависят от геометрии обзора и солнечного угла, продукт MODIS BRDF / Albedo описывает внутренние свойства поверхности в нескольких спектральных диапазонах с разрешением 500 метров.^[5] Продукт BRDF / Albedo можно использовать для моделирования поверхности. альбедо в зависимости от атмосферного рассеяния.

Модели

BRDF могут быть измерены непосредственно с реальных объектов с помощью откалиброванных камер и источников света;^[6] однако многие феноменологический и аналитические модели были предложены, включая Ламбертовский коэффициент отражения модель часто используется в компьютерной графике. Некоторые полезные функции последних моделей включают:

• приспособление анизотропный отражение
• редактируется с помощью небольшого количества интуитивно понятных параметров
• учет Эффекты Френеля под углом
• хорошо подходит для Методы Монте-Карло.

W. Matusik et al. обнаружили, что интерполяция между измеренными образцами дает реалистичные результаты и проста для понимания.^[7]

Размытый

Глянцевый

Зеркало

Три элементарных компонента, которые можно использовать для моделирования различных взаимодействий света с поверхностью.^[8] Входящий световой луч показан черным, отраженный луч (-ы), смоделированный BRDF, серым.

Некоторые примеры

• Ламбертовская модель, представляющий идеально диффузные (матовые) поверхности постоянным BRDF.
• Ломмель – Силигер, лунное и марсианское отражение.
• Модель отражательной способности Фонга, феноменологическая модель, похожая на пластиковую зеркальность.^[9]
• Модель Блинна – Фонга, напоминая Фонга, но позволяя интерполировать определенные величины, сокращая вычислительные затраты.^[10]
• Модель Торранса – Воробья, общая модель, представляющая поверхности как распределения идеально зеркальных микрограней.^[11]
• Модель Кука – Торранса, модель зеркальных микрограней (Торранс – Воробей), учитывающая длину волны и, следовательно, изменение цвета.^[12]
• Модель палаты, модель зеркально-микрограней с функцией распределения эллиптического гаусса, зависящей от ориентации касательной к поверхности (в дополнение к нормали к поверхности).^[13]
• Модель Орена – Наяра, «направленно-диффузная» модель микрограней с идеально диффузными (а не зеркальными) микрогранями.^[14]
• Ашихмин-Ширли модель, учитывающая анизотропное отражение, наряду с диффузной подложкой под зеркальной поверхностью.^[15]
• HTSG (He, Torrance, Sillion, Greenberg), комплексная физическая модель.^[16]
• Подгоняемая модель Лафортуна, обобщение модели Фонга с множеством зеркальных лепестков, предназначенная для параметрической подгонки измеренных данных.^[17]
• Модель Лебедева для аналитико-сеточного BRDF-приближения.^[18]

Приобретение

Традиционно приборы измерения BRDF называются гониорефлектометры использовать одно или несколько гониометрических рычагов для размещения источника света и детектора в различных направлениях от плоского образца материала, подлежащего измерению. Чтобы измерить полную BRDF, этот процесс необходимо повторить много раз, каждый раз перемещая источник света, чтобы измерить другой угол падения.^[19] К сожалению, использование такого устройства для плотного измерения BRDF занимает очень много времени. Одно из первых усовершенствований этих методов - использование полупрозрачного зеркала и цифровой камеры для одновременного получения множества BRDF-образцов плоской цели. После этой работы многие исследователи разработали другие устройства для эффективного получения BRDF из реальных образцов, и это остается активной областью исследований.

Существует альтернативный способ измерения BRDF на основе HDR изображения. Стандартный алгоритм заключается в измерении облака точек BRDF по изображениям и его оптимизации с помощью одной из моделей BRDF.^[20]

BRDF Производство

Изготовление BRDF относится к процессу создания поверхности на основе измеренной или синтезированной информации целевой BRDF. Существует три способа выполнить такую ​​задачу, но в целом ее можно резюмировать как следующие шаги:

• Измерение или синтез целевого распределения BRDF.
• Выберите это распределение, чтобы дискретизировать его и сделать возможным изготовление.
• Разработайте геометрию, которая производит это распределение (с микрогрань, полутоновое изображение ).
• Оптимизируйте непрерывность и гладкость поверхности по отношению к производственному процессу.

Для изготовления BRDF мишени было предложено множество подходов:

• Фрезерование BRDF: Эта процедура начинается с выборки распределения BRDF и создания его с геометрией микрограней, после чего поверхность оптимизируется с точки зрения гладкости и непрерывности, чтобы соответствовать ограничениям фрезерного станка. Окончательное распределение BRDF - это свертка подложки и геометрия фрезерованной поверхности.^[21]
  

  Последний BRDF - это совокупный эффект выбора геометрии и чернил.
• Печать BRDF: Для создания пространственно изменяющегося BRDF (svBRDF) было предложено использовать отображение гаммы и полутоновое изображение для достижения целевой BRDF. Учитывая набор металлических чернил с известным BRDF, был предложен алгоритм линейного комбинирования их для получения целевого распределения. Пока что печать означает только печать в оттенках серого или цветную, но реальные поверхности могут демонстрировать различную степень зеркальности, которая влияет на их окончательный вид, в результате этот новый метод может помочь нам печатать изображения еще более реалистично.^[22]
• Сочетание чернил и геометрии: В дополнение к цвету и зеркальности объекты реального мира также содержат текстуру. 3D-принтеры можно использовать для создания геометрии и покрытия поверхности подходящими чернилами, оптимальным образом создавая грани и выбирая комбинацию чернил, этот метод может дать нам большую степень свободы в дизайне и более точное изготовление BRDF.^[23]

Смотрите также

• Альбедо
• BSDF
• Гониорефлектометр
• Всплеск оппозиции
• Фотометрия (астрономия)
• Радиометрия
• Отражение
• Приближение Шлика
• Зеркальное отражение

Рекомендации

1. Никодемус, Фред (1965). «Направленное отражение и излучательная способность непрозрачной поверхности». Прикладная оптика. 4 (7): 767–775. Bibcode:1965ApOpt ... 4..767N. Дои:10.1364 / AO.4.000767.
2. Duvenhage, Бернард (2013). «Численная проверка функций распределения двунаправленной отражательной способности на физическую достоверность». Материалы конференции Южноафриканского института компьютерных ученых и информационных технологов. С. 200–208.
3. Эндрюс, Роб У .; Поллард, Эндрю; Пирс, Джошуа М. (2013). «Повышение производительности фотоэлектрической системы с помощью плоских концентраторов без отслеживания: экспериментальные результаты и моделирование на основе BDRF» (PDF). 39-я конференция специалистов по фотоэлектрической технике (PVSC), IEEE, 2013. С. 0229–0234. Дои:10.1109 / PVSC.2013.6744136. ISBN  978-1-4799-3299-3. S2CID  32127698.
4. Andrews, R.W .; Pollard, A .; Пирс, Дж. М., "Повышение производительности фотоэлектрической системы с помощью плоских концентраторов без отслеживания: экспериментальные результаты и моделирование на основе функции двунаправленного отражения (BDRF)," Журнал IEEE по фотогальванике 5 (6), стр. 1626–1635 (2015). DOI: 10.1109 / JPHOTOV.2015.2478064
5. "BRDF / Альбедо". НАСА, Центр космических полетов Годдарда. Получено 9 марта, 2017.
6. Русинкевич, С. "Обзор представления BRDF для компьютерной графики". Получено 2007-09-05.
7. Войцех Матусик, Ханспетер Пфистер, Мэтт Брэнд и Леонард Макмиллан. Модель отражения, управляемая данными. Транзакции ACM на графике. 22 (3) 2002.
8. "Шейдеры наложения слоев mental ray".
9. Фонг Б. Т. Освещение для компьютерных изображений, Сообщения ACM 18 (1975), вып. 6, 311–317.
10. Джеймс Ф. Блинн (1977). «Модели отражения света для изображений, синтезированных на компьютере». Proc. 4-я ежегодная конференция по компьютерной графике и интерактивным технологиям. 11 (2): 192–198. Дои:10.1145/563858.563893. S2CID  8043767.
11. К. Торранс и Э. Воробей. Теория внезеркального отражения от шероховатых поверхностей. J. Optical Soc. Америка, т. 57. 1967. С. 1105–1114.
12. Р. Кук и К. Торранс. «Модель отражательной способности компьютерной графики». Компьютерная графика (Труды SIGGRAPH '81), Vol. 15, № 3, июль 1981 г., стр. 301–316.
13. Уорд, Грегори Дж. (1992). «Измерение и моделирование анизотропного отражения». Труды SIGGRAPH. С. 265–272. Дои:10.1145/133994.134078.
14. С.К. Наяр и М. Орен "Обобщение модели Ламберта и ее значение для машинного зрения ". International Journal on Computer Vision, Vol. 14, No. 3, pp. 227–251, Apr, 1995.
15. Михаил Ашихмин, Питер Ширли, Anisotropic Phong BRDF Model, Journal of Graphics Tools 2000
16. X. Хе, К. Торранс, Ф. Силлон и Д. Гринберг, Комплексная физическая модель отражения света, Компьютерная графика 25 (1991), вып. Ежегодная серия конференций, 175–186.
17. Э. Лафортюн, С. Фу, К. Торранс и Д. Гринберг, Нелинейная аппроксимация функций отражения. В Тернер Уиттед, редактор, SIGGRAPH 97 Conference Proceedings, Annual Conference Series, pp. 117–126. ACM SIGGRAPH, Addison Wesley, август 1997 г.
18. Ильин А., Лебедев А., Синявский В., Игнатенко А., Моделирование отражающих свойств плоских объектов на основе изображений. В архиве 2011-07-06 в Wayback Machine. В: GraphiCon'2009 .; 2009. с. 198-201.
19. Маршнер С.Р., Вестин С.Х., Лафортюн Э.П.Ф., Торранс К.Э., Гринберг Д.П. (1999) Измерение BRDF на основе изображений, включая кожу человека. В: Лищински Д., Ларсон Г.В. (eds) Rendering Techniques ’99. Eurographics. Шпрингер, Вена
20. Проект BRDFRecon В архиве 2011-07-06 в Wayback Machine
21. Вейрих, Тим; Пирс, Питер; Матусик, Войцех; Русинкевич, Шимон (2009). «Изготовление микрогеометрии для нестандартной отражательной способности поверхности» (PDF). ACM SIGGRAPH 2009 Статьи на - SIGGRAPH '09. Нью-Йорк, Нью-Йорк, США: ACM Press: 1. Дои:10.1145/1576246.1531338. ISBN  9781605587264. S2CID  13932018.
22. Матусик, Войцех; Айдин, Борис; Гу, Цзиньвэй; Лоуренс, Джейсон; Lensch, Hendrik P.A .; Пеллачини, Фабио; Русинкевич, Шимон (01.12.2009). «Печать с пространственно-переменным коэффициентом отражения». Транзакции ACM на графике. 28 (5): 1–9. Дои:10.1145/1618452.1618474.
23. Лань, Яньсян; Донг, Юэ; Пеллачини, Фабио; Тонг, Синь (01.07.2013). «Изготовление двухуровневого внешнего вида». Транзакции ACM на графике. 32 (4): 1–12. Дои:10.1145/2461912.2461989. ISSN  0730-0301. S2CID  4960068.

дальнейшее чтение

• Любин, Дэн; Роберт Массом (10 февраля 2006 г.). Полярное дистанционное зондирование. Том I: Атмосфера и океаны (1-е изд.). Springer. п. 756. ISBN  978-3-540-43097-1.
• Мэтт, Фарр; Грег Хамфрис (2004). Физический рендеринг (1-е изд.). Морган Кауфманн. п. 1019. ISBN  978-0-12-553180-1.
• Schaepman-Strub, G .; М. Э. Шепман; Т. Х. Пейнтер; С. Дангель; Ю. В. Мартончик (15.07.2006). «Величины отражения в оптическом дистанционном зондировании: определения и тематические исследования». Дистанционное зондирование окружающей среды. 103 (1): 27–42. Bibcode:2006RSEnv.103 ... 27S. Дои:10.1016 / j.rse.2006.03.002.

• Интуитивно понятное введение в концепцию модели отражения и BRDF.