Граф Барнетта – Босака – Ледерберга - Barnette–Bosák–Lederberg graph
| Граф Барнетта – Босака – Ледерберга | |
|---|---|
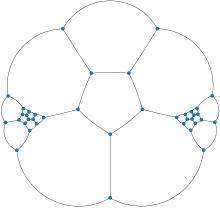 | |
| Вершины | 38 |
| Края | 57 |
| Радиус | 5 |
| Диаметр | 9 |
| Обхват | 4 |
| Хроматическое число | 3 |
| Хроматический индекс | 3 |
| Характеристики | Кубический Планарный Многогранник |
| Таблица графиков и параметров | |
в математический поле теория графов, то Граф Барнетта – Босака – Ледерберга это кубический (то есть 3-обычный ) многогранный граф без Гамильтонов цикл, наименьший возможный такой граф.[1] Он был открыт в середине 1960-х гг. Джошуа Ледерберг, Дэвид Барнетт и Юрай Босак, в честь которых он назван. У него 38 вершин и 69 ребер.[2][3][4]
Другие большие негамильтоновы кубические многогранные графы включают 46-вершинный График Тутте и граф с 44 вершинами, найденный Эмануэль Гринбергс с помощью Теорема Гринберга.Граф Барнетта – Босака – Ледерберга имеет аналогичную конструкцию графу Тутте, но состоит из двух фрагментов Тутте, соединенных пятиугольная призма, вместо трех, подключенных через тетраэдр Без ограничения на наличие ровно трех ребер в каждой вершине возможны гораздо меньшие негамильтоновы многогранные графы, включая График Гольднера – Харари и Граф Гершеля.
Рекомендации
- ^ Холтон, Д. А .; Маккей, Б.Д. (1988), «Наименьшие негамильтоновы 3-связные кубические плоские графы имеют 38 вершин», Журнал комбинаторной теории, серия B, 45 (3): 305–319, Дои:10.1016/0095-8956(88)90075-5
- ^ Ледерберг, Джошуа (1967), "Схемы Гамильтона выпуклых трехвалентных многогранников (до 18 вершин)", Американский математический ежемесячник, 74: 522–527, Дои:10.2307/2314879, МИСТЕР 0211895
- ^ Босак, J. (1967), "Гамильтоновы линии в кубических графах", Теория графов (Международные симпозиумы, Рим, 1966 г.), Нью-Йорк: Гордон и Брич, стр. 35–46, МИСТЕР 0221970
- ^ Вайсштейн, Эрик В. "График Барнетта-Босака-Ледерберга". MathWorld.
