Алгоритм альфа макс плюс бета мин - Alpha max plus beta min algorithm
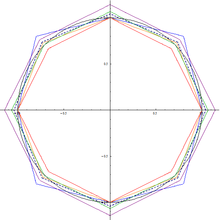
В алгоритм альфа макс плюс бета мин представляет собой высокоскоростное приближение квадратный корень суммы двух квадратов. Квадратный корень из суммы двух квадратов, также известный как Пифагорейское сложение, полезная функция, потому что она находит гипотенуза прямоугольного треугольника с учетом длины двух сторон, норма 2-D вектор, или величина из комплексное число z = а + бя дал настоящий и воображаемый части.
Алгоритм избегает выполнения операций извлечения квадратного корня и извлечения квадратного корня, вместо этого используются простые операции, такие как сравнение, умножение и сложение. Некоторые варианты выбора параметров α и β алгоритма позволяют свести операцию умножения к простому сдвигу двоичных цифр, что особенно хорошо подходит для реализации в высокоскоростных цифровых схемах.
Приближение выражается как
куда - максимальное абсолютное значение а и б, и - минимальное абсолютное значение а и б.
Для наиболее близкого приближения оптимальные значения для и находятся и , что дает максимальную ошибку 3,96%.
| Наибольшая ошибка (%) | Средняя ошибка (%) | ||
|---|---|---|---|
| 1/1 | 1/2 | 11.80 | 8.68 |
| 1/1 | 1/4 | 11.61 | 3.20 |
| 1/1 | 3/8 | 6.80 | 4.25 |
| 7/8 | 7/16 | 12.50 | 4.91 |
| 15/16 | 15/32 | 6.25 | 3.08 |
| 3.96 | 2.41 |

Улучшения
Когда , становится меньше, чем (что геометрически невозможно) вблизи осей, где близка к нулю. Это можно исправить, заменив результат на всякий раз, когда это больше, по существу разделяя линию на два разных сегмента.
В зависимости от оборудования это улучшение может быть почти бесплатным.
Использование этого улучшения изменяет оптимальные значения параметров, поскольку им больше не требуется точное соответствие для всего интервала. Более низкий и выше таким образом может еще больше повысить точность.
Повышение точности: При таком разделении линии на две можно было бы еще больше повысить точность, заменив первый сегмент более точной оценкой, чем , и отрегулируйте и соответственно.
| Наибольшая ошибка (%) | ||||
|---|---|---|---|---|
| 1 | 0 | 7/8 | 17/32 | −2.65% |
| 1 | 0 | 29/32 | 61/128 | +2.4% |
| 1 | 1/8 | 7/8 | 33/64 | −1.7% |
| 1 | 5/32 | 27/32 | 71/128 | 1.22% |
| 127/128 | 3/16 | 27/32 | 71/128 | −1.13% |
Однако помните, что ненулевое значение потребует по крайней мере одного дополнительного сложения и некоторых битовых сдвигов (или умножения), что, вероятно, почти удвоит стоимость и, в зависимости от оборудования, возможно, в первую очередь лишит цели использования приближения.
Смотрите также
- Гипотеза, точная функция или алгоритм, который также защищен от переполнения и потери значимости.
Рекомендации
- Лайонс, Ричард Дж.. Понимание цифровой обработки сигналов, раздел 13.2. Прентис Холл, 2004 ISBN 0-13-108989-7.
- Гриффин, Грант. Уловка DSP: оценщик величины.
внешняя ссылка
- «Расширение до трех измерений». Обмен стеком. 14 мая 2015 года.




















