Активная и пассивная трансформация - Active and passive transformation

Относительно понятия «пассивного преобразования» в грамматике см. активный залог и пассивный залог.

В активном преобразовании (слева) точка перемещается из положения P в P 'путем поворота по часовой стрелке на угол θ относительно начала системы координат. В пассивном преобразовании (справа) точка P не перемещается, а система координат вращается против часовой стрелки на угол θ относительно своего начала. Координаты P 'в активном случае (то есть относительно исходной системы координат) такие же, как координаты P относительно повернутой системы координат.

В аналитическая геометрия, пространственные преобразования в 3-мерном евклидовом пространстве ${\displaystyle \mathbb {R} ^{3}}$ подразделяются на активный или трансформации алиби, и пассивный или преобразования псевдонимов. An активное преобразование^[1] это трансформация который фактически изменяет физическое положение (алиби, в другом месте) точки, или жесткое тело, который можно определить при отсутствии система координат; тогда как пассивное преобразование^[2] просто изменение системы координат, в которой описывается объект (псевдоним, другое имя) (изменение карты координат или изменение основы ). От трансформация, математики обычно относятся к активным преобразованиям, а физики и инженеры может означать и то, и другое. Оба типа преобразования могут быть представлены комбинацией перевод и линейное преобразование.

Другими словами, пассивный преобразование относится к описанию такой же объект в двух разных системах координат.^[3]С другой стороны, активное преобразование представляет собой преобразование одного или нескольких объектов относительно одной и той же системы координат. Например, активные преобразования полезны для описания последовательных положений твердого тела. С другой стороны, пассивные преобразования могут быть полезны при анализе движения человека для наблюдения за движением большеберцовая кость относительно бедренная кость, то есть его движение относительно a (местный) система координат, которая движется вместе с бедренной костью, а не (Глобальный) система координат, которая крепится к полу.^[3]

пример

Вращение рассматривается как пассивное (псевдоним) или активный (алиби) преобразование

Перевод и вращение как пассивные (псевдоним) или активный (алиби) преобразования

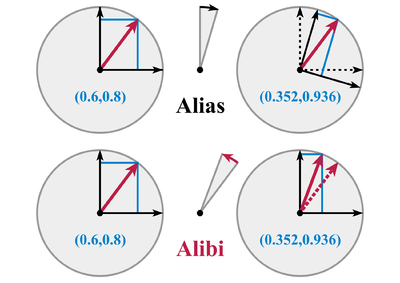
В качестве примера пусть вектор ${\displaystyle \mathbf {v} =(v_{1},v_{2})\in \mathbb {R} ^{2}}$, - вектор на плоскости. Поворот вектора на угол θ против часовой стрелки задается матрица вращения:

${\displaystyle R={\begin{pmatrix}\cos \theta &-\sin \theta \\\sin \theta &\cos \theta \end{pmatrix}},}$

который можно рассматривать либо как активное преобразование или пассивное преобразование (где указанная выше матрица будет инвертирована), как описано ниже.

Пространственные преобразования в евклидовом пространстве ${\displaystyle \mathbb {R} ^{3}}$

В общем пространственная трансформация ${\displaystyle T\colon \mathbb {R} ^{3}\to \mathbb {R} ^{3}}$ может состоять из перевода и линейного преобразования. В дальнейшем перевод будет опущен, а линейное преобразование будет представлено матрицей 3 × 3 ${\displaystyle T}$.

Активная трансформация

Как активное преобразование, ${\displaystyle T}$ преобразует исходный вектор ${\displaystyle \mathbf {v} =(v_{x},v_{y},v_{z})}$ в новый вектор ${\displaystyle \mathbf {v} '=(v'_{x},v'_{y},v'_{z})=T\mathbf {v} =T(v_{x},v_{y},v_{z})}$.

Если посмотреть ${\displaystyle \{\mathbf {e} '_{x}=T(1,0,0),\ \mathbf {e} '_{y}=T(0,1,0),\ \mathbf {e} '_{z}=T(0,0,1)\}}$ в качестве новой основы, то координаты нового вектора ${\displaystyle \mathbf {v} '=v_{x}\mathbf {e} '_{x}+v_{y}\mathbf {e} '_{y}+v_{z}\mathbf {e} '_{z}}$ в новой основе такие же, как у ${\displaystyle \mathbf {v} =v_{x}\mathbf {e} _{x}+v_{y}\mathbf {e} _{y}+v_{z}\mathbf {e} _{z}}$ в исходной основе. Обратите внимание, что активные преобразования имеют смысл даже как линейное преобразование в другое векторное пространство. Имеет смысл записывать новый вектор в базисе без штриха (как указано выше), только когда преобразование происходит из пространства в себя.

Пассивное преобразование

С другой стороны, при просмотре ${\displaystyle T}$ как пассивное преобразование начальный вектор ${\displaystyle \mathbf {v} =(v_{x},v_{y},v_{z})}$ остается неизменной, а система координат и ее базисные векторы преобразуются в обратном направлении, то есть с обратным преобразованием ${\displaystyle T^{-1}}$.^[4] Это дает новую систему координат XYZ с базисными векторами:

${\displaystyle \mathbf {e} _{X}=T^{-1}(1,0,0),\ \mathbf {e} _{Y}=T^{-1}(0,1,0),\ \mathbf {e} _{Z}=T^{-1}(0,0,1)}$

Новые координаты ${\displaystyle (v_{X},v_{Y},v_{Z})}$ из ${\displaystyle \mathbf {v} }$ относительно новой системы координат XYZ задаются формулами:

${\displaystyle \mathbf {v} =(v_{x},v_{y},v_{z})=v_{X}e_{X}+v_{Y}e_{Y}+v_{Z}e_{Z}=T^{-1}(v_{X},v_{Y},v_{Z})}$.

Из этого уравнения видно, что новые координаты задаются

${\displaystyle (v_{X},v_{Y},v_{Z})=T(v_{x},v_{y},v_{z})}$.

Как пассивное преобразование ${\displaystyle T}$ преобразует старые координаты в новые.

Обратите внимание на эквивалентность между двумя видами преобразований: координаты новой точки в активном преобразовании и новые координаты точки в пассивном преобразовании одинаковы, а именно

${\displaystyle (v_{X},v_{Y},v_{Z})=(v'_{x},v'_{y},v'_{z})}$.

Смотрите также

• Смена основы
• Ковариация и контравариантность векторов
• Вращение осей
• Перевод осей

использованная литература

1. Вайсштейн, Эрик В. «Преобразование Алиби». Материал из MathWorld - веб-ресурса Wolfram.
2. Вайсштейн, Эрик В. «Преобразование псевдонима». Материал из MathWorld - веб-ресурса Wolfram.
3. Джозеф К. Дэвидсон, Кеннет Хендерсон Хант (2004). «§4.4.1 Активная интерпретация и активное преобразование». Роботы и теория винта: приложения кинематики и статики к робототехнике. Издательство Оксфордского университета. п. 74 ff. ISBN  0-19-856245-4.
4. Амидрор, Исаак (2007). «Приложение D: Замечание D.12». Теория феномена муара: апериодические слои. Springer. п. 346. ISBN  978-1-4020-5457-0.

• Дирк Струик (1953) Лекции по аналитической и проективной геометрии, стр. 84, Эддисон-Уэсли.

внешние ссылки

• Неоднозначность пользовательского интерфейса