Проблема удовлетворения взвешенных ограничений - Weighted constraint satisfaction problem

В искусственный интеллект и исследование операций, а Проблема удовлетворения взвешенных ограничений (WCSP) является обобщением проблема удовлетворения ограничений (CSP) где некоторые из ограничения могут быть нарушены (по степени нарушения) и в которых предпочтения среди решений могут быть выражены. Это обобщение позволяет представить больше реальных проблем, в частности тех, которые чрезмерно ограничены (невозможно найти решение без нарушения хотя бы одного ограничения), или тех, для которых мы хотим найти решение с минимальными затратами (согласно а функция стоимости ) среди множества возможных решений.

Формальное определение

Сеть взвешенных ограничений (WCN) - это триплет ${\displaystyle \langle X,C,k\rangle }$ куда ${\displaystyle X}$ конечный набор переменных, ${\displaystyle C}$ - конечный набор мягких ограничений и ${\displaystyle k>0}$ является либо натуральным целым числом, либо ${\displaystyle \infty }$.

Каждое мягкое ограничение ${\displaystyle c_{S}\in C}$ включает упорядоченный набор ${\displaystyle S}$ переменных, называемых его областью видимости, и определяется как функция стоимости из ${\displaystyle l(S)}$ к ${\displaystyle \langle 0,...,k\rangle }$ куда ${\displaystyle l(S)}$ это набор возможных экземпляров ${\displaystyle S}$. Когда создание ${\displaystyle I\in l(S)}$ дана стоимость ${\displaystyle k}$, т.е. ${\displaystyle c_{S}(I)=k}$, говорят, запрещено. В противном случае это разрешено с соответствующей стоимостью (0 - вполне удовлетворительно).

В WCSP, конкретном подклассе Valued CSP (VCSP), затраты объединяются с конкретным оператором. ${\displaystyle \oplus }$ определяется как: ${\displaystyle \forall \alpha ,\beta \in \langle 0,...,k\rangle ,\alpha \oplus \beta =min(k,\alpha +\beta )}$. Частичная инверсия ${\displaystyle \oplus }$ является ${\displaystyle \ominus }$ определяется: если ${\displaystyle 0\leq \beta \leq \alpha <k}$, ${\displaystyle \alpha \ominus \beta =\alpha -\beta }$ и если ${\displaystyle 0\leq \beta <k}$, ${\displaystyle k\ominus \beta =k}$.

Без потери общности существование нулевого ограничения ${\displaystyle c_{\emptyset }}$ (стоимость), а также наличие унарного ограничения ${\displaystyle c_{x}}$ для каждой переменной ${\displaystyle x}$ предполагается.

Общая стоимость создания экземпляра ${\displaystyle I\in l(S)}$ на мягком принуждении ${\displaystyle c_{S}}$, включает стоимость ${\displaystyle I}$ на ${\displaystyle c_{S}}$ а также нулевую стоимость ${\displaystyle c_{\emptyset }}$ и унарные затраты на ${\displaystyle I}$ переменных в ${\displaystyle S}$.

Рассматривая WCN, обычная (NP-трудная) задача WCSP - найти полный экземпляр с минимальными затратами.

Разрешение двоичных / троичных WCSP

Подход с операциями переноса затрат

Согласованность узлов (NC) и согласованность дуги (AC), введенные для задачи удовлетворения ограничений (CSP), были изучены позже в контексте WCSP. Кроме того, было предложено несколько согласований относительно лучшей формы согласованности дуги: Полная согласованность дуги (FDAC),^[1] Согласованность экзистенциальной направленной дуги (EDAC),^[2] Согласованность виртуальной дуги (VAC)^[3] и Оптимальная консистенция мягкой дуги (OSAC).^[4]

Алгоритмы, обеспечивающие такие свойства, основаны на преобразованиях с сохранением эквивалентности (EPT), которые позволяют безопасно перемещать затраты между ограничениями. Три основных операции по переносу затрат:

• Проект: перенос затрат с ограничений на унарные ограничения
• ProjectUnary: перенос стоимости с унарного ограничения на нулевое ограничение
• Расширение: перенос стоимости от унарного ограничения к ограничению

Основные преобразования, сохраняющие эквивалентность.

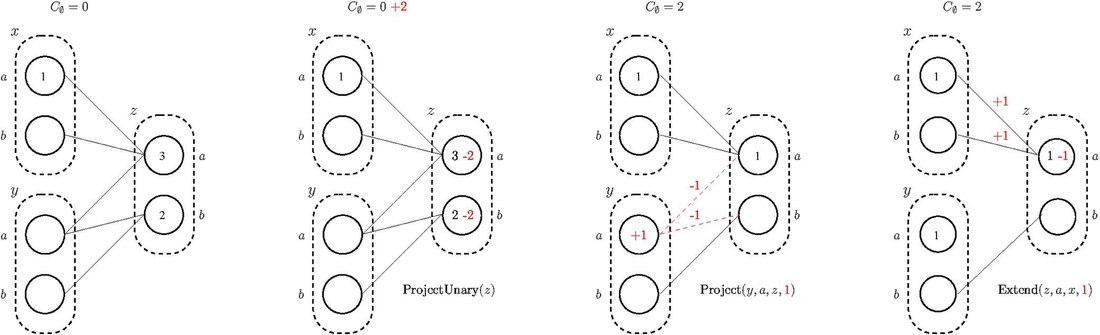
Цель преобразований с сохранением эквивалентности - сконцентрировать затраты на нулевом ограничении. ${\displaystyle c_{\emptyset }}$ и эффективно удалять экземпляры и значения с добавленной стоимостью, добавленной к ${\displaystyle c_{\emptyset }}$, которая больше или равна запрещенной стоимости или стоимости найденного лучшего решения.

Подход без операций по переносу затрат

Альтернативой алгоритмам переноса затрат является алгоритм PFC-MRDAC^[5] который является классическим алгоритмом ветвей и границ, который вычисляет нижнюю границу ${\displaystyle lb}$ в каждом узле дерева поиска, что соответствует недооценке стоимости любого решения, которое может быть получено из этого узла. Стоимость лучшего найденного решения составляет ${\displaystyle ub}$. Когда ${\displaystyle lb\geq ub}$, то дерево поиска с этого узла обрезается.

Разрешение n-арных WCSP

Было показано, что алгоритмы переноса стоимости особенно эффективны для решения реальных проблем, когда мягкие ограничения являются двоичными или троичными (максимальная арность ограничений в задаче равна 2 или 3). Для мягких ограничений большой арности перенос стоимости становится серьезная проблема, потому что риск комбинаторный взрыв нужно контролировать.

Алгоритм, называемый ${\displaystyle GAC^{w}-WSTR}$,^[6] был предложен для применения слабой версии свойства Generalized Arc Consistency (GAC) к мягким ограничениям, определяемым расширенно путем перечисления кортежей и их стоимости. Этот алгоритм сочетает в себе два метода, а именно: Простое табличное сокращение (STR)^[7] и перевод стоимости. Выявляются значения, которые больше не согласуются с GAC, и вычисляются минимальные затраты на значения. Это особенно полезно для эффективного выполнения операций прогнозирования, необходимых для создания GAC.

Контрольные точки

Многие реальные тесты WCSP доступны на http://costfunction.org/en/benchmark^[8] и дальше http://www.cril.univ-artois.fr/~lecoutre/benchmarks.html.

Смотрите также

• Проблема удовлетворения ограничений
• Ограниченное программирование
• Планирование на основе предпочтений

Рекомендации

1. М. Купер. Операции редукции при удовлетворении нечетких или оцененных ограничений. Нечеткие множества и системы, 134 (3): 311–342, 2003.
2. С. де Живри, Ф. Герас, М. Зитницки и Дж. Ларроса. Постоянная стабильность дуги: приближение к полной согласованности дуги в взвешенных CSP. В трудах IJCAI ’05, страницы 84–89, 2005 г.
3. М. Купер, С. де Живри, М. Санчес, Т. Шикс, М. Зитницки. Согласованность виртуальной дуги для взвешенного CSP. В трудах AAAI ’08, страницы 253–258, 2008 г.
4. М. Купер, С. де Живри, М. Санчес, Т. Шикс, М. Зитницки и Т. Вернер. Еще раз о стабильности мягкой дуги. Искусственный интеллект, 174 (7-8): 449–478, 2010.
5. Э.К. Фрейдер и Р.Дж. Уоллес. Частичное удовлетворение ограничений. Искусственный интеллект, 58 (1-3): 21–70, 1992.
6. К. Лекутр, Н. Пэрис, О. Руссель, С. Табари. Распространение ограничений мягкой таблицы. In Proceedings of CP’12, pages 390-405, 2012.
7. К. Лекутр. STR2: Оптимизированное простое сокращение таблицы для ограничения таблицы. Ограничения, 16 (4): 341–371, 2011.
8. Целью этого веб-сайта является продвижение сети функций стоимости в предоставлении контрольных и обучающих материалов, демонстрации решателя, ссылки на статью о функции стоимости, используемой в контексте программирования с ограничениями.