Система переменной массы - Variable-mass system

Ракеты, которые теряют значительное количество массы в качестве топлива во время полета, являются примером системы с переменной массой.

В механика, а система переменной массы это собрание дело чей масса варьируется в зависимости от время. Попытка применить Второй закон Ньютона движения непосредственно в такую ​​систему.^[1][2] Вместо этого зависимость массы от времени м можно вычислить, переставив второй закон Ньютона и добавив член для учета импульс осуществляется массовым входом в систему или выходом из нее. Общее уравнение движения переменной массы записывается как

${\displaystyle \mathbf {F} _{\mathrm {ext} }+\mathbf {v} _{\mathrm {rel} }{\frac {\mathrm {d} m}{\mathrm {d} t}}=m{\mathrm {d} \mathbf {v} \over \mathrm {d} t}}$

где F_доб это чистая внешняя сила на теле, v_rel это относительная скорость убегающей или входящей массы по отношению к центр массы тела, и v это скорость тела.^[3] В астродинамика, посвященный механике ракеты, период, термин v_rel часто называют эффективная скорость истечения и обозначен v_е.^[4]

Вывод

Существуют разные выводы для уравнения движения системы с переменной массой, в зависимости от того, входит ли масса в тело или выходит из него (другими словами, увеличивается или уменьшается масса движущегося тела соответственно). Для упрощения расчетов все тела рассматриваются как частицы. Также предполагается, что масса не способна воздействовать на тело внешними силами вне периодов аккреции / абляции.

Прирост массы

В момент 1 масса dм с относительной скоростью ты вот-вот столкнется с основной массой м и скорость v. Через время dт, в момент 2 обе частицы движутся как одно тело со скоростью v + dv.

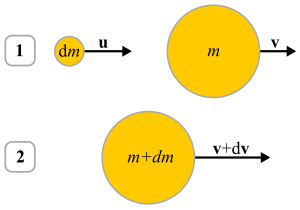
Следующий вывод предназначен для тела, которое набирает массу (нарастание ). Тело с изменяющейся во времени массой м движется со скоростью v в начальное время т. В этот же момент частица массы dm движется со скоростью ты. Начальный импульс можно записать как^[5]

${\displaystyle \mathbf {p} _{\mathrm {1} }=m\mathbf {v} +\mathbf {u} \mathrm {d} m}$

Сейчас за раз т + dт, пусть и основное тело, и частица срастаются в тело скорости v + dv. Таким образом, новый импульс системы можно записать как

${\displaystyle \mathbf {p} _{\mathrm {2} }=(m+\mathrm {d} m)(\mathbf {v} +\mathrm {d} \mathbf {v} )=m\mathbf {v} +m\mathrm {d} \mathbf {v} +\mathbf {v} \mathrm {d} m+\mathrm {d} m\mathrm {d} \mathbf {v} }$

Поскольку dмdv является произведением двух малых значений, его можно игнорировать, то есть в течение dт импульс системы меняется при

${\displaystyle \mathrm {d} \mathbf {p} =\mathbf {p} _{\mathrm {2} }-\mathbf {p} _{\mathrm {1} }=(m\mathbf {v} +m\mathrm {d} \mathbf {v} +\mathbf {v} \mathrm {d} m)-(m\mathbf {v} +\mathbf {u} \mathrm {d} m)=m\mathrm {d} \mathbf {v} -(\mathbf {u} -\mathbf {v} )\mathrm {d} m}$

Следовательно, по Второй закон Ньютона

${\displaystyle \mathbf {F} _{\mathrm {ext} }={\frac {\mathrm {d} \mathbf {p} }{\mathrm {d} t}}={\frac {m\mathrm {d} \mathbf {v} -(\mathbf {u} -\mathbf {v} )\mathrm {d} m}{\mathrm {d} t}}=m{\frac {\mathrm {d} \mathbf {v} }{\mathrm {d} t}}-(\mathbf {u} -\mathbf {v} ){\frac {\mathrm {d} m}{\mathrm {d} t}}}$

Отмечая, что ты - v - скорость dм относительный к м, обозначается как v_rel, это окончательное уравнение можно представить в виде^[6]

${\displaystyle \mathbf {F} _{\mathrm {ext} }+\mathbf {v} _{\mathrm {rel} }{\frac {\mathrm {d} m}{\mathrm {d} t}}=m{\mathrm {d} \mathbf {v} \over \mathrm {d} t}}$

Массовая абляция / выброс

В системе, где масса выбрасывается или удален от основного корпуса происхождение немного отличается. Вовремя т, пусть масса м путешествовать со скоростью v, что означает, что начальный импульс системы равен

${\displaystyle \mathbf {p} _{\mathrm {1} }=m\mathbf {v} }$

Предполагая ты быть скоростью уносимой массы dм по отношению к земле, за раз т + dт импульс системы становится

${\displaystyle \mathbf {p} _{\mathrm {2} }=(m-\mathrm {d} m)(\mathbf {v} +\mathrm {d} \mathbf {v} )-\mathbf {u} \mathrm {d} m=m\mathbf {v} +m\mathrm {d} \mathbf {v} -\mathbf {v} \mathrm {d} m-\mathrm {d} m\mathrm {d} \mathbf {v} -\mathbf {u} \mathrm {d} m}$

где ты - это скорость выброшенной массы по отношению к земле; она отрицательна, потому что уносимая масса движется в направлении, противоположном массе. Таким образом, в течение dт импульс системы меняется при

${\displaystyle \mathrm {d} \mathbf {p} =\mathbf {p} _{\mathrm {2} }-\mathbf {p} _{\mathrm {1} }=(m\mathbf {v} +m\mathrm {d} \mathbf {v} -\mathrm {d} \mathbf {m} \mathrm {d} \mathbf {v} -\mathbf {v} \mathrm {d} m-\mathbf {u} \mathrm {d} m)-(m\mathbf {v} )=m\mathrm {d} \mathbf {v} -(\mathbf {v} +\mathrm {d} \mathbf {v} +\mathbf {u} )\mathrm {d} m}$

Относительная скорость v_rel абляции массы по отношению к массе м записывается как

${\displaystyle \mathbf {v} _{\mathrm {rel} }=\mathbf {u} -(-\mathbf {v} -\mathrm {d} \mathbf {v} )=\mathbf {v} +\mathrm {d} \mathbf {v} +\mathbf {u} }$

Поэтому изменение импульса можно записать как

${\displaystyle \mathrm {d} \mathbf {p} =m\mathrm {d} \mathbf {v} -\mathbf {v} _{\mathrm {rel} }\mathrm {d} m}$

Следовательно, по Второй закон Ньютона

${\displaystyle \mathbf {F} _{\mathrm {ext} }={\frac {\mathrm {d} \mathbf {p} }{\mathrm {d} t}}={\frac {m\mathrm {d} \mathbf {v} -\mathbf {v} _{\mathrm {rel} }\mathrm {d} m}{\mathrm {d} t}}=m{\frac {\mathrm {d} \mathbf {v} }{\mathrm {d} t}}-\mathbf {v} _{\mathrm {rel} }{\frac {\mathrm {d} m}{\mathrm {d} t}}}$

Поэтому окончательное уравнение можно представить в виде

${\displaystyle \mathbf {F} _{\mathrm {ext} }+\mathbf {v} _{\mathrm {rel} }{\frac {\mathrm {d} m}{\mathrm {d} t}}=m{\mathrm {d} \mathbf {v} \over \mathrm {d} t}}$

Формы

Когда выпущен, эта ракета воздушный шар выбрасывает значительную часть своей массы в виде воздуха, вызывая большое ускорение.

По определению ускорение, а = dv/ дт, поэтому уравнение движения системы с переменной массой можно записать в виде

${\displaystyle \mathbf {F} _{\mathrm {ext} }+\mathbf {v} _{\mathrm {rel} }{\frac {\mathrm {d} m}{\mathrm {d} t}}=m\mathbf {a} }$

В телах, которые не рассматриваются как частицы а должен быть заменен на а_см, ускорение центр массы системы, то есть

${\displaystyle \mathbf {F} _{\mathrm {ext} }+\mathbf {v} _{\mathrm {rel} }{\frac {\mathrm {d} m}{\mathrm {d} t}}=m\mathbf {a} _{\mathrm {cm} }}$

Часто сила из-за толкать определяется как ${\displaystyle \mathbf {F} _{\mathrm {thrust} }=\mathbf {v} _{\mathrm {rel} }{\frac {\mathrm {d} m}{\mathrm {d} t}}}$ так что

${\displaystyle \mathbf {F} _{\mathrm {ext} }+\mathbf {F} _{\mathrm {thrust} }=m\mathbf {a} _{\mathrm {cm} }}$

Эта форма показывает, что тело может иметь ускорение за счет тяги, даже если на него не действуют внешние силы (F_доб = 0). Наконец, обратите внимание, что если позволить F_сеть быть суммой F_доб и F_{толкать} тогда уравнение приобретает обычную форму второго закона Ньютона:

${\displaystyle \mathbf {F} _{\mathrm {net} }=m\mathbf {a} _{\mathrm {cm} }}$

Уравнение идеальной ракеты

Ракета массовые отношения от конечной скорости, рассчитанной из уравнения ракеты

Основная статья: Уравнение ракеты Циолковского

В уравнение идеальной ракеты, или Циолковский уравнение ракеты, можно использовать для изучения движения транспортных средств, которые ведут себя как ракета (где тело ускоряется за счет выброса части своей массы, пропеллент, с высокой скоростью). Его можно вывести из общего уравнения движения для систем с переменной массой следующим образом: когда на тело не действуют внешние силы (F_доб = 0) уравнение движения системы с переменной массой сводится к^[2]

${\displaystyle \mathbf {v} _{\mathrm {rel} }{\frac {\mathrm {d} m}{\mathrm {d} t}}=m{\frac {\mathrm {d} \mathbf {v} }{\mathrm {d} t}}}$

Если скорость выброшенного пороха, v_rel, предполагается, имеет направление, противоположное ускорению ракеты, dv/ дт, то скаляр эквивалент этого уравнения можно записать как

${\displaystyle -v_{\mathrm {rel} }{\frac {\mathrm {d} m}{\mathrm {d} t}}=m{\mathrm {d} v \over \mathrm {d} t}}$

откуда dт можно отменить, чтобы дать

${\displaystyle -v_{\mathrm {rel} }\mathrm {d} m=m\mathrm {d} v\,}$

Интеграция разделение переменных дает

${\displaystyle -v_{\mathrm {rel} }\int _{m_{0}}^{m_{1}}{\frac {\mathrm {d} m}{m}}=\int _{v_{0}}^{v_{1}}\mathrm {d} v}$

${\displaystyle v_{\mathrm {rel} }\ln {\frac {m_{0}}{m_{1}}}=v_{1}-v_{0}}$

Переставляя и позволяя Δv = v₁ - v₀, приходим к стандартной форме уравнения идеальной ракеты:

${\displaystyle \Delta v=v_{\mathrm {rel} }\ln {\frac {m_{0}}{m_{1}}}}$

где м₀ - начальная полная масса, включая топливо, м₁ окончательная общая масса, v_rel это эффективная скорость истечения (часто обозначается как v_е), а Δv - максимальное изменение скорости автомобиля (при отсутствии внешних сил).

использованная литература

1. Клеппнер, Д.; Коленков, Р. Дж. (1978) [1973]. Введение в механику. Лондон: Макгроу-Хилл. стр.133–139. ISBN  0-07-035048-5.
2. Basavaraju, G; Гош, Дипин (1 февраля 1985 г.). Механика и термодинамика. Тата МакГроу-Хилл. С. 162–165. ISBN  978-0-07-451537-2.
3. Пластино, Ангел Р .; Муццио, Хуан К. (1992). «Об использовании и злоупотреблении вторым законом Ньютона для задач с переменной массой». Небесная механика и динамическая астрономия. Нидерланды: Kluwer Academic Publishers. 53 (3): 227–232. Bibcode:1992CeMDA..53..227P. Дои:10.1007 / BF00052611. ISSN  0923-2958. Получено 2011-12-30.
4. Бенсон, Том. «Уравнение идеальной ракеты». НАСА. Получено 30 декабря 2011.
5. Цветичанин, Л (1998-10-21). Динамика машин с переменной массой. (1-е изд.). CRC Press. С. 15–20. ISBN  978-90-5699-096-1.
6. Джанколи, Дуглас С. (2008). Физика для ученых и инженеров. 2 (4, иллюстрированное изд.). Pearson Education. С. 236–238. ISBN  978-0-13-227359-6.