Перестановка дерева - Tree rearrangement
Перестановки деревьев используются в эвристический алгоритмы посвященный поиску оптимальный древовидная структура. Их можно применять к любому набору данных, которые естественным образом организованы в дерево, но большинство приложений вычислительная филогенетика, особенно в максимальная экономия и максимальная вероятность поиски филогенетические деревья, которые стремятся идентифицировать одно из множества возможных деревьев, которое лучше всего объясняет эволюционный история конкретного ген или виды.
Основные перестановки деревьев

Ближайшая соседняя развязка (NNI)

Обрезка и пересадка поддерева (SPR)
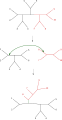
Деление дерева пополам и повторное соединение (TBR)
Простейшая перестановка дерева, известная как развязка ближайшего соседа, меняет возможность подключения четырех поддеревьев в основном дереве. Поскольку существует три возможных способа соединения четырех поддеревьев,[1] и один - исходное соединение, каждый обмен создает два новых дерева. Исчерпывающий поиск возможных ближайших соседей для каждого возможного набора поддеревьев - самый медленный, но наиболее оптимизирующий способ выполнения этого поиска. Альтернативный, более широкий поиск, обрезка и пересадка поддерева (SPR), выбирает и удаляет поддерево из основного дерева и повторно вставляет его в другое место в основном дереве, чтобы создать новый узел. В заключение, разделение дерева пополам и повторное соединение (TBR) отделяет поддерево от главного дерева во внутреннем узле, а затем пытается все возможные соединения между краями двух созданных таким образом деревьев. Возрастающая сложность техники перестановки дерева коррелирует с увеличением вычислительного времени, необходимого для поиска, хотя и не обязательно с их производительностью.[2]
SPR можно разделить на uSPR: Unrooted SPR, rSPR: Rooted SPR. uSPR применяется к некорневым деревьям и выглядит так: сломайте любой край. Присоедините один конец ребра (выбранный произвольно) к любому другому ребру в дереве. rSPR применяется к корневым деревьям * и идет: ломает любое ребро, кроме ребра, ведущего к корневому узлу. Соедините один конец ребра (а именно: край, который САМЫЙ ДАЛЬШЕ от корня) и прикрепите его к любому другому краю дерева.[3]
* В этом примере корень дерева отмечен узлом первой степени, что означает, что все узлы в дереве имеют степень 1 или степень 3. Альтернативный подход, используемый в Bordewich и Semple, заключается в рассмотрении корневого узла как иметь степень 2 и иметь специальное правило для rSPR.
Количество SPR[4] или TBR[5] ходы, необходимые для перехода от одного дерева к другому, могут быть рассчитаны путем создания леса максимального согласия, содержащего (соответственно) корневые или неукорененные деревья. Эта проблема является сложной NP, но с фиксированными параметрами.
Слияние деревьев
Самый простой тип слияния деревьев начинается с двух деревьев, которые уже определены как почти оптимальные; таким образом, они, скорее всего, имеют правильное большинство своих узлов, но могут не правильно разрешить отдельные «листья» дерева; например, разделение ((A, B), (C, D)) на конце ветви по сравнению с ((A, C), (B, D)) может быть неразрешенным.[1] Слияние деревьев меняет местами эти два решения между двумя деревьями, которые в остальном почти оптимальны. Варианты использования стандартного метода генетические алгоритмы с определенным целевая функция для замены поддеревьев с высокими показателями на основные деревья с высокими показателями в целом.[6]
Отраслевой поиск
Альтернативная стратегия - отсоединить часть дерева (которая может быть выбрана случайным образом или с использованием более стратегического подхода) и выполнить TBR / SPR / NNI для этого поддерева. Это оптимизированное поддерево затем можно заменить в основном дереве, что, надеюсь, повысит p-оценку.[7]
Дрейфующее дерево
Чтобы избежать попадания в ловушку локальных оптимумов, можно использовать подход «моделируемого отжига», при котором алгоритму иногда разрешается использовать неоптимальные деревья кандидатов с вероятностью, связанной с тем, насколько они далеки от оптимума.[7]
Сращивание деревьев
После того, как будет собран ряд одинаково оптимальных деревьев, часто можно найти лучшее дерево, комбинируя «хорошие части» отдельных деревьев. Подгруппы с идентичным составом, но разной топологией могут быть переключены, и полученные деревья оцениваются.[7]
использованная литература
- ^ а б Фельзенштейн Дж. (2004). Вывод филогении Sinauer Associates: Сандерленд, Массачусетс.
- ^ Такахаши К., Ней М. (2000). Эффективность быстрых алгоритмов филогенетического вывода по критериям максимальной экономии, минимальной эволюции и максимального правдоподобия при использовании большого количества последовательностей. Мол Биол Эвол 17(8):1251-8.
- ^ Bordewich M, Semple C. 2005. О вычислительной сложности отсечения корневого поддерева и расстояния повторного трансплантата Ann. Расческа. 8: 409–23
- ^ WHIDDEN, C., BEIKO, R.G. и ZEH, N. 2016. Фиксированные параметры и алгоритмы приближения для максимума Соглашение Леса разноцветных деревьев. Алгоритмика, 74, 1019–1054.
- ^ CHEN, J., FAN, J.-H. и SZE, S.-H. 2015. Параметризованные и аппроксимационные алгоритмы для леса максимального согласия в многофуркационных деревьях. Теоретическая информатика, 562, 496–512.
- ^ Мацуда Х. (1996). Филогенетический вывод белков с использованием максимального правдоподобия с помощью генетического алгоритма. Тихоокеанский симпозиум по биокомпьютингу 1996 г., pp512-23.
- ^ а б c Голобов, П. (1999). Анализ больших наборов данных в разумные сроки: решения для Composite Optima. Кладистика, 15 (4), 415–428. Дои:10.1006 / clad.1999.0122



