Предельная скорость - Terminal velocity

Для использования в других целях см. Конечная скорость (значения).

Сила тяжести, направленная вниз (F_грамм) равна сдерживающей силе сопротивления (F_d) плюс плавучесть. Чистая сила, действующая на объект, равна нулю, и в результате скорость объекта остается постоянной.

Предельная скорость - максимальная скорость, достижимая объектом при падении через жидкость (воздуха самый распространенный пример). Это происходит, когда сумма тащить сила (F_d) и плавучесть равна направленной вниз силе сила тяжести (F_грамм) действующий на объект. Поскольку равнодействующая сила на объекте ноль, у объекта ноль ускорение.^[1]

В динамика жидкостей, объект движется со своей конечной скоростью, если его скорость постоянна из-за сдерживающей силы, оказываемой жидкостью, в которой он движется ^[2].

По мере увеличения скорости объекта увеличивается и сила сопротивления, действующая на него, которая также зависит от вещества, через которое он проходит (например, воздуха или воды). На некоторой скорости сопротивление или сила сопротивления будут равны гравитационному притяжению объекта (плавучесть рассматривается ниже). В этот момент объект перестает ускоряться и продолжает падать с постоянной скоростью, называемой конечной скоростью (также называемой скоростью оседания). Объект, движущийся вниз со скоростью, превышающей предельную (например, потому что он был брошен вниз, упал из более тонкой части атмосферы или изменил форму), будет замедляться, пока не достигнет предельной скорости. Перетаскивание зависит от проектируемая площадь, здесь - сечение или силуэт объекта в горизонтальной плоскости. Объект с большой площадью проецирования относительно его массы, например парашют, имеет меньшую конечную скорость, чем объект с небольшой площадью проецирования относительно его массы, например дротик. В общем, для той же формы и материала конечная скорость объекта увеличивается с размером. Это связано с тем, что направленная вниз сила (вес) пропорциональна кубу линейного размера, но сопротивление воздуха приблизительно пропорционально площади поперечного сечения, которая увеличивается только как квадрат линейного размера. Для очень мелких объектов, таких как пыль и туман, предельная скорость легко преодолевается конвекционными потоками, которые не позволяют им достигать земли, и, следовательно, они остаются в воздухе в течение неопределенного времени. Загрязнение воздуха и туман являются примерами этого.

Примеры

График зависимости скорости парашютиста от времени, достигшего предельной скорости.

На основе сопротивления ветра, например, конечная скорость парашютист животом к земле (т.е. лицом вниз) свободное падение позиция около 195км / ч (120 миль / ч; 54 РС ).^[3] Эта скорость асимптотический предельное значение скорости, и силы, действующие на тело, уравновешивают друг друга все более и более по мере приближения к предельной скорости. В этом примере скорость 50% от скорости терминала достигается всего за 3 секунды, в то время как для достижения 90% требуется 8 секунд, для достижения 99% - 15 секунд и так далее.

Более высокие скорости могут быть достигнуты, если парашютист подтягивает свои конечности (см. Также свободно летающий ). В этом случае конечная скорость увеличивается примерно до 320 км / ч (200 миль / ч или 90 м / с),^[3] что почти конечная скорость сапсан ныряя на свою добычу.^[4] Такая же конечная скорость достигается для типичного .30-06 Пуля, падающая вниз - когда она возвращается на землю после выстрела вверх или падает с башни - согласно исследованию артиллерийского вооружения армии США 1920 года.^[5]

Конкуренция скоростные парашютисты лететь вниз головой и развивать скорость 530 км / ч (330 миль / ч; 150 м / с); текущий рекорд принадлежит Феликс Баумгартнер который прыгнул с высоты 128 100 футов (39 000 м) и достиг 1357,6 км / ч (840 миль / ч; 380 м / с), хотя он достиг этой скорости на большой высоте, где плотность воздуха намного ниже, чем у поверхности Земли. поэтому создает низкую силу сопротивления.

Биолог Дж. Б. С. Холдейн написал,

Для мыши и любого более мелкого животного [гравитация] практически не представляет опасности. Вы можете бросить мышь в шахту длиной в тысячу ярдов; и, достигнув дна, он получает легкий шок и уходит. Убита крыса, сломан человек, брызжет конь. Поскольку сопротивление воздуха движению пропорционально поверхности движущегося объекта.^[6]

Физика

Используя математические термины, терминальная скорость - без учета плавучесть эффекты - дается

${\displaystyle V_{t}={\sqrt {\frac {2mg}{\rho AC_{d}}}}}$

куда

• ${\displaystyle V_{t}}$ представляет конечную скорость,
• ${\displaystyle m}$ это масса падающего объекта,
• ${\displaystyle g}$ это ускорение силы тяжести,
• ${\displaystyle C_{d}}$ это коэффициент трения,
• ${\displaystyle \rho }$ это плотность жидкости, через которую падает объект, и
• ${\displaystyle A}$ это проектируемая площадь объекта.

В действительности объект приближается к своей предельной скорости асимптотически.

Эффекты плавучести из-за направленной вверх силы, действующей на объект окружающей жидкостью, можно учесть с помощью Принцип архимеда: масса ${\displaystyle m}$ должно быть уменьшено за счет вытесненной массы жидкости ${\displaystyle \rho V}$, с ${\displaystyle V}$ в объем объекта. Так что вместо ${\displaystyle m}$ использовать уменьшенную массу ${\displaystyle m_{r}=m-\rho V}$ в этой и последующих формулах.

Конечная скорость объекта изменяется из-за свойств жидкости, массы объекта и его проектируемого поперечного сечения. площадь поверхности.

Плотность воздуха увеличивается с уменьшением высоты примерно на 1% на 80 метров (260 футов) (см. барометрическая формула ). Для объектов, падающих через атмосферу, на каждые 160 метров (520 футов) падения конечная скорость уменьшается на 1%. После достижения местной конечной скорости, продолжая падение, скорость уменьшается для изменения скорости местного терминала.

Вывод для предельной скорости

Используя математические термины, определяя вниз как положительное, результирующая сила, действующая на объект, падающий у поверхности Земли, равна (согласно уравнение сопротивления ):

${\displaystyle F_{net}=ma=mg-{1 \over 2}\rho v^{2}AC_{d},}$

с v(т) скорость объекта как функция времени т.

В равновесие, то равнодействующая сила равно нулю (F_сеть = 0) и скорость становится конечной скоростью ^Lim
_т→∞ v(т) = V_т:

${\displaystyle mg-{1 \over 2}\rho V_{t}^{2}AC_{d}=0.}$

Решение для V_т дает

(5) ${\displaystyle V_{t}={\sqrt {\frac {2mg}{\rho AC_{d}}}}.}$

Вывод решения для скорости v как функция времени т

Уравнение сопротивления - предполагая ρ, грамм и Cd быть константами: ${\displaystyle ma=m{\frac {\mathrm {d} v}{\mathrm {d} t}}=mg-{\frac {1}{2}}\rho v^{2}AC_{d}.}$ Хотя это Уравнение Риккати которое может быть решено путем сведения к линейному дифференциальному уравнению второго порядка, проще отдельные переменные. Более практичный вид этого уравнения можно получить, сделав замену α^2 = ρACd/2мг. Разделив обе стороны на м дает ${\displaystyle {\frac {\mathrm {d} v}{\mathrm {d} t}}=g\left(1-\alpha ^{2}v^{2}\right).}$ Уравнение можно переформатировать в ${\displaystyle \mathrm {d} t={\frac {\mathrm {d} v}{g(1-\alpha ^{2}v^{2})}}.}$ Взяв интеграл от обеих частей, получаем ${\displaystyle \int _{0}^{t}{\mathrm {d} t^{\prime }}={1 \over g}\int _{0}^{v}{\frac {\mathrm {d} v^{\prime }}{1-\alpha ^{2}v^{\prime 2}}}.}$ После интеграции это становится ${\displaystyle t-0={1 \over g}\left[{\ln(1+\alpha v^{\prime }) \over 2\alpha }-{\frac {\ln(1-\alpha v^{\prime })}{2\alpha }}+C\right]_{v^{\prime }=0}^{v^{\prime }=v}={1 \over g}\left[{\ln {\frac {1+\alpha v^{\prime }}{1-\alpha v^{\prime }}} \over 2\alpha }+C\right]_{v^{\prime }=0}^{v^{\prime }=v}}$ или в более простой форме ${\displaystyle t={1 \over 2\alpha g}\ln {\frac {1+\alpha v}{1-\alpha v}}={\frac {\mathrm {arctanh} (\alpha v)}{\alpha g}},}$ с arctanh обратный гиперболический тангенс функция. В качестве альтернативы, ${\displaystyle {\frac {1}{\alpha }}\tanh(\alpha gt)=v,}$ с таном гиперболический тангенс функция. При условии, что грамм положительно (что и было определено), и подставив α назад, скорость v становится ${\displaystyle v={\sqrt {\frac {2mg}{\rho AC_{d}}}}\tanh \left(t{\sqrt {\frac {g\rho AC_{d}}{2m}}}\right).}$ Поскольку время стремится к бесконечности ( т → ∞), гиперболический тангенс стремится к 1, в результате чего конечная скорость ${\displaystyle V_{t}=\lim _{t\to \infty }v(t)={\sqrt {\frac {2mg}{\rho AC_{d}}}}.}$

Конечная скорость в ползущем потоке

Ползучий поток мимо сферы: рационализирует, сила сопротивления F_d и сила тяжести F_грамм

Для очень медленного движения жидкости силами инерции жидкости можно пренебречь (предположение о безмассовой жидкости) по сравнению с другими силами. Такие потоки называются ползучие потоки а условие, которое должно выполняться для того, чтобы потоки были ползущими, - это Число Рейнольдса, ${\displaystyle Re\ll 1}$. Уравнение движения для ползучего потока (упрощенное Уравнение Навье – Стокса ) дан кем-то

${\displaystyle {\mathbf {\nabla } }p=\mu \nabla ^{2}{\mathbf {v} }}$

куда

• ${\displaystyle {\mathbf {v} }}$ - векторное поле скорости жидкости,
• ${\displaystyle p}$ - поле давления жидкости,
• ${\displaystyle \mu }$ это жидкость флюид вязкость.

Аналитическое решение для ползучего обтекания шара было впервые дано Стокса в 1851 г. Из решения Стокса сила сопротивления, действующая на сферу, может быть получена как

${\displaystyle \quad (6)\qquad D=3\pi \mu dV\qquad \qquad {\text{or}}\qquad \qquad C_{d}={\frac {24}{Re}}}$

где число Рейнольдса, ${\displaystyle Re={\frac {1}{\mu }}\rho dV}$. Выражение для силы сопротивления, задаваемое уравнением (6), называется Закон Стокса.

Когда значение ${\displaystyle C_{d}}$ подставляется в уравнение (5), получаем выражение для предельной скорости сферического объекта, движущегося в условиях ползучего потока:

${\displaystyle V_{t}={\frac {gd^{2}}{18\mu }}\left(\rho _{s}-\rho \right),}$

куда ${\displaystyle \rho _{s}}$ это плотность объекта.

Приложения

Результаты ползучего потока могут быть применены для изучения оседания наносов у дна океана и падения капель влаги в атмосферу. Этот принцип также применяется в вискозиметр с падающей сферой, экспериментальное устройство, используемое для измерения вязкости высоковязких жидкостей, например нефти, парафина, гудрона и т. д.

Конечная скорость при наличии силы плавучести

Скорость оседания W_s песчинки (диаметр d, плотность 2650 кг / м³) в воде при 20 ° C, рассчитанный по формуле Soulsby (1997).

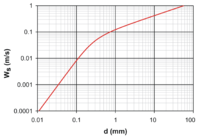
Если принять во внимание эффекты плавучести, объект, падающий через жидкость под собственным весом, может достичь предельной скорости (скорости оседания), если результирующая сила, действующая на объект, станет равной нулю. Когда достигается предельная скорость, вес объекта точно уравновешивается направленным вверх. сила плавучести и сила сопротивления. То есть

${\displaystyle \quad (1)\qquad W=F_{b}+D}$

куда

• ${\displaystyle W}$ = вес объекта,
• ${\displaystyle F_{b}}$ = сила плавучести, действующая на объект, и
• ${\displaystyle D}$ = сила сопротивления, действующая на объект.

Если падающий объект имеет сферическую форму, выражения для трех сил приведены ниже:

${\displaystyle {\begin{aligned}\quad &(2)\qquad &W&={\frac {\pi }{6}}d^{3}\rho _{s}g,\\\quad &(3)\qquad &F_{b}&={\frac {\pi }{6}}d^{3}\rho g,\\\quad &(4)\qquad &D&=C_{d}{\frac {1}{2}}\rho V^{2}A,\end{aligned}}}$

куда

• ${\displaystyle d}$ диаметр сферического объекта,
• ${\displaystyle g}$ - ускорение свободного падения,
• ${\displaystyle \rho }$ - плотность жидкости,
• ${\displaystyle \rho _{s}}$ - плотность объекта,
• ${\displaystyle A={\frac {1}{4}}\pi d^{2}}$ - площадь проекции сферы,
• ${\displaystyle C_{d}}$ - коэффициент лобового сопротивления, а
• ${\displaystyle V}$ - характерная скорость (принимаемая за конечную скорость, ${\displaystyle V_{t}}$).

Подстановка уравнений (2–4) в уравнение (1) и решение для конечной скорости, ${\displaystyle V_{t}}$ чтобы получить следующее выражение

${\displaystyle \quad (5)\qquad V_{t}={\sqrt {{\frac {4gd}{3C_{d}}}\left({\frac {\rho _{s}-\rho }{\rho }}\right)}}.}$

В уравнении (1) предполагается, что объект плотнее жидкости. В противном случае знак силы сопротивления следует сделать отрицательным, поскольку объект будет двигаться вверх против силы тяжести. Примерами являются пузырьки, образующиеся на дне бокала с шампанским и воздушные шары с гелием. Конечная скорость в таких случаях будет иметь отрицательное значение, соответствующее скорости подъема.

Смотрите также

• Закон Стокса
• Терминальная баллистика

Рекомендации

1. "Предельная скорость". НАСА Исследовательский центр Гленна. Получено 4 марта, 2009.
2. Riazi, A .; Тюркер, У. (январь 2019 г.). «Коэффициент сопротивления и скорость оседания частиц естественного осадка». Вычислительная механика частиц. Дои:10.1007 / s40571-019-00223-6.
3. Хуан, Цзянь (1999). "Скорость парашютиста (конечная скорость)". Книга фактов по физике. Гленн Элерт, средняя школа Мидвуд, Бруклинский колледж.
4. "Все о сапсане". Служба рыболовства и дикой природы США. 20 декабря 2007 г. Архивировано с оригинал 8 марта 2010 г.
5. Баллистик (март 2001 г.). "Пули в небе". W. Square Enterprises, 9826 Сагедейл, Хьюстон, Техас 77089. Архивировано из оригинал 31 марта 2008 г.
6. Холдейн, Дж. Б. С. (Март 1926 г.). "О том, чтобы быть правильным размером". Журнал Harper's. Архивировано из оригинал 2015-04-15. Альтернативный URL

внешняя ссылка

• Предельная скорость - сайт НАСА
• Бортовое видео о том, как твердотопливные ракетные ускорители космического корабля "Шаттл" быстро замедляются до предельной скорости при входе в более плотную атмосферу, от 2900 миль в час (3,8 Маха) в 5:15 на видео до 220 миль в час в 6:45, когда парашюты раскрываются через 90 секунд - видео и звук НАСА, @ io9.com.