Алгоритм Suurballes - Suurballes algorithm
В теоретическая информатика и сетевая маршрутизация, Алгоритм Суурбалле представляет собой алгоритм нахождения двух непересекающихся путей в неотрицательно взвешенном ориентированный граф, так что оба пути соединяют одну и ту же пару вершины и иметь минимальную общую длину.[1] Алгоритм был разработан Джоном В. Суурбаллом и опубликован в 1974 году.[2] Основная идея алгоритма Суурбалле заключается в использовании Алгоритм Дейкстры найти один путь, изменить веса ребер графа, а затем запустить алгоритм Дейкстры во второй раз. Выходные данные алгоритма формируются путем объединения этих двух путей, отбрасывания ребер, которые проходят пути в противоположных направлениях, и использования оставшихся ребер для формирования двух путей для возврата в качестве вывода. Модификация весов аналогична изменение веса в Алгоритм Джонсона, и сохраняет неотрицательность весов, позволяя второму экземпляру алгоритма Дейкстры найти правильный второй путь.
Задачу нахождения двух непересекающихся путей минимального веса можно рассматривать как частный случай минимальный расход проблема, где в данном случае есть две единицы «потока», а узлы имеют единицу «мощности». Алгоритм Суурбалле также можно рассматривать как частный случай алгоритма потока минимальной стоимости, который многократно проталкивает максимально возможный объем потока по кратчайшему пути увеличения. Первый путь, найденный алгоритмом Суурбалла, является кратчайшим путем увеличения для начального (нулевого ) потока, а второй путь, найденный алгоритмом Суурбалла, является кратчайшим дополняющим путем для остаточный график уходит после проталкивания одной единицы потока по первому пути.
Определения
Позволять грамм - взвешенный ориентированный граф с множеством вершин V и набор кромок E (рисунок А); позволять s обозначенная исходная вершина в грамм, и разреши т быть назначенной вершиной назначения. Пусть каждый край (ты,v) в E, из вершины ты к вершине v, имеют неотрицательную стоимость ш(ты,v).
Определять d (s,ты) быть ценой кратчайший путь к вершине ты из вершины s в дереве кратчайшего пути, уходящем корнями в s (рисунок C).
Примечание: узел и вершина часто используются как взаимозаменяемые.
Алгоритм
Алгоритм Суурбалле выполняет следующие шаги:
- Найдите дерево кратчайшего пути Т укорененный в узле s запуская алгоритм Дейкстры (рисунок C). Это дерево содержит для каждой вершины ты, кратчайший путь от s к ты. Позволять п1 быть кратчайшим путем затрат от s к т (рисунок B). Края в Т называются края деревьев а остальные ребра (края, отсутствующие на рисунке C) называются недеревянные ребра.
- Измените стоимость каждого ребра в графе, заменив стоимость ш(ты,v) каждого края (ты,v) к w ′(ты,v) = ш(ты,v) - d (s,v) + d (s,ты). В соответствии с полученной модифицированной функцией стоимости все ребра дерева имеют стоимость 0, а ребра, не являющиеся деревом, имеют неотрицательную стоимость. Например:
Если ты= B, v= E, тогда w ′(ты,v) = ш(B, E) - d (A, E) + d (A, B) = 2 - 3 + 1 = 0
Если ты= E, v= B, тогда w ′(ты,v) = ш(E, B) - d (A, B) + d (A, E) = 2 - 1 + 3 = 4 - Создать остаточный граф граммт сформированный из грамм удалив края грамм на пути п1 которые направлены в s а затем измените направление кромок нулевой длины вдоль пути п1 (рисунок D).
- Найдите кратчайший путь п2 в остаточном графе граммт запуская алгоритм Дейкстры (рисунок E).
- Удалите перевернутые края п2 с обоих путей. Остальные края п1 и п2 образуют подграф с двумя исходящими ребрами в s, два входящих ребра на т, и одно входящее и одно исходящее ребро в каждой оставшейся вершине. Следовательно, этот подграф состоит из двух рёберно непересекающихся путей из s к т и, возможно, некоторые дополнительные (нулевой длины) циклы. Верните два непересекающихся пути из подграфа.
Пример
В следующем примере показано, как алгоритм Суурбалля находит самую короткую пару непересекающихся путей из А к F.
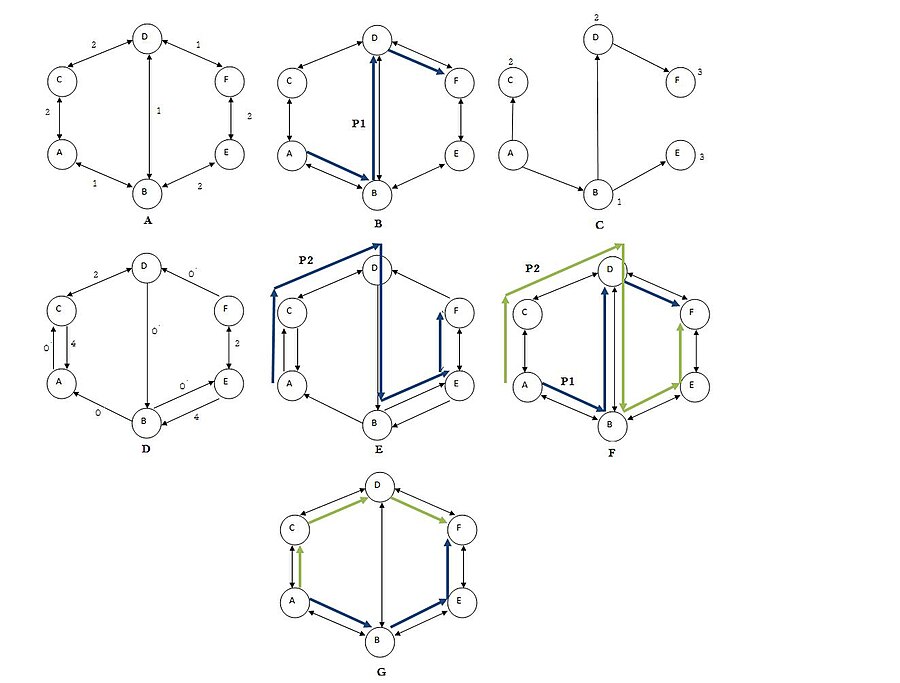
Фигура А иллюстрирует взвешенный график грамм.
Фигура B вычисляет кратчайший путь п1 из А к F (А–B–D–F).
Фигура C иллюстрирует дерево кратчайшего пути Т укорененный в А, а вычисленные расстояния от А в каждую вершину (ты).
Фигура D показывает остаточный график граммт с обновленной стоимостью каждого ребра и ребер пути 'P1 наоборот.
Фигура E вычисляет путь п2 в остаточном графе граммт (А–C–D–B–E–F).
Фигура F иллюстрирует оба пути п1 и путь п2.
Фигура грамм находит самую короткую пару непересекающихся путей путем объединения ребер путей п1 и п2 а затем отбрасывая общие перевернутые края между обоими путями (B–D). В результате получаем две кратчайшие пары непересекающихся путей (А–B–E–F) и (А–C–D–F).
Правильность
Вес любой дорожки из s к т в модифицированной системе весов равен весу в исходном графе, за вычетом d (s,т). Следовательно, два кратчайших непересекающихся пути с измененными весами являются теми же путями, что и два самых коротких пути в исходном графе, хотя они имеют разные веса.
Алгоритм Суурбалле можно рассматривать как частный случай метода последовательных кратчайших путей для поиска минимальный расход с общим объемом потока два из s к т. Изменение весов не влияет на последовательность путей, найденных этим методом, только на их веса. Следовательно, правильность алгоритма следует из правильности метода последовательных кратчайших путей.
Анализ и время работы
Этот алгоритм требует двух итераций алгоритма Дейкстры. С помощью Куча Фибоначчи, обе итерации могут быть выполнены за время куда и - количество вершин и ребер соответственно. Следовательно, такая же временная граница применяется к алгоритму Суурбалле.
Вариации
Версия алгоритма Суурбалла, описанная выше, находит пути, которые имеют непересекающиеся ребра, но могут иметь общие вершины. Можно использовать тот же алгоритм для поиска путей, не пересекающихся с вершинами, путем замены каждой вершины парой смежных вершин, одной со всеми входящими смежностями. u-in исходной вершины, и одна со всеми исходящими смежностями u-out. Два пути с непересекающимися ребрами в этом модифицированном графе обязательно соответствуют двум путям с непересекающимися вершинами в исходном графе, и наоборот, поэтому применение алгоритма Суурбалля к модифицированному графу приводит к построению двух вершинно-непересекающихся путей в исходном графе. Первоначальный алгоритм Суурбалле 1974 года был для вершинно-непересекающейся версии проблемы и был расширен в 1984 Суурбалле и Тарьяном до непересекающейся по ребрам версии.[3]
Используя модифицированную версию алгоритма Дейкстры, который одновременно вычисляет расстояния до каждой вершины т в графиках граммт, также можно найти суммарные длины кратчайших пар путей из заданной исходной вершины s ко всем остальным вершинам в графе за время, пропорциональное одному экземпляру алгоритма Дейкстры.
Примечание: пара смежных вершин, образовавшаяся в результате разделения, соединяется однонаправленным ребром с нулевой стоимостью от входящей к исходящей вершине. Исходная вершина становится s-out и конечная вершина становится банка.
Смотрите также
Рекомендации
- ^ Бхандари, Рамеш (1999), "Непересекающиеся парные алгоритмы Суурбалла", Живые сети: алгоритмы разнообразной маршрутизации, Springer-Verlag, стр. 86–91, ISBN 978-0-7923-8381-9.
- ^ Суурбалле, Дж. У. (1974), "Непересекающиеся пути в сети", Сети, 4 (2): 125–145, Дои:10.1002 / нетто.3230040204.
- ^ Suurballe, J. W .; Тарьян, Р.Э. (1984), «Быстрый метод поиска кратчайших пар непересекающихся путей» (PDF), Сети, 14 (2): 325–336, Дои:10.1002 / нетто.3230140209.



