Строительство Strähle - Strähle construction

Строительство Стрэле это геометрический метод определения длин для серии вибрирующие струны с одинаковыми диаметрами и натяжением на звук поля в конкретном рациональном закаленный музыкальный тюнинг. Впервые он был опубликован в 1743 г. Труды Шведская королевская академия наук шведского мастера орган производитель Даниэль Строле (1700–1746). Секретарь Академии Джейкоб Фагот приложил к статье неверно рассчитанный набор питчей, и эти цифры были воспроизведены Фридрих Вильгельм Марпург в Versuch über die musikalische Temperatur в 1776 году. В нескольких немецких учебниках, опубликованных около 1800 года, сообщалось, что ошибка была впервые обнаружена Кристлибом Бенедиктом Функом в 1779 году, но сама конструкция, похоже, не получала особого внимания до середины двадцатого века, когда теоретики настройки Дж. Мюррей Барбур представил это как хороший метод аппроксимации равный темперамент и аналогичные экспоненты малых корней и обобщили лежащие в основе математические принципы.
Он стал известен как устройство для создания резных музыкальных инструментов из статей математиков. Ян Стюарт и Исаак Якоб Шенберг Они хвалят его как уникальное и удивительно элегантное решение, разработанное неквалифицированным мастером.
Название «Strähle», используемое в недавних англоязычных работах, по-видимому, связано с ошибкой транскрипции в тексте Марпурга, где старомодный диакритический знак «е» был заменен выпуклым кольцом.[1]
Фон
Даниэль П. Строле работал строителем органов в центральной Швеции во второй четверти восемнадцатого века. Он работал подмастерьем у известного стокгольмского производителя органов Йохана Никласа Кахмана, а в 1741 году, через четыре года после смерти Кахмана, Строле получил привилегию заниматься изготовлением органов. Согласно системе, действовавшей в Швеции в то время, привилегия, предоставленная монополия, которой владели лишь некоторые из наиболее авторитетных производителей каждого типа музыкальных инструментов, давала ему законное право строить и ремонтировать органы, а также для обучения и проверки рабочих, а также служил гарантией качества работы и образования мастера.[2] Его орган 1743 года хранится в первоначальном состоянии в часовне на ул. Дворец Стремсхольм;[3] также известно, что он сделал клавикорды, и примечательный образец с необычной струнной шкалой и конструкцией, подписанной им и датированной 1738 годом, принадлежит Стокгольмский музей музыки.[4] Среди его учеников были его племянник Петтер Стрэле и Йонас Грен, партнеры в известных Стокгольмских органостроительных компаниях Gren & Stråhle,[5] и согласно Авраам Абрахамссон Хюльферс в его книге Historisk Afhandling om Musik och Instrumenter опубликованном в 1773 году, Строле сам изучал механику (которая, как предполагалось, включала математику[6]) с членом-учредителем Шведской академии наук Кристофер Польхем.[7] Он умер в 1746 году в Левстабруке на севере Уппланда.
Строле опубликовал свою конструкцию как «новое изобретение, чтобы определить Темперамент в настройке, для высоты звука клавикорда и подобных инструментов »в статье, появившейся в четвертом томе трудов только что образованной Шведской Королевской академии наук, которая включала статьи видных ученых и членов Академии Полхема, Карл Линней, Карл Фредрик Меннандер, Августин Эренсвярд, и Самуэль Клингеншерна. По словам органолога Евы Хелениус, музыкальный строй был предметом жарких споров в Академии в 1740-х годах.[8] и хотя сам Строле не был членом, это была третья статья на практические музыкальные темы, опубликованные Академией - первые две были написаны любителем музыкальных инструментов, министром и членом Академии Нильсом Брелином.[9] какие родственные изобретения применимы к клавесинам и клавикордам.[10]
Строле писал в своей статье, что он разработал этот метод «с некоторой мыслью и большим количеством попыток» с целью создания измерителя длины струн в темпераменте, который он описал как то, что вызывает темперирование («sväfningar ") самый мягкий для уха, а также наиболее удобный и равномерный набор звуков. Его инструкции производят нерегулярную настройку с диапазоном умеренных интервалов, подобную более известным настройкам, опубликованным в тот же период, но он не дал никаких дополнительных комментариев или описаний о самой настройке; сегодня это обычно считается приближением равный темперамент.[11] Он также не вдавался в подробности о каких-либо преимуществах своей конструкции, которая может давать точные и воспроизводимые результаты без вычислений или измерений только с помощью линейки и делителей; он описал конструкцию всего за пять шагов, и она менее итеративна, чем арифметические методы, описанные Dom Bédos de Celles метод определения длины органной трубы по интонации или Винченцо Галилей для определения положения струнных ладов примерно с одинаковым темпераментом, а также геометрические методы, такие как описанные Джозеффо Зарлино и Марин Мерсенн - все они известны гораздо лучше, чем у Строла. В заключение Строле заявил, что применил эту систему к клавикордам, хотя настройку, а также метод определения набора длин звучания можно использовать для многих других музыкальных инструментов, но мало доказательств того, что это было широко распространенная практика, кроме двух описанных в статье примеров, местонахождение которых сегодня неизвестно.
Строительство
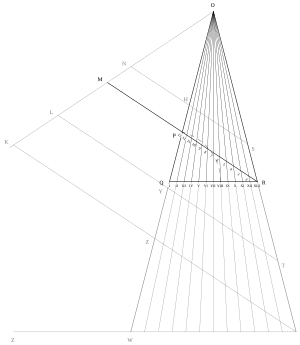
Сначала Строле велел нарисовать отрезок линии. QR удобной длины, разделенной на двенадцать равных частей, с точками, обозначенными I - XIII. QR затем используется как основание равнобедренного треугольника со сторонами OQ и ИЛИ ЖЕ вдвое дольше QR, и лучи, проведенные из вершины О через каждую пронумерованную точку на основании. Наконец, из вершины рисуется линия р под углом через точку п на противоположной стороне треугольника семь единиц от Q в точку M, расположенный вдвое дальше от р в качестве п. Длина МИСТЕР дает длину самого низкого звукового тона, а длину Депутат наибольшая из длин струн, генерируемых конструкцией, и длины звучания между ними определяются расстояниями от M к перекресткам МИСТЕР с линиями О я через O XIIв точках с 1 по 12.
Строле написал, что назвал линию PR «Linea Musica», который, как отметил Хелениус, был термином, который Польхем использовал в недатированной, но более ранней рукописи, теперь находящейся в Linköping Stiftsoch Landsbibliotek, и которая сопровождается записями композитора и геометра Харальда Валлериуса (1646–1716) и бывшего работодателя Строла. Дж. Н. Кахман.[8]
Строле также показал отрезки, параллельные МИСТЕР через точки NHS, LYT, и КЗВ чтобы проиллюстрировать, как однажды созданную конструкцию можно было масштабировать для приспособления к разным начальным шагам.
В заключение статьи Строле заявил, что он реализовал струнную гамму в трех высших октавах клавикорда, хотя неясно, была ли эта секция натянута на все той же проволокой одного калибра при одинаковом натяжении, как монохорд, который он написал. он был похож, и конструкция которого он описал более подробно. Он описал только косвенный метод настройки его настройки, однако, потребовав, чтобы он сначала установил эталонную высоту звука, передав соответствующие длины струн на подвижные перемычки на тринадцатиструнном монохорде с ключом, открытые струны которого ранее были настроены в унисон.а
Числовое представление Фэггота

Статья, следующая за Строле, была его математическим трактованием. Джейкоб Фагот (1699–1777), тогдашний секретарь Академии наук и будущий директор Геодезического бюро, который в том же томе также опубликовал статьи о мерах веса для щелока и методах расчета объема бочек. Фагот был одним из первых членов Академии, а также был членом специальной комиссии по мерам и весам.[12] Он, очевидно, не был музыкантом, хотя Хелениус описал, что интересовался музыкальными темами с математической точки зрения, и задокументировал, что он периодически контактировал с производителями музыкальных инструментов через Академию.[13] Хелениус также представил теорию о том, что Фагот оказал более активное, хотя и косвенное и посмертное влияние на создание музыкальных инструментов в Швеции, утверждая, что он, возможно, предложил длинные теноровые струны, используемые в двух экспериментальных инструментах, построенных Йоханом Броманом в 1756 году, которые она предложила. повлиял на тип клавикордов, построенных в Швеции в конце восемнадцатого и начале девятнадцатого веков.[14]
| Примечание | Педик | Stråhle[15] | |||
|---|---|---|---|---|---|
| Примечание | длина | центы | длина | центы | соотношение |
| C | 10000 | 0 | 10000 | 0 | 1/1 |
| c ♯ | 9379 | 111 | 9432 | 101 | 211/199 |
| d | 8811 | 219 | 8899 | 202 | 109/97 |
| d ♯ | 8290 | 325 | 8400 | 302 | 25/21 |
| е | 7809 | 428 | 7930 | 401 | 29/23 |
| ж | 7365 | 529 | 7490 | 500 | 239/179 |
| f ♯ | 6953 | 629 | 7073 | 600 | 41/29 |
| грамм | 6570 | 727 | 6676 | 699 | 253/169 |
| г ♯ | 6213 | 824 | 6308 | 798 | 65/41 |
| а | 5881 | 919 | 5955 | 897 | 89/53 |
| а ♯ | 5568 | 1014 | 5621 | 997 | 137/77 |
| б | 5274 | 1108 | 5303 | 1098 | 281/149 |
| c | 5000 | 1200 | 5000 | 1200 | 2/1 |
В своем анализе статьи Строла Фагот обрисовал в общих чертах тригонометрические шаги, которые он использовал для расчета длины звучания отдельных звуков, с целью сравнения новой настройки, созданной методом Строла, с настройкой с чистыми третями, четвертями и пятыми (помеченными как " N.1. "В таблице), и равный темперамент, который он назвал только" более старым темпераментом и [который] введен в Мистера Маттесона Critica Musica"(" N.2. "), Он намеревался получить результирующий набор цифр, чтобы показать," удовлетворяет ли настройка высоты звука в соответствии с ранее описанным изобретением слух приятными звуками и большей ровностью в Музыкальный высоты тона на клавишном инструменте, и поэтому учит пониманию лучше судить, чем старый и ранее известный способ настройки, когда глаз может видеть то, что слышит ухо ". б
Обе статьи были воспроизведены в немецком издании трудов Академии, опубликованном в 1751 г.[16] и таблица рассчитанных Фэгготом длин строк была впоследствии включена Марпург на его 1776 г. Versuch über die musikalische Temperatur,[1] который написал, что согласен с их точностью, но что вместо достижения заявленной цели "Strähle" настройка представляет собой неравный темперамент, "даже не терпимого типа".[1]
Длины звучания, рассчитанные Фаготом, существенно отличаются от тех, которые были бы получены в соответствии с инструкциями Строла, факт, который, по-видимому, был впервые опубликован Кристлиб Бенедикт Функ в Dissertatio de Sono et Tono в 1779 г.,[17] и созданная им настройка включает интервалы, настроенные за пределами диапазона, традиционно используемого в западной художественной музыке. Функу приписывают наблюдение этого несоответствия в Гелер с Physikalisches Wörterbuch в 1791 г.,[18] и Фишера Physikalisches Wörterbuch в 1804 г.,[19] и на ошибку указал Эрнст Хладни в Die Akustik в 1830 г.[20] Похоже, что за тот же период в Швеции не публиковалось подобных комментариев.
В этих работах сообщается об ошибке Фэггота в результате использования значения тангенса вместо столбца синуса из логарифмических таблиц. Сама ошибка заключалась в том, чтобы угол RP примерно на семь градусов больше, что привело к эффективной длине QP увеличить до 8,605. Это сильно преувеличило ошибки темперамента по сравнению с настройками, которые он представил вместе с ним, хотя неясно, наблюдал ли Фагот эти очевидные дефекты, поскольку он не делал дальнейших комментариев о конструкции или темпераменте Строла в статье.

Тюнинг
Настройка, произведенная в соответствии с инструкциями Строла, представляет собой рациональный темперамент с диапазоном квинт от 696 до 704 центов, что примерно на один цент ниже, чем у имел ввиду от пятого до двух центов только 3: 2; диапазон основных третей составляет от 396 до 404 центов, или десять центов ровно от 5/4 до трех центов. Пифагорейский 81/64. Эти интервалы попадают в пределы того, что считается приемлемым, но не существует распределения лучших третей по более часто используемым тональностям, которые характеризуют то, что сегодня является наиболее популярным строем, опубликованным в семнадцатом и восемнадцатом веках, которые известны как хорошие темпераменты. Лучшая квинта чиста в тональности F♯ или высоте тона, заданной МБ- у которого треть составляет 398 центов, а лучшая треть находится в тональности E, которая имеет пятую часть на 697 центов; лучшая комбинация двух интервалов находится в тональности F, а худшая комбинация - в тональности B.
Алгебраическое представление и геометрическое построение Барбура
Дж. Мюррей Барбур привлек новое внимание к конструкции Строла наряду с трактовкой ее Фэгготом в 20 веке. Представленный в контексте Марпурга, он включил его обзор наряду с более известными методами определения длины струны в свою книгу 1951 года. Тюнинг и темперамент где он охарактеризовал настройку как «приближение для равного темперамента». Он также продемонстрировал, насколько близка конструкция Строла к наилучшему приближению, которое может обеспечить метод, который снижает максимальные ошибки в основных третях и квинтах примерно на полцента и достигается заменой 7,028 длины QP.
Барбур представил более полный анализ конструкции в «Геометрическом приближении корней чисел», опубликованном шесть лет спустя в Американский математический ежемесячный журнал.[21] Он рассмотрел ошибку Фэггота и ее последствия, а затем вывел конструкцию Стрэля алгебраически, используя похожие треугольники. Это принимает обобщенный вид
Используя значения из инструкций Строла, это становится
Сдача так что приводит к форме первой формулы, которая более удобна для вычислений


Затем Барбур описал обобщенную конструкцию, используя легко получаемый средний пропорциональный на длину МБ это позволяет избежать большинства определенных углов и длин, которые требуются в оригинале. Для музыкальных приложений он проще и его результаты немного более однородны, чем у Строла, и он имеет то преимущество, что дает струны желаемой длины без дополнительного масштабирования.
Он приказал сначала провести линию МИСТЕР соответствует большему из двух чисел с Депутат меньшее, и построить их среднее, пропорциональное при МБ. Линия, которая будет нести деления, проводится от р под любым острым углом к МИСТЕР, а перпендикулярно ему проведена линия через B, который пересекает разделяемую линию в А, и РА распространяется на Q такой, что РА=AQ. Линия проводится из Q через п, пересекая линию через BA в О, и линия, проведенная из О к р. Строительство завершается разделением QR и рисовать лучи из О через каждое из подразделений.
В заключение Барбур обсудил характер и величину ошибок, возникающих при использовании обобщенной конструкции для аппроксимации экспонент различных корней, заявив, что его метод «прост и очень хорошо работает для малых чисел». Для корней от 1 до 2 ошибка составляет менее 0,13% - около 2 центов при N= 2 - с максимумом около м= 0,21 и м= 0,79. Кривая ошибки выглядит примерно синусоидальной, и для этого диапазона N можно приблизительно на 99% аппроксимировать путем аппроксимации кривой, полученной для N=1, . Ошибка быстро увеличивается для более крупных корней, для которых Барбур считал этот метод неприемлемым; кривая ошибок имеет вид с приближением максимума к м= 0 и м= 1 как N увеличивается.
Уточнения Шенбергом методов Барбура
Статья была опубликована с двумя примечаниями, добавленными ее рецензентом: Исаак Якоб Шенберг. Он заметил, что формула, полученная Барбуром, была дробно-линейным преобразованием и так называлась перспективностью, и что, поскольку три пары соответствующих точек на двух прямых однозначно определяют проективное соответствие, условие Барбура, что OA быть перпендикулярным QR не имеет значения. Отсутствие этого шага позволяет более удобно выбрать длину для QR, и сокращает количество операций.
Шенберг также отметил, что уравнение Барбура можно рассматривать как интерполяцию экспоненциальной кривой через три точки. м=0, м= 1/2 и м= 1, что он расширил в небольшой статье под названием «О расположении ладов на гитаре», опубликованной в Американский математический ежемесячный журнал в 1976 г.[22] Эта статья завершилась кратким обсуждением того, как Строле случайно использовал для полуоктавы, которая является одной из сходящихся непрерывное расширение фракции из , и его наилучшее рациональное приближение для размера знаменателя.
Стюарт и непрерывные дроби
Использование дробных приближений в конструкции Строле был расширен Яном Стюартом, который писал о конструкции в «Хорошо закаленном калькуляторе» в своей книге 1992 года. Еще одна точная математика, в которую вы меня втянули ... [23] а также "Беспокойное фиаско Фэггота", включенное в Музыка и математика опубликовано в 2006 году. Стюарт рассмотрел конструкцию с точки зрения проективной геометрии и вывел те же формулы, что и Барбур, рассматривая ее с самого начала как дробно-линейную функцию вида , и он указал, что приближение для неявно в конструкции , которая является следующей более низкой конвергенцией от получаемой ею половины октавы. Это следствие упрощения функции до за м= 0,5, где - порождающее приближение.
Аналогичные методы применимы к музыкальным инструментам.


Геометрические и арифметические методы разделения монохордов, а также грифы музыкальных инструментов, составленные Барбуром, были с заявленной целью иллюстрировать различные настройки, каждый из которых представляет или подразумевает, и работы Шенберга и Стюарта сохранили схожий фокус и ссылки. Три учебника по построению фортепиано, которые в них не включены, демонстрируют конструкции, аналогичные конструкциям Строла для создания новых инструментов, но независимо рассматривают настройку их высоты тона; обе конструкции используют неперпендикулярную форму, как это было предложено наблюдением Шенберга в работе Барбура «Геометрическое приближение к корням чисел», и одна дает оптимальные результаты, а другая демонстрирует приложение с корнем, отличным от 2.
Кютцинг
Карл Кютцинг, производитель органа и фортепиано из Берна в середине XIX века, написал в своей первой книге по дизайну фортепиано: Теоретико-практический Handbuch der Fortepiano-Baukunst с 1833 года, что он разработал простой метод определения длин звучания в октаве после прочтения различных геометрических конструкций, описанных в выпуске Марпурга. Historisch-kritischen Beitragen zur Aufnahme der Musik; он заявил, что деления будут очень точными и что конструкция может быть использована для изготовления гитар.
Кютцинг ввел конструкцию после описания большого сектор для той же цели. Он не включил ни один из методов в Das Wissenschaftliche der Fortepiano-Baukunst опубликована одиннадцатью годами позже, в которой он рассчитал длины, используя соотношение октавных длин приблизительно 18:35, и предложил новый метод с прерывистой кривой, скорректированной с учетом фактического диаметра проволоки, чтобы уменьшить тональные различия из-за скачков натяжения.[24]
Кютцинг получил указание расширить линейный сегмент до н.э- представляющий известную длину звучания - под углом 45 градусов к линии ba и от ее октавы в точке d расположен на полпути между б и c, чтобы продолжить линию, перпендикулярную ба пересекая это в е, затем разделить де на 12 равных частей. Смысл а на ab находится путем передачи длин де, db, из е далеко от б, а лучи выходили из а через точки, разделяющие де и пересекающиеся до н.э чтобы найти разные конечные точки длины строки из c.[25]
Такое расположение эквивалентно использованию среднего, пропорционального, для определения местоположения а.
Измененная схема с инструкциями была включена в брошюру, напечатанную крупнейшими производителями фортепиано в Англии. Джон Бродвуд и сыновья сопровождать их показ на 1862 Международная выставка в Лондоне, где они описали это как «практический метод определения длины струн для каждой ноты октавы при одинаковой темперации; так что с проволокой одного размера натяжение каждой ноты должно быть одинаковым».[26]
Он также был воспроизведен вместе с сектором Джакомо Сиверсом, русским мастером по изготовлению фортепиано, работающим в Неаполе, в его книге 1868 года. Il Pianoforte, где он утверждал, что это лучший практический метод определения длины звучания струн в фортепиано. Как и Бродвуд, Сиверс не описал его источник или степень его использования и не объяснил никакой теории, лежащей в основе этого. Он также не предполагал, что это могло быть использовано, кроме дизайна фортепиано.[27]
Wolfenden
Английский производитель фортепиано Сэмюэл Вольфенден представил конструкцию для определения всех длин струн, кроме самых низких по звучанию, в фортепиано. Трактат об искусстве конструирования фортепиано опубликовано в 1916 г .; как и Сиверс, он не объяснил, является ли это оригинальной процедурой или широко используемой, отметив лишь, что это «очень практичный метод определения длины строки, и в прошлые годы я использовал его полностью». Он добавил, что на момент написания статьи он обнаружил, что вычисление длины напрямую «несколько проще», и перед описанием поставил таблицу вычисленных длин для пяти верхних октав фортепиано.[28] Он включил частоты в одинаковой темперации, но опубликовал инструкции по настройке звука только в своем приложении 1927 года.
Вольфенден открыто выступал за выравнивание натяжения простых струн, которое он предлагал достичь в верхнем диапазоне, комбинируя соотношение 9:17 между длинами октав с равномерным изменением диаметров струн (достигая несколько более последовательных результатов по сравнению с аналогичной системой, опубликованной Зигфридом. Гансинг в 1888 году[29]), в отличие от шкалы Сиверса, чей график натяжения струн приводит к более высокому натяжению для более толстых и низких звуков.
Как и Сиверс, Вольфенден построил все длины зондирования на одном сегменте под углом 45 градусов от базовых линий для лучей, начиная с точек, расположенных для каждого C в диапазоне, рассчитанном на 54, 102, 192,5, 364 и 688 мм от верхней точки. . Затем четыре вершины для лучей располагаются на пересечениях горизонтальных базовых линий, продолжающихся от нижней C в каждой октаве, со второй линией, наклоненной под углом от верхней начальной точки для струнной линии, однако, как он указал, обе линии должны быть на уровне 51,5 градусов к базовым линиям и что базовые линии имеют соотношение 35:13 с разницей между двумя длинами октавы.
Метод Вольфендена приближает примерно с 1,3775, что эквивалентно в форме Барбура. Компенсация меньших октав дает 596 центов на половину октавы, ошибку около 1 мм на ноте F4 (f ') по сравнению с его расчетными значениями.
Примечания
- ^ а Строле (1743) стр. 285–286:
"Enligit detta påfund, har jag bygt et Монохордий, i så måtto, at det fullan hafver 13 strängar, ock skulle dy snarare heta Tredekachordium, мужчины som alla strängarna, äro af en номер, längd ock thon; så behåller jag det gamla namnet.
"Til dessa tretton strängar, är lämpadt et vanligit Руководство, афф эн Октава; мужчины под Hvar Sträng, седан де Noga äro stämde i унисон, sätter jag löfa stallar, å de пунктик, ок тилль де лангдер фра крепинерн, сом мин ну бескрефне Linea Musica Det äfkar: derefter hvar sträng undfår sin behöriga thon.
"Дет Claver, som jag här til förfärdigat är jämnväl i de tre högre Octaverne, noga rättadt efter мин Linea Musica, til strängarnes längd ock skilnad: ock på det stämningen, må utan besvär, kunna ske; så är mit Монохордий så giordt, at det kan ställas ofvan på Claveret, då en Октав på Claveret stämmes, thon för thon, mot sina tillhöriga thoner på Монохордий, derefter alla de andra thonerne, å Claveret, stämmas Октавы-vis; den stamningen, är ock för örat lättast at värkställa, emedan den bör vara fri för svängningar ».
- ^ б Пидор (1743) стр. 286:
"Huruvida thonernes stämning, efter förut beskrefne Påfund, förnöger hörsten, medbegeligare ljud, ock med bättre likstämmighet, i de Musikaliska thonerne å et Claver, ан де гамла ок хартилс беканта стэмнингс сатт, дером лерер фёрстондет баттре кунна дама, нар ёгат фар се дет ёрат хёрер ».
- ^ Марпург (1776 г.) стр. 167–168:
"Ich muss gestehen, dass sich dieser Aufsatz mit Vergnügen lesen lässet, und dass ich von der Richtigkeit der vom Hrn. Jacob Fagot, durch eine sehr mühsame trigonometrische Berechnung der Strählischen Liniennüberzeünden, gefunden der hhlischen Züberzügen, gefunden. gefunden Zahlen nicht geben, was sie geben sollen, und was Hr. Strähle suchte, nemlich eine Temperatur, welche das Schweben am gelindesten für das Gehör macht, und alle Töne in gehörige Gleichstimmigkeitsweemente néeperaté nénée néréné néréné. und nicht einmal von der erträglichsten Art. "
Рекомендации

- Daniel P. Stråhle "Nytt Påfund", Финляндия Температураn i stämningen, för thonerne å Claveret ock dylika Instrumenter " Kongliga Swenska Wetenskaps Academiens Handlingar för Månaderne октябрь, ноябрь, ок. декабрь, т. IV, Лоренц Людвиг Грефинг, Стокгольм, 1743 стр. 281–285
- Джейкоб Фагот "Trigonometrisk uträkning på en ny Температур, för thonernes stämning å Claveret " Kongliga Swenska Wetenskaps Academiens Handlingar för Månaderne Октябрь, ноябрь, октябрь, т. IV, Лоренц Людвиг Грефинг, Стокгольм, 1743 стр. 286-291
- Ян Стюарт «Беспокойное фиаско Пидора» Джон Фовел, Раймонд Флуд, Робин Уилсон, изд. Музыка и математика Oxford University Press, 2006 г., стр. 68-75
- Дж. Мюррей Барбур Тюнинг и темперамент: исторический обзор Michigan State College College Press, East Lansing 1951 p. 65–68
- ^ а б Вильгельм Фридрих Марпург Versuch über die musikalische Temperatur 1776 с.167-168
- ^ Ева Хелениус-Оберг "Свенское инструментальное производство 1720-1800 - En Preliminär Översikt" Svensk Tidskrift for Musikforskning, 1977 стр.22
- ^ История: дворец Стремсхольм Королевские дворцы - Королевский двор (по состоянию на 14 октября 2009 г.)
- ^ Эдвард Л. Коттик и Джордж Лактенберг, Ранние клавишные инструменты в европейских музеях Издательство Индианского университета 1997, стр.196
Даниэль Строле, 1738 г. Клавикорд, инв. номер N145765 - Stockholm Music Museum (по состоянию на 28 августа 2009 г.) - ^ "Йонас Грен" Nordisk Familjebok femte band, Gernandts boktryckeri-aktiebolag, Стокгольм. 1882 с.1554
- ^ Керала Дж. Снайдер Орган как зеркало своего времени: размышления Северной Европы, 1600-2000 гг. Oxford University Press, 2002, стр.8, 15
- ^ Тобиас Норлинд Свенск Музыкальная история Helsingborgs Typografiska Anstalt, Helsingborg 1901. p. 132
- ^ а б Ева Хелениус-Оберг "Cembalon i Sverige samt Frågan om det Svenska Klavikordets Uppkomst" Svensk Tidskrift for Musikforskning 1979 с.31-42
- ^ "Нильс Брелин" Nordisk Familjebok fjärde bandet Nordisk Familjeboks förlags aktiebolag Stockholm 1905 стр.86
- ^ Нильс Брелин "Et Påfund at Storligen öka" Клавиры ох Цимбалеры Годхет " Kongliga Swenska Wetenskaps Academiens Handlingar, för Månaderne Julius, август и сентябрь 1739 г., т. 1, стр.81; Nils Brelin "Beskrifning öfver det nyt Påfund af en uprät-stående dubbel Clavesin, inrättad met forte och Piano до 8-ми классников в возрасте 1741 года. Риксдаг для Riksens Högloflf. Изобрет. Kongliga Swenska Wetenskaps Academiens Handlingar, för Månaderne Julius, август и сентябрь, том 3, с.218
- ^ Барбур (1951) стр.65.
- ^ "Якоб Фагот" Nordisk Familjebok Band 7, Nordisk familjeboks förlags aktiebolag, Стокгольм 1907, стр.1259
- ^ Ева Хелениус-Оберг "Kyrkoherden Nils Brelin — Mechanicus och Klaverälskare" Svensk Tidskrift for Musikforskning 1987 с.112
- ^ Инструменты - клавесин и клавикорд, оба из коллекции Стокгольмского музыкального музея - отличаются чрезвычайно большим размером и длинными тенорными струнами, где удвоение длины струны простирается на пять октав, три октавы и четверть соответственно. Оба включают в себя многие идеи, описанные Брелином в статье «Труды Академии 1739 года»; Гелениус (1979)
Иоганнес Броман, клавесин, Стокгольм 1756 г. Музей № 83118 Стокгольмский музыкальный музей; Иоганнес Броман, клавикорд, Стокгольм 1756 г. Музей № N57244 Stockholm Music Museum (доступ 13 сентября 2009 г.) - ^ Барбур (1951) стр.68.
- ^ Дэн. P. Stråhle, Neue Erfindung die Temperatur beym Stimmen für Töne auf dem Clavier u. d. грамм. Instrumenten zu finden. Якоб Фагот, Trigonometrische Berechnung für die neue Temperatur zu Stimmung der Töne auf dem Claviere. Der Königl. Schwedischen Akademie der Wissenschaften. Abhandungen, aus der Naturlehre, Haushaltungskunst und Mechanik, auf das Jahre 1743. fünfter Band. aus dem Schwedischen übersetzt, von Abraham Gotthelf Kästner. Георг Кристиан Грунд, Гамбург; Адам Генрих Холле, Лейпциг 1751 стр. 226-229, 230-234
- ^ рассмотрено в «Лейпциге» Göttingische Anzeigen von gelehrten Sachen unter der Aufsicht der Königl. Gesellschaft der Wissenschaften. 32 Stück (11 марта 1780 г.) Erste Band. Иоганн Христиан Дитрих, Геттинген, 1780 г.
В статье сообщалось, что в самой настройке нет ничего нового, поскольку она не сильно отличается от обычного деления октавы. - ^ Dissertatio de Sono et Tono. Лейпциг. 1779,4; цитируется Иоганном Самуэлем Трауготтом Гелером "Тон" Physikalisches Wörterbuch oder Versuch einer Erklärung der vornehmsten Begriffe und Kunstwörter der Naturlehre Vierter Theil. Schwickertschen Verlage, Лейпциг 1791, стр.387-388
- ^ Иоганн Карл Фишер "Тон" Physikalisches Wörterbuch oder Erklärung der vornehmsten zur Physik Fünfter Theil. Генрих Дитрих, Геттинген 1804 г. стр.26
- ^ Эрнест Флоренс Фридрих Хладни Die Akustik Breitkopf & Härtel, Лейпциг 1830 г. стр.39
- ^ Дж. Мюррей Барбур "Геометрическое приближение корней чисел" Американский математический ежемесячный журнал т. 64 (1957) с. 1-9
- ^ Исаак Дж. Шенберг "О расположении ладов на гитаре" Американский математический ежемесячный журнал т. 83, 1976, с.550-2.
- ^ Ян Стюарт Еще одна точная математика, в которую вы меня втянули ... Courier Dover Publications, 2004, стр.246-252
- ^ Карл Кютцинг. Das Wissenschaftliche der Fortepiano-Baukunst. J. F. J. Dalp. Берн и Кур, 1844 г.
- ^ Карл Кютцинг. Теоретико-практический Handbuch der Fortepiano-Baukunst. J. F. J. Dalp. Bern und Chur, 1833. С. 20-21.
- ^ Аластер Лоуренс. Эволюция рояля Бродвуд 1785-1998 гг. "Рис. 6/6: Геометрия шкалы Бродвуда, 1862 г." Музыкальный факультет Йоркского университета, сентябрь 1998 г., стр.151
- ^ Джакомо Сиверс, Il Diagramma per lo spartimento delle corde. Il pianoforte; Guida Pratica per Costruttori, Accordatori, Dilettanti e Possessori di Pianoforti Stabilimento Tipografico Ghio, Napoli 1868. p.103-104.
- ^ Самуэль Вулфенден, Длина и диаметр струн. Трактат об искусстве конструирования фортепиано 1916, перепечатано Unwin Brothers, Лондон, 1975, стр. 23-33.
- ^ Зигфрид Хансинг Фортепиано и его акустические свойства второе издание в переводе Эмми Хансинг-Перзина. Зигфрид Хансинг, Шверин i. М., 1904 с.84















