Солитонная модель в нейробиологии - Soliton model in neuroscience

Измерение нелинейной электромеханической волны в искусственной липидной системе

В солитонная гипотеза в нейробиология это модель Это утверждает, что объясняет, как потенциалы действия инициируются и проводятся вместе аксоны основан на термодинамической теории распространения нервных импульсов.^[1] Он предполагает, что сигналы проходят по клеточному мембрана в виде определенных видов уединенный звук (или же плотность ) импульсы, которые можно смоделировать как солитоны. Модель предлагается в качестве альтернативы модели Модель Ходжкина – Хаксли^[2] в котором потенциалы действия: потенциалзависимые ионные каналы в мембране открыть и позволить натрию ионы войти в ячейку (входящий ток). Результирующее снижение мембранного потенциала открывает близлежащие потенциалозависимые натриевые каналы, тем самым распространяя потенциал действия. Трансмембранный потенциал восстанавливается за счет задержки открытия калиевых каналов. Сторонники солитонной гипотезы утверждают, что энергия в основном сохраняется во время распространения, за исключением потерь на диссипацию; Измеренные изменения температуры полностью не согласуются с моделью Ходжкина-Хаксли.^[3][4]

Солитонная модель (и звук волн в целом) зависит от адиабатического распространения, при котором энергия, выделяемая в источнике возбуждения, адиабатически переносится через среду, то есть плазматическую мембрану. Измерение температурного импульса и заявленное отсутствие тепловыделения при потенциале действия^[5][6] были основой предположения, что нервные импульсы - это адиабатическое явление, во многом напоминающее звуковые волны. Синаптически вызванные потенциалы действия в электрическом органе электрического угря связаны со значительным (только) положительным выделением тепла с последующим активным охлаждением до температуры окружающей среды.^[7] В обонятельном нерве саргана потенциал действия связан с двухфазным изменением температуры; тем не менее, есть чистое производство тепла.^[8] Эти опубликованные результаты несовместимы с моделью Ходжкина-Хаксли, и авторы интерпретируют свою работу в терминах этой модели: начальный натриевый ток выделяет тепло по мере разряда мембранной емкости; тепло поглощается во время перезарядки емкости мембраны, поскольку ионы калия движутся с градиентом их концентрации, но против потенциала мембраны. Этот механизм называется «Теорией конденсатора». Дополнительное тепло может генерироваться изменениями конфигурации мембраны, вызванными изменениями мембранного потенциала. Увеличение энтропии во время деполяризации приведет к выделению тепла; увеличение энтропии во время реполяризации поглотит тепло. Однако любые такие энтропийные вклады несовместимы с моделью Ходжкина и Хаксли.^[9]

История

Ичидзи Тасаки впервые применил термодинамический подход к феномену распространения нервных импульсов, который выявил несколько явлений, которые не были включены в Модель Ходжкина – Хаксли.^[10] Наряду с измерением различных неэлектрических компонентов нервного импульса Тасаки исследовал физическую химию фазовые переходы в нервных волокнах и его важность для распространения нервного импульса. Основываясь на работе Тасаки, Конрад Кауфман предложил звуковые волны в качестве физической основы для распространения нервных импульсов в неопубликованной рукописи.^[11] Основная идея, лежащая в основе солитонной модели, заключается в уравновешивании внутренней дисперсии двумерных звуковых волн в мембране за счет нелинейных упругих свойств вблизи фазового перехода. Начальный импульс в таких условиях может приобретать устойчивую форму, известную как уединенная волна.^[12] Солитоны представляют собой простейшее решение системы нелинейных волновых уравнений, описывающих такое явление, и были применены для моделирования нервного импульса в 2005 году Томасом Хаймбургом и Эндрю Д. Джексоном,^[13][14][15] как в Институт Нильса Бора из Копенгагенский университет. Хаймбург возглавляет группу мембранной биофизики института. Группа биологической физики Маттиаса Шнайдера изучила распространение двумерных звуковых волн в липидных поверхностях и их возможную роль в биологической передаче сигналов. ^{[16][17][18][19]}

Обоснование

Модель начинается с наблюдения, что клеточные мембраны всегда имеют Точка замерзания (температура, ниже которой консистенция меняется с жидкой на гелеобразную) лишь немного ниже температуры тела организма, и это позволяет распространяться солитонам. Потенциал действия, перемещающийся по смешанному нерву, приводит к небольшому повышению температуры, за которой следует ее понижение.^[20] Сторонники солитонной модели утверждают, что в течение всего импульса не выделяется чистое тепло, и что наблюдаемые изменения температуры несовместимы с моделью Ходжкина-Хаксли. Однако это неверно: модель Ходжкина-Хаксли предсказывает двухфазное выделение и поглощение тепла.^[9] Кроме того, потенциал действия вызывает небольшое локальное утолщение мембраны и силу, действующую наружу;^[21] этот эффект не предсказывается моделью Ходжкина – Хаксли, но и не противоречит ей.

Модель солитона пытается объяснить электрические токи, связанные с потенциалом действия, следующим образом: бегущий солитон локально изменяет плотность и толщину мембраны, а поскольку мембрана содержит много заряженных и полярный веществ, это приведет к электрическому эффекту, подобному пьезоэлектричество. Действительно, теперь было показано, что такие нелинейные звуковые волны существуют на липидных поверхностях раздела, которые показывают внешнее сходство с потенциалами действия (электрооптомеханическое взаимодействие, скорости, форма двухфазного импульса, порог возбуждения и т. Д.).^[17] Кроме того, волны остаются локализованными в мембране и не распространяются в окружающей среде из-за несоответствия импеданса.^[22]

Формализм

Солитон, представляющий потенциал действия нервов, является решением уравнение в частных производных

${\displaystyle {\frac {\partial ^{2}\Delta \rho }{\partial t^{2}}}={\frac {\partial }{\partial x}}\left[\left(c_{0}^{2}+p\Delta \rho +q\Delta \rho ^{2}\right){\frac {\partial \Delta \rho }{\partial x}}\right]-h{\frac {\partial ^{4}\Delta \rho }{\partial x^{4}}},}$

куда т время и Икс положение вдоль аксона нерва. Δρ - изменение плотности мембраны под действием потенциала действия, c₀ - скорость звука нервной оболочки, п и q описывают характер фазового перехода и тем самым нелинейность упругих постоянных нервной мембраны. Параметры c₀, п и q продиктованы термодинамическими свойствами нервной мембраны и не могут регулироваться свободно. Их нужно определять экспериментально. Параметр час описывает частотную зависимость скорости звука мембраны (соотношение дисперсии ). Приведенное выше уравнение не содержит никаких подгоночных параметров. Формально он относится к Приближение Буссинеска для солитонов в водных каналах. Решения приведенного выше уравнения обладают предельной максимальной амплитудой и минимальной скоростью распространения, которые аналогичны скорости импульса в миелинизированных нервах. При ограничительных предположениях существуют периодические решения, отображающие гиперполяризационные и рефрактерные периоды.^[23]

Роль ионных каналов

Сторонники солитонной модели утверждают, что она объясняет несколько аспектов потенциала действия, которые не объясняются моделью Ходжкина – Хаксли. Поскольку он имеет термодинамическую природу, он не касается свойств отдельных макромолекул, таких как ионный канал белки в молекулярном масштабе. Скорее предполагается, что их свойства неявно содержатся в макроскопических термодинамических свойствах нервных мембран. Солитонная модель предсказывает флуктуации мембранного тока во время действия потенциала действия. Эти токи похожи на те, что описаны для белков ионных каналов.^[24] Считается, что они вызваны порами липидной мембраны, спонтанно возникающими в результате тепловых колебаний. Такие тепловые флуктуации объясняют специфическую ионную селективность или конкретный временной ход реакции на изменения напряжения на основе их влияния на макроскопическую восприимчивость системы.

Применение к анестезии

Авторы утверждают, что их модель объясняет ранее неясный способ действия многочисленных анестетики. В Наблюдение Мейера – Овертона считает, что сила широкого спектра химически разнообразных анестетиков пропорциональна их липид растворимость, предполагая, что они не действуют путем связывания со специфическими белки например, ионные каналы, но вместо этого растворяясь в липидной мембране и изменяя ее свойства. Растворение веществ в мембране понижает точку замерзания мембраны, и в результате большая разница между температурой тела и точкой замерзания препятствует распространению солитонов.^[25] Увеличивая давление, снижая pH или понижая температуру, эту разницу можно восстановить до нормы, что должно отменить действие анестетиков: это действительно наблюдается. Величина давления, необходимая для отмены действия анестетика с данной растворимостью в липидах, может быть вычислена из солитонной модели и достаточно хорошо согласуется с экспериментальными наблюдениями.

Различия между модельными предсказаниями и экспериментальными наблюдениями

Столкновение солитонов

Ниже приводится список некоторых разногласий между экспериментальными наблюдениями и «солитонной моделью»:

Антидромное вторжение в сому из аксона

Потенциал действия, инициированный в любом месте аксона, будет перемещаться в антидромном (обратном) направлении к соме нейрона (телу клетки) без потери амплитуды и произведет в соме потенциал действия полной амплитуды. Поскольку площадь мембраны сомы на несколько порядков больше площади аксона, сохранение энергии требует уменьшения амплитуды адиабатической механической волны. Поскольку отсутствие тепловыделения является одним из заявленных оправданий «солитонной модели», это особенно трудно объяснить в рамках этой модели.^{[26][нужна цитата ]}

Сохранение потенциала действия в широком диапазоне температур

Важным предположением солитонной модели является наличие фазового перехода вблизи температуры окружающей среды аксона (см. «Формализм» выше). Тогда быстрое изменение температуры от температуры фазового перехода обязательно вызовет большие изменения в потенциале действия. Ниже температуры фазового перехода возникновение солитонной волны невозможно. Тем не менее, потенциалы действия присутствуют при 0 ° C. Ход во времени замедляется способом, предсказываемым измеренной кинетикой открытия и закрытия ионных каналов Ходжкина-Хаксли.^[27]

Столкновения

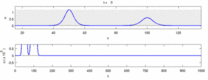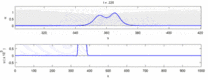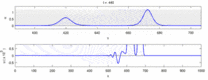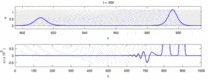
Нервные импульсы, идущие в противоположных направлениях, при столкновении уничтожают друг друга.^[28] С другой стороны, механические волны не аннигилируют, а проходят друг через друга. Сторонники солитонной модели пытались показать, что потенциалы действия могут проходить через столкновение;^[29] однако, столкновение аннигиляции ортодромных и антидромный потенциалы действия - это обычное явление, наблюдаемое в лабораториях нейробиологии, и основа стандартной техники идентификации нейронов.^[30] Солитоны пересекают друг друга при столкновении (рисунок - «Столкновение солитонов»), уединенные волны в целом могут проходить, аннигилировать или отскакивать друг от друга.^[31] а солитоны - лишь частный случай таких уединенных волн.^[32]

Ионные токи под напряжением фиксатора

Зажим напряжения, использованный Ходжкином и Хаксли (1952) (Модель Ходжкина-Хаксли ), чтобы экспериментально проанализировать потенциал действия в аксоне гигантского кальмара, использует электронную обратную связь для измерения тока, необходимого для поддержания постоянного напряжения на мембране на заданном уровне. Серебряная проволока, вставленная внутрь аксона, создает постоянное мембранное напряжение по длине аксона. В этих условиях нет возможности бегущего «солитона». Любые термодинамические изменения сильно отличаются от изменений, вызванных потенциалом действия. Тем не менее, измеренные токи точно воспроизводят потенциал действия.^{[нужна цитата ]}

Одноканальные токи

Метод патч-зажима изолирует микроскопический участок мембраны на кончике стеклянной пипетки. Затем можно регистрировать токи от одиночных ионных каналов. Нет возможности распространения солитонов или термодинамических изменений. Тем не менее, свойства этих каналов (временная реакция на скачки напряжения, ионная селективность) точно предсказывают свойства макроскопических токов, измеренных с помощью обычных фиксаторов напряжения.^[33]

Селективная ионная проводимость

Ток, лежащий в основе деполяризации потенциала действия, селективен для натрия. Реполяризация зависит от селективного калиевого тока. Эти токи имеют очень специфические реакции на изменения напряжения, которые количественно объясняют потенциал действия. Замена натрия непроницаемыми ионами устраняет потенциал действия. «Солитонная модель» не может объяснить ни ионную селективность, ни реакцию на изменение напряжения.

Фармакология

Препарат тетродотоксин (ТТХ) блокирует потенциалы действия при чрезвычайно низких концентрациях. Место действия ТТХ на натриевые каналы не установлено.^[34] Дендротоксины блокируют калиевые каналы. Эти препараты вызывают количественно предсказуемые изменения потенциала действия.^[33] «Солитонная модель» не дает объяснения этим фармакологическим эффектам.

Волны действий

Недавняя теоретическая модель, предложенная Ахмедом Эль Хади и Бенджамином Махта, предполагает, что существует механическая поверхностная волна, которая распространяется вместе с электрическим потенциалом действия. Эти поверхностные волны называются «волнами действия».^[35] В модели Эль-Хади-Махта эти совместно распространяющиеся волны вызываются изменениями напряжения на мембране, вызванными потенциалом действия.

Смотрите также

• Биологические модели нейронов
• Модель Ходжкина – Хаксли
• Векторный солитон

Источники

• Федерико Фарачи (2013) "60-летие модели Ходжкина-Хаксли: критическая оценка с исторической точки зрения и точки зрения моделистов "
• Ревати Аппали, Урсула ван Ринен, Томас Хаймбург (2012) "Сравнение модели Ходжкина-Хаксли и теории солитонов для потенциала действия на нервы "
• Волны действия в мозгу, The Guardian, 1 мая 2015 г.
• Ичидзи Тасаки (1982) "Физиология и электрохимия нервных волокон "
• Конрад Кауфман (1989) "Потенциалы действия и электрохимическая связь в макроскопической хиральной фосфолипидной мембране ".
• Андерсен, Джексон и Хаймбург "К термодинамической теории распространения нервных импульсов "
• Прадип Дас; W.H. Шварц (4 ноября 1994 г.). «Солитоны в клеточной мембране». Физический обзор E. 51 (4): 3588–3612. Bibcode:1995PhRvE..51.3588D. Дои:10.1103 / PhysRevE.51.3588. PMID  9963042.
• Возвращаясь к механике потенциала действия, Princeton University Journal watch, 1 апреля 2015 г.
• На (звуковой) дорожке анестетиков, Eurekalert, согласно пресс-релизу Копенгагенского университета от 6 марта 2007 г.
• Kaare Grsbøll (2006). «Функция нервов - действие анестетиков» (PDF). Гамма. 143. Элементарное введение.
• Уединенные акустические волны распространяются на границе раздела липидной мембраны, Phys.org 20 июня 2014 г.

Рекомендации

1. Андерсен, S; Джексон, А; Хаймбург, Т. (2009). «К термодинамической теории распространения нервных импульсов» (PDF). Прогресс в нейробиологии. 88 (2): 104–113. Дои:10.1016 / j.pneurobio.2009.03.002. PMID  19482227.
2. Ходжкин А.Л., Хаксли А.Ф., Кац Б (1952). «Токи, переносимые ионами натрия и калия через мембрану гигантского аксона Лолиго». Журнал физиологии. 116 (4): 424–448. Дои:10.1113 / jphysiol.1952.sp004717. ЧВК  1392213. PMID  14946713.
   Ходжкин А.Л., Хаксли А.Ф. (1952). «Токи, переносимые ионами натрия и калия через мембрану гигантского аксона Лолиго». Журнал физиологии. 116 (4): 449–472. Дои:10.1113 / jphysiol.1952.sp004717. ЧВК  1392213. PMID  14946713.
   Ходжкин А.Л., Хаксли А.Ф. (1952). «Компоненты проводимости мембраны в гигантском аксоне Лолиго». J Physiol. 116 (4): 473–496. Дои:10.1113 / jphysiol.1952.sp004718. ЧВК  1392209. PMID  14946714.
   Ходжкин А.Л., Хаксли А.Ф. (1952). «Двойное влияние мембранного потенциала на проводимость натрия в гигантском аксоне Лолиго». J Physiol. 116 (4): 497–506. Дои:10.1113 / jphysiol.1952.sp004719. ЧВК  1392212. PMID  14946715.
   Ходжкин А.Л., Хаксли А.Ф. (1952). «Количественное описание мембранного тока и его применение к проводимости и возбуждению в нерве». J Physiol. 117 (4): 500–544. Дои:10.1113 / jphysiol.1952.sp004764. ЧВК  1392413. PMID  12991237.
3. Марджиняну, Д.-Г .; Schoffeniels, E. (1977). «Молекулярные события и изменения энергии во время действия потенциала». PNAS. 74 (9): 3810–3813. Bibcode:1977ПНАС ... 74.3810М. Дои:10.1073 / пнас.74.9.3810. ЧВК  431740. PMID  71734.
4. Hasenstaub, A; Callaway, E; Отте, S; Сейновски, Т. (2010). «Метаболические затраты как объединяющий принцип, управляющий биофизикой нейронов». Труды Национальной академии наук США. 107 (27): 12329–12334. Bibcode:2010PNAS..10712329H. Дои:10.1073 / pnas.0914886107. ЧВК  2901447. PMID  20616090.
5. Тасаки, Ичиджи (13 октября 1995 г.). «Механические и тепловые изменения в электрическом органе торпеды, связанные с его постсинаптическими потенциалами». Сообщения о биохимических и биофизических исследованиях. 215 (2): 654–658. Дои:10.1006 / bbrc.1995.2514. PMID  7488005.
6. Ховарт, Дж. В .; Кейнс, Р. Д.; Ричи, Дж. М; Muralt, A von (1 июля 1975 г.). «Производство тепла, связанное с прохождением одиночного импульса в волокнах обонятельного нерва щуки» (PDF). Журнал физиологии. 249 (2): 349–368. Дои:10.1113 / jphysiol.1975.sp011019. ЧВК  1309578. PMID  1236946.
7. Тасаки, я; Бирн, П. М. (1993). «Быстрое выделение тепла, связанное с электрическим возбуждением электрических органов электрического угря». Biochem Biophys Res Commun. 197 (2): 910–915. Дои:10.1006 / bbrc.1993.2565. PMID  8267630.
8. Тасаки, К; Кусано, К; Бирн, П.М. (1989). «Быстрые термические и механические изменения обонятельного нерва саргана, связанные с распространяющимся импульсом». Biophys J. 55 (6): 1033–1040. Bibcode:1989BpJ .... 55.1033T. Дои:10.1016 / с0006-3495 (89) 82902-9. ЧВК  1330571. PMID  2765644.
9. Ховарт, Дж. В. (1975). «Производство тепла в немиелинизированных нервах». Философские труды Королевского общества. 270 (908): 425–432. Bibcode:1975РСПТБ.270..425Х. Дои:10.1098 / рстб.1975.0020. JSTOR  2417341. PMID  238239.
10. Тасаки, Ичиджи (1982). Физиология и электрохимия нервных волокон. Бетесда, Мэриленд: Academic Press Inc. (Лондон). ISBN  978-0-12-683780-3.
11. Кауфманн, Конрад (1989). Потенциалы действия и электрохимическая связь в макроскопической хиральной фосфолипидной мембране. Каруару, Бразилия.
12. Синь-И, Ван (1985). «Уединенная волна и неравновесный фазовый переход в жидких кристаллах». Физический обзор A. 32 (5): 3126–3129. Bibcode:1985PhRvA..32.3126X. Дои:10.1103 / PhysRevA.32.3126. PMID  9896466.
13. Хаймбург, Т., Джексон, А. Д. (12 июля 2005 г.). «О распространении солитонов в биомембранах и нервах». Proc. Natl. Акад. Sci. СОЕДИНЕННЫЕ ШТАТЫ АМЕРИКИ. 102 (2): 9790–9795. Bibcode:2005PNAS..102.9790H. Дои:10.1073 / pnas.0503823102. ЧВК  1175000. PMID  15994235.
14. Хаймбург, Т., Джексон, А.Д. (2007). «О потенциале действия как распространяющемся импульсе плотности и роли анестетиков». Биофиз. Rev. Lett. 2: 57–78. arXiv:физика / 0610117. Bibcode:2006физика..10117H. Дои:10.1142 / S179304800700043X.
15. Андерсен, С.С.Л., Джексон, А.Д., Хаймбург, Т. (2009). «К термодинамической теории распространения нервных импульсов». Прог. Нейробиол. 88 (2): 104–113. Дои:10.1016 / j.pneurobio.2009.03.002. PMID  19482227.^{[мертвая ссылка ]}
16. Griesbauer, J; Боссингер, S; Уиксфорт, А; Шнайдер, М. (9 мая 2012 г.). "Распространение 2D импульсов давления в липидных монослоях и его возможное значение для биологии". Письма с физическими проверками. 108 (19): 198103. arXiv:1211.4104. Bibcode:2012ПхРвЛ.108с8103Г. Дои:10.1103 / PhysRevLett.108.198103. PMID  23003093.
17. Шривастава, Шамит; Шнайдер, Маттиас (18 июня 2014 г.). «Доказательства наличия двумерных одиночных звуковых волн в интерфейсе, контролируемом липидами, и его значение для биологической передачи сигналов». Журнал интерфейса Королевского общества. 11 (97): 20140098. Дои:10.1098 / rsif.2014.0098. ЧВК  4078894. PMID  24942845.
18. Griesbauer, J; Боссингер, S; Уиксфорт, А; Шнайдер, М. (19 декабря 2012 г.). «Одновременно распространяющиеся импульсы напряжения и давления в липидных монослоях свиного мозга и синтетических липидах». Физический обзор E. 86 (6): 061909. arXiv:1211.4105. Bibcode:2012PhRvE..86f1909G. Дои:10.1103 / PhysRevE.86.061909. PMID  23367978.
19. Шривастава, Шамит (январь 2014 г.). НЕЛИНЕЙНЫЕ ОДИНОЧНЫЕ ЗВУКОВЫЕ ВОЛНЫ В ЛИПИДНЫХ МЕМБРАНАХ И ИХ ВОЗМОЖНАЯ РОЛЬ В БИОЛОГИЧЕСКОЙ СИГНАЛИЗАЦИИ (1-е изд.). Бостон, Массачусетс 02215 США: Диссертация, Бостонский университет.
20. Эбботт, Б.С., Хилл, А.В., Ховарт, Дж. В. (1958). «Положительное и отрицательное тепло, связанное с нервным импульсом». Труды Королевского общества B. 148 (931): 149–187. Bibcode:1958RSPSB.148..149A. Дои:10.1098 / rspb.1958.0012. PMID  13518134.
21. Иваса, К., Тасаки И., Гиббонс, Р. (1980). «Набухание нервных волокон, связанное с потенциалами действия». Наука. 210 (4467): 338–9. Bibcode:1980Sci ... 210..338I. Дои:10.1126 / science.7423196. PMID  7423196.
22. Griesbauer, J; Уиксфорт, А; Schneider, M F (15 ноября 2009 г.). «Распространение волн в липидных монослоях». Биофизический журнал. 97 (10): 2710–2716. Bibcode:2009BpJ .... 97.2710G. Дои:10.1016 / j.bpj.2009.07.049. ЧВК  2776282. PMID  19917224.
23. Виллагран Варгас, Э., Луду, А., Хустерт, Р., Гумрих, П., Джексон, А.Д., Хаймбург, Т. (2011). «Периодические решения и рефрактерные периоды в солитонной теории нервов и бедренного нерва саранчи». Биофизическая химия. 153 (2–3): 159–167. arXiv:1006.3281. Дои:10.1016 / j.bpc.2010.11.001. PMID  21177017.
24. Хаймбург, Т. (2010). «Липид-ионные каналы». Биофиз. Chem. 150 (1–3): 2–22. arXiv:1001.2524. Bibcode:2010arXiv1001.2524H. Дои:10.1016 / j.bpc.2010.02.018. PMID  20385440.
25. Хаймбург, Т., Джексон, А.Д. (2007). «Термодинамика общей анестезии». Биофиз. J. 92 (9): 3159–65. arXiv:физика / 0610147. Bibcode:2007BpJ .... 92.3159H. Дои:10.1529 / biophysj.106.099754. ЧВК  1852341. PMID  17293400.
26. Rall, W и Shepherd, GM (1968) Теоретические реконструкции дендродендритных синаптических взаимодействий в обонятельной луковице. J Нейрофизиол 31, 884-915.http://jn.physiology.org/content/jn/31/6/884.full.pdf
27. Ходжкина; Кац (1949). «Влияние температуры на электрическую активность гигантского аксона кальмара». J. Physiol. 109 (1–2): 240–249. Дои:10.1113 / jphysiol.1949.sp004388. ЧВК  1392577. PMID  15394322.
28. Тасаки, Ичиджи (1949). «Столкновение двух нервных импульсов в нервном волокне». Biochim Biophys Acta. 3: 494–497. Дои:10.1016/0006-3002(49)90121-3.
29. Гонсалес, Альфредо; Будвытите, Римма; Мосгаард, Ларс Д.; Ниссен, Сорен; Хаймбург, Томас (10 сентября 2014 г.). «Проникновение потенциалов действия во время столкновения в срединных и боковых гигантских аксонах беспозвоночных». Физический обзор X. 4 (3): 031047. arXiv:1404.3643. Bibcode:2014PhRvX ... 4c1047G. Дои:10.1103 / PhysRevX.4.031047.
30. Сандер, Х.В., Коллизионные испытания при заболеваниях периферических нервов Дж. Кимуры https://books.google.com/books?id=jp05zU9vxo8C&pg=PA359&lpg=PA359&dq=collision+test+neurophysiology&source=bl&ots=PTz3H5Mn-t&sig=LUtPKvs1ad8q0wX8zIQ712mNG7E&hl=en&sa=X&ei=dE9iVfvlENOMyASFz4OQAg&ved=0CB0Q6AEwADgK#v=onepage&q=collision%20test% 20 нейрофизиология & f = ложь
31. Eckl, C; Mayer, AP; Ковалев А С (3 августа 1998 г.). «Существуют ли поверхностные акустические солитоны?». Письма с физическими проверками. 81 (5): 983–986. Bibcode:1998PhRvL..81..983E. Дои:10.1103 / PhysRevLett.81.983.
32. Шривастава, Шамит; Канг, Кевин; Шнайдер, Маттиас Ф (30 января 2015 г.). «Уединенные ударные волны и адиабатический фазовый переход в липидных границах раздела и нервах». Физический обзор E. 91 (12715): 012715. arXiv:1411.2454. Bibcode:2015PhRvE..91a2715S. Дои:10.1103 / PhysRevE.91.012715. PMID  25679650.
33. Хилле, Бертил (2001). Ионные каналы возбудимых мембран (3-е изд. Ред.). Сандерленд, Массачусетс: Синауэр. ISBN  9780878933211.
34. Каттералл, Вашингтон (2014). «Структура и функция потенциалзависимых натриевых каналов при атомном разрешении». Экспериментальная физиология. 99 (1): 35–51. Дои:10.1113 / expphysiol.2013.071969. ЧВК  3885250. PMID  24097157.
35. Эль-Хади, А., Махта, Б. (2015). «Механические поверхностные волны сопровождают распространение потенциала действия». Nature Communications. 6: 6697. arXiv:1407.7600. Bibcode:2015 НатКо ... 6.6697E. Дои:10.1038 / ncomms7697. PMID  25819404.