Курносый ромбокубооктаэдр - Snub rhombicuboctahedron

Курносый ромбокубооктаэдр
Символ Шлефли	srr {4,3} = ${\displaystyle sr{\begin{Bmatrix}4\\3\end{Bmatrix}}}$
Обозначение Конвея	САК
Лица	74: 8+48 {3} 6+12 {4}
Края	120
Вершины	48
Группа симметрии	О, [4,3]^+, (432) порядок 24
Двойной многогранник	Пятиугольный тетраконтоктаэдр
Характеристики	выпуклый, хиральный

В курносый ромбокубооктаэдр это многогранник, построенный как усеченный ромбокубооктаэдр. У него 74 грани: 18 квадратов и 56 треугольников. Его также можно назвать Конвей курносый кубооктаэдр в, но будет перепутан с Coxeter курносый кубооктаэдр, то курносый куб.

Связанные многогранники

В курносый ромбокубооктаэдр можно увидеть в последовательности операций из кубооктаэдр.

Имя	Кубокта- эдр	Усеченный кубокта- эдр	Курносый кубокта- эдр	Усеченный ромбовидный кубокта- эдр	Курносый ромбовидный кубокта- эдр
Coxeter	CO (rC)	тСО (трК)	sCO (srC)	trCO (trrC)	srCO (htrrC)
Конвей	AC	taC = bC	СК	taaC = baC	САК
Изображение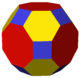
Конвей	jC	mC	gC	МАК	gaC
Двойной

Смотрите также

• Расширенный кубооктаэдр
• Усеченный ромбикосододекаэдр

Рекомендации

• Джон Х. Конвей, Хайди Берджель, Хаим Гудман-Штраус, Симметрии вещей 2008, ISBN  978-1-56881-220-5

внешняя ссылка

• Переводчик Джорджа Харта Конвея: порождает многогранники в VRML, принимая нотацию Конвея в качестве входных данных