Кодирование Слепяна – Вольфа - Slepian–Wolf coding

В теория информации и коммуникация, то Кодирование Слепяна – Вольфа, также известный как Слепиан – Волк, является результатом распределенное исходное кодирование обнаружен Давид Слепян и Джек Вольф в 1973 г. Это метод теоретической кодирование два сжатие без потерь коррелированный источники.^[1]

Настройка проблемы

Распределенное кодирование - это кодирование двух, в данном случае или более зависимых источников, с отдельными кодировщиками и совместным декодер. Учитывая два статистически зависимых i.i.d. случайный конечный алфавит последовательности ${\displaystyle X^{n}}$ и ${\displaystyle Y^{n}}$, теорема Слепяна – Вольфа дает теоретическую оценку скорости кодирования без потерь для распределенного кодирования двух источников.

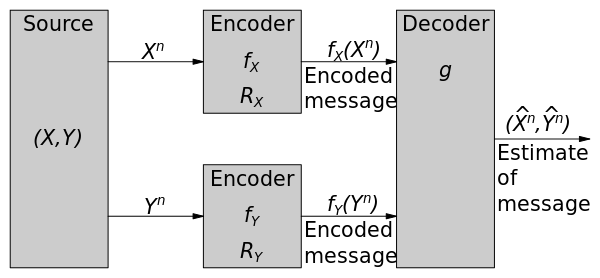
Теорема

Граница для скоростей кодирования без потерь, как показано ниже:^[1]

${\displaystyle R_{X}\geq H(X|Y),\,}$

${\displaystyle R_{Y}\geq H(Y|X),\,}$

${\displaystyle R_{X}+R_{Y}\geq H(X,Y).\,}$

Если и кодер, и декодер двух источников независимы, самая низкая скорость, которую он может достичь для сжатия без потерь, будет ${\displaystyle H(X)}$ и ${\displaystyle H(Y)}$ за ${\displaystyle X}$ и ${\displaystyle Y}$ соответственно, где ${\displaystyle H(X)}$ и ${\displaystyle H(Y)}$ энтропии ${\displaystyle X}$ и ${\displaystyle Y}$. Однако при совместном декодировании, если для длинных последовательностей принимается исчезающая вероятность ошибки, теорема Слепяна – Вольфа показывает, что может быть достигнута гораздо лучшая степень сжатия. Пока общая ставка ${\displaystyle X}$ и ${\displaystyle Y}$ больше их совместной энтропии ${\displaystyle H(X,Y)}$ и ни один из источников не кодируется со скоростью меньше, чем его энтропия распределенное кодирование может достигать сколь угодно малых вероятность ошибки для длинных последовательностей.^[1]

Особым случаем распределенного кодирования является сжатие с дополнительной информацией декодера, где источник ${\displaystyle Y}$ доступен на стороне декодера, но недоступен на стороне кодера. Это можно рассматривать как условие, при котором ${\displaystyle R_{Y}=H(Y)}$ уже использовался для кодирования ${\displaystyle Y}$, а мы намерены использовать ${\displaystyle H(X|Y)}$ закодировать ${\displaystyle X}$. Другими словами, два изолированных источника могут сжимать данные так же эффективно, как если бы они обменивались данными друг с другом. Вся система работает асимметрично (степень сжатия для двух источников асимметрична).^[1]

Эта оценка была расширена на случай более чем двух коррелированных источников Томас М. Обложка в 1975 г.^[2] и аналогичные результаты были получены в 1976 г. Аарон Д. Уайнер и Джейкоб Зив в отношении кодирования с потерями совместных гауссовских источников.^[3]

Смотрите также

• Сжатие данных
• Синхронизация данных
  • Синхронизация (информатика)
• ОБСУЖДЕНИЕ
• Хронология теории информации

Рекомендации

1. Слепян и Волк 1973 С. 471–480.
2. Обложка 1975 С. 226–228.
3. Винер и Зив 1976, стр. 1–10.

Источники

• Обложка, Томас М. (Март 1975 г.). «Доказательство теоремы сжатия данных Слепяна и Вольфа для эргодических источников» Т. ». IEEE Transactions по теории информации. 21 (2): 226–228. Дои:10.1109 / TIT.1975.1055356. ISSN  0018-9448.
• Слепян, Дэвид С.; Вольф, Джек К. (Июль 1973 г.). «Бесшумное кодирование коррелированных источников информации». IEEE Transactions по теории информации. 19 (4): 471–480. Дои:10.1109 / TIT.1973.1055037. ISSN  0018-9448.
• Винер, Аарон Д.; Зив, Джейкоб (Январь 1976 г.). «Функция скорости искажения для кодирования источника с дополнительной информацией в декодере». IEEE Transactions по теории информации. 22 (1): 1–10. CiteSeerX  10.1.1.137.494. Дои:10.1109 / TIT.1976.1055508. ISSN  0018-9448.

внешняя ссылка

• Кодирование видео по Виннер-Зиву алгоритм сжатия видео, близкий к границе Слепяна – Вольфа (со ссылками на исходный код).