Проекции на выпуклые множества - Projections onto convex sets
Эта статья может быть сбивает с толку или неясно читателям. (Апрель 2018 г.) (Узнайте, как и когда удалить этот шаблон сообщения) |
В математике проекции на выпуклые множества (POCS), иногда называемый переменная проекция метод, это метод поиска точки на пересечении двух закрыто выпуклый наборы. Это очень простой алгоритм, который переоткрывался много раз.[1] Самый простой случай, когда наборы аффинные пространства, был проанализирован Джон фон Нейман.[2][3] Случай, когда множества являются аффинными пространствами, является особым, поскольку итерации не только сходятся к точке на пересечении (при условии, что пересечение непусто), но и к ортогональной проекции точки на пересечение. Для общих замкнутых выпуклых множеств предельная точка не обязательно должна быть проекцией. Классическая работа над случаем двух замкнутых выпуклых множеств показывает, что скорость сходимости итераций линейно.[4][5]Теперь есть расширения, которые рассматривают случаи, когда существует более одного набора, или когда наборы не выпуклый,[6] или которые обеспечивают более высокую скорость сходимости. Анализ POCS и связанных методов пытается показать, что алгоритм сходится (и если да, найти скорость сходимости ) и сходится ли она к проекция исходной точки. Эти вопросы в основном известны для простых случаев, но являются предметом активных исследований для расширений. Также существуют варианты алгоритма, такие как Алгоритм проектирования Дикстры. См. Ссылки в дальнейшее чтение раздел для обзора вариантов, расширений и приложений метода POCS; хороший исторический фон можно найти в разделе III.[7]
Алгоритм
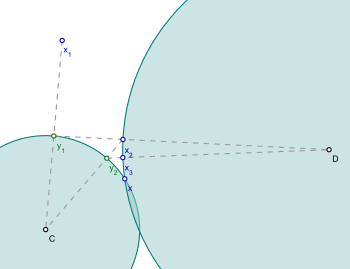
Алгоритм POCS решает следующую проблему:
куда C и D находятся закрыто выпуклые множества.
Чтобы использовать алгоритм POCS, нужно знать, как проецировать на наборы C и D отдельно.Алгоритм начинается с произвольного значения для а затем генерирует последовательность
Простота алгоритма частично объясняет его популярность. Если пересечение из C и D непусто, то последовательность сгенерированный алгоритмом будет сходиться в какой-то момент на этом перекрестке.
В отличие от Алгоритм проектирования Дикстры, решение не обязательно должно быть проекцией на пересечение C и D.
Связанные алгоритмы

Методика усредненные прогнозы очень похоже. Для случая двух замкнутых выпуклых множеств C и D, он продолжается
Давно известно о глобальном сближении.[8] Более того, этот метод легко обобщить более чем на два набора; некоторые результаты сходимости для этого случая есть.[9]
В усредненный метод прогнозов можно переформулировать как чередование метод проекций с использованием стандартного приема. Рассмотрим множество
который определен в пространство продукта . Затем определите другой набор, также в области продукта:
Таким образом, находя эквивалентно поиску .
Чтобы найти точку в используйте метод попеременного проецирования. Проекция вектора на съемочную площадку F дан кем-то . Следовательно
С и предполагая , тогда для всех , и, следовательно, мы можем упростить итерацию до .
Рекомендации
- ^ Bauschke, H.H .; Борвейн, Дж. М. (1996). «О проекционных алгоритмах решения задач выпуклой допустимости». SIAM Обзор. 38 (3): 367–426. CiteSeerX 10.1.1.49.4940. Дои:10.1137 / S0036144593251710.
- ^ Дж. Фон Нейман,Нойман, Джон Фон (1949). «О кольцах операторов. Теория редукции». Анна. математики. 50 (2): 401–485. Дои:10.2307/1969463. JSTOR 1969463. (перепечатка конспектов лекций, впервые распространенная в 1933 г.)
- ^ Дж. Фон Нейман. Функциональные операторы, том II. Princeton University Press, Princeton, NJ, 1950. Перепечатка записанных на мимеографе конспектов лекций, впервые распространенных в 1933 г.
- ^ Губин, Л.Г .; Поляк, Б.Т .; Райк, Э. (1967). «Метод проекций для нахождения точки пересечения выпуклых множеств». СССР Вычислительная математика и математическая физика. 7 (6): 1–24. Дои:10.1016/0041-5553(67)90113-9.
- ^ Bauschke, H.H .; Борвейн, Дж. М. (1993). «О сходимости алгоритма альтернативной проекции фон Неймана для двух множеств». Установленный анализ. 1 (2): 185–212. Дои:10.1007 / bf01027691.
- ^ Lewis, A. S .; Малик, Дж. (2008). «Знакопеременные проекции на многообразиях». Математика исследования операций. 33: 216–234. CiteSeerX 10.1.1.416.6182. Дои:10.1287 / moor.1070.0291.
- ^ Комбетс, П. Л. (1993). «Основы теоретико-множественного оценивания» (PDF). Труды IEEE. 81 (2): 182–208. Дои:10.1109/5.214546. Архивировано из оригинал (PDF) на 2015-06-14. Получено 2012-10-09.
- ^ А. Ауслендер. Числовые методы для решения проблем оптимизации с ограничениями. Кандидатская диссертация, Факультет наук, Гренобль, 1969 г.
- ^ Локальная сходимость для чередующихся и усредненных невыпуклых проекций. А. Льюис, Р. Люк, Дж. Малик, 2007. arXiv
дальнейшее чтение
- Книга с 2011 года: Альтернативные методы проецирования Рене Эскаланте и Маркос Райдан (2011), опубликовано SIAM.
















