Периферийный цикл - Peripheral cycle
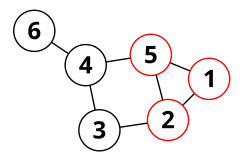
В теория графов, а периферический цикл (или же периферийная цепь) в неориентированный граф Интуитивно это цикл, который не отделяет какую-либо часть графа от других частей. Периферийные циклы (или, как их изначально называли, периферийные полигоны, поскольку Тутт называл циклы "многоугольниками") впервые были изучены Тутт (1963), и играют важную роль в характеристике планарные графы и в создании велосипедные пространства неплоских графов.[1]
Определения
Периферический цикл в графике можно формально определить одним из нескольких эквивалентных способов:
- периферийный, если это простой цикл в связный граф со свойством, что для каждых двух ребер и в , существует путь в что начинается с , заканчивается на , и не имеет внутренних вершин, принадлежащих .[2]
- периферийный, если это индуцированный цикл со свойством, что подграф образованный удалением ребер и вершин подключен.[3]
- Если любой подграф , а мост[4] из минимальный подграф из который не пересекается ребром с и у этого есть свойство, что все его точки присоединения (вершины, смежные с ребрами в обоих и ) принадлежать .[5] Простой цикл является периферийным, если у него ровно один мост.[6]
Эквивалентность этих определений нетрудно увидеть: связный подграф (вместе с краями, связывающими его с ), или аккорд цикла, который вызывает его сбой, должен в любом случае быть мостом, а также должен быть класс эквивалентности из бинарное отношение на ребрах, в которых два ребра связаны, если они являются концами пути без внутренних вершин в .[7]
Характеристики
Периферийные циклы появляются в теории многогранные графы, то есть, 3-вершинно-связанный планарные графы. Для каждого плоского графа , и каждое плоское вложение , грани вложения, являющиеся индуцированными циклами, должны быть периферийными циклами. В многогранном графе все грани являются периферийными циклами, а каждый периферийный цикл - гранью.[8] Из этого факта следует, что (с точностью до комбинаторной эквивалентности, выбора внешней грани и ориентации плоскости) каждый многогранный граф имеет единственное плоское вложение.[9]
В плоских графах велосипедное пространство порождается гранями, но в неплоских графах периферийные циклы играют аналогичную роль: для каждого конечного графа с 3-вершинной связью пространство циклов порождается периферийными циклами.[10] Результат также можно распространить на локально конечные, но бесконечные графы.[11] В частности, отсюда следует, что 3-связные графы гарантированно содержат периферийные циклы. Существуют двухсвязные графы, не содержащие периферийных циклов (например, полный двудольный граф , для которого каждый цикл имеет два моста), но если двусвязный граф имеет минимальную степень три, то он содержит хотя бы один периферийный цикл.[12]
Периферийные циклы в 3-связных графах могут быть вычислены за линейное время и используются для разработки тестов на планарность.[13]Они также были распространены на более общее понятие неразложимых разложений уха. В некоторых алгоритмах проверки планарности графов полезно найти цикл, который не является периферийным, чтобы разбить проблему на более мелкие подзадачи. В двусвязном графе звание цепи меньше трех (например, график цикла или же тета-график ) каждый цикл является периферийным, но каждый двусвязный граф с рангом схемы три или более имеет непериферийный цикл, который можно найти за линейное время.[14]
Обобщая хордовые графы, Сеймур и Уивер (1984) определить задушенный граф быть графом, в котором каждый периферийный цикл представляет собой треугольник. Они характеризуют эти графики как кликовые суммы хордовых графов и максимальные планарные графы.[15]
Связанные понятия
Периферийные циклы также называются неразрывными циклами,[2] но этот термин неоднозначен, так как он также использовался для двух связанных, но различных концепций: простых циклов, удаление которых отключило бы оставшийся граф,[16] и циклы топологически вложенный граф таким образом, чтобы разрезание по циклу не отключало поверхность, на которую встроен граф.[17]
В матроиды, неразрывной схемой называется схема матроида (то есть минимального зависимого множества) такая, что удаление схема оставляет подключенный матроид меньшего размера (то есть, который не может быть записан как прямая сумма матроидов).[18] Они аналогичны периферийным циклам, но не одинаковы даже в графические матроиды (матроиды, схемы которых являются простыми циклами графа). Например, в полный двудольный граф , каждый цикл является периферийным (у него только один мост, двухреберный путь), но графический матроид, образованный этим мостом, не подключен, поэтому никакая схема графического матроида не разделяет.
Рекомендации
- ^ Тутте, В. Т. (1963), «Как нарисовать график», Труды Лондонского математического общества, Третья серия, 13: 743–767, Дои:10.1112 / плмс / с3-13.1.743, МИСТЕР 0158387.
- ^ а б Ди Баттиста, Джузеппе; Идс, Питер; Тамассия, Роберто; Толлис, Иоаннис Г. (1998), Рисование графиков: алгоритмы визуализации графиков, Prentice Hall, стр. 74–75, ISBN 978-0-13-301615-4.
- ^ По сути, это определение, используемое Брун (2004). Однако Брун выделяет случай, когда имеет изолированные вершины от разрывов, вызванных удалением .
- ^ Не путать с мост (теория графов), другое понятие.
- ^ Тутте, В. Т. (1960), «Выпуклые представления графов», Труды Лондонского математического общества, Третья серия, 10: 304–320, Дои:10.1112 / плмс / с3-10.1.304, МИСТЕР 0114774.
- ^ Это определение периферийных циклов, первоначально использовавшееся Тутт (1963). Сеймур и Уивер (1984) используйте то же определение периферийного цикла, но с другим определением моста, которое больше напоминает определение индуцированного цикла для периферийных циклов.
- ^ См. Например Теорема 2.4 из Тутт (1960), показывающее, что множества вершин мостов линейно связны, см. Сеймур и Уивер (1984) для определения мостов, использующих хорды и компоненты связности, а также см. Di Battista et al. (1998) для определения мостов с использованием классов эквивалентности бинарного отношения на ребрах.
- ^ Тутт (1963), Теоремы 2.7 и 2.8.
- ^ См. Примечания после теоремы 2.8 в Тутт (1963). Как замечает Тутте, об этом уже знали Уитни, Хасслер (1932), «Неразделимые и плоские графы», Труды Американского математического общества, 34 (2): 339–362, Дои:10.2307/1989545, МИСТЕР 1501641.
- ^ Тутт (1963), Теорема 2.5.
- ^ Брун, Хеннинг (2004), «Цикловое пространство 3-связного локально конечного графа порождается его конечными и бесконечными периферийными схемами», Журнал комбинаторной теории, Серия B, 92 (2): 235–256, Дои:10.1016 / j.jctb.2004.03.005, МИСТЕР 2099143.
- ^ Томассен, Карстен; Тофт, Бьярн (1981), "Неразрывные индуцированные циклы в графах", Журнал комбинаторной теории, Серия B, 31 (2): 199–224, Дои:10.1016 / S0095-8956 (81) 80025-1, МИСТЕР 0630983.
- ^ Шмидт, Йенс М. (2014), «Последовательность Mondshein», Конспект лекций по информатике: 967–978, Дои:10.1007/978-3-662-43948-7_80.
- ^ Di Battista et al. (1998), Лемма 3.4, с. 75–76.
- ^ Сеймур, П. Д.; Уивер, Р. В. (1984), "Обобщение хордовых графов", Журнал теории графов, 8 (2): 241–251, Дои:10.1002 / jgt.3190080206, МИСТЕР 0742878.
- ^ Например. видеть Borse, Y.M .; Waphare, Б. Н. (2008), "Непересекающиеся неразделяющие циклы вершин в графах", Журнал Индийского математического общества, Новая серия, 75 (1–4): 75–92 (2009), МИСТЕР 2662989.
- ^ Например. видеть Кабельо, Серджио; Мохар, Боян (2007), «Поиск кратчайших неразрывных и несжимаемых циклов для топологически вложенных графов», Дискретная и вычислительная геометрия, 37 (2): 213–235, Дои:10.1007 / s00454-006-1292-5, МИСТЕР 2295054.
- ^ Майя, Браулио, младший; Лемос, Маноэль; Мело, Тереза Р. Б. (2007), "Неразрывные схемы и кокосхемы в матроидах", Комбинаторика, сложность и случайность, Oxford Lecture Ser. Математика. Appl., 34, Оксфорд: Oxford Univ. Press, стр. 162–171, Дои:10.1093 / acprof: oso / 9780198571278.003.0010, МИСТЕР 2314567.









