Правила Полингса - Paulings rules

Правила Полинга пять правил опубликованы Линус Полинг в 1929 г. для предсказание и рационализация кристаллические структуры из ионные соединения.^[1]^[2]

Первое правило: правило отношения радиусов

Для типичных ионных твердых веществ катионы меньше, чем анионы, и каждый катион окружен согласованный анионы, образующие многогранник. Сумма ионные радиусы определяет расстояние катион-анион, а отношение радиусов катионов и анионов ${ displaystyle r _ {+} / r _ {-}}$ (или же ${ displaystyle r_ {c} / r_ {a}}$ ) определяет координационный номер (C.N.) катиона, а также форму согласованного многогранника анионов.^[3]^[4]

Для координационных чисел и соответствующих многогранников в таблице ниже Полинг математически вывел минимум отношение радиусов, при котором катион контактирует с заданным числом анионов (рассматривая ионы как жесткие сферы). Если катион меньше, он не будет контактировать с анионами, что приведет к нестабильности, ведущей к более низкому координационному числу.

Коэффициент критического радиуса. Эта диаграмма предназначена для координационного числа шесть: 4 аниона в показанной плоскости, 1 над плоскостью и 1 под ней. Предел устойчивости находится при r_C/р_А = 0.414

Соотношение многогранника и минимального радиуса для каждого координационного числа
C.N.	Многогранник	Коэффициент радиуса
3	треугольный	0.155
4	тетраэдр	0.225
6	октаэдр	0.414
7	покрытый октаэдром	0.592
8	квадратная антипризма (антикуб)	0.645
8	куб	0.732
9	трехугольная призма	0.732
12	кубооктаэдр	1.00

Три диаграммы справа соответствуют октаэдрической координации с координационным числом шесть: четыре аниона в плоскости диаграмм и два (не показаны) выше и ниже этой плоскости. На центральной диаграмме показано минимальное отношение радиусов. Катион и любые два аниона образуют прямоугольный треугольник, с ${ displaystyle 2r _ {-} = { sqrt {2}} (r _ {-} + r _ {+})}$ , или же ${ displaystyle { sqrt {2}} r _ {-} = r _ {-} + r _ {+}}$ . потом ${ displaystyle r _ {+} = ({ sqrt {2}} - 1) r _ {-} = 0,414r _ {-}}$ . Подобные геометрические доказательства дают минимальные отношения радиусов для высокосимметричных случаев C.N. = 3, 4 и 8.^[5]

Кристаллическая структура NaCl. Каждый атом Na имеет шесть ближайших соседей с октаэдрической геометрией.

Элементарная ячейка CsCl. Каждый атом Cs имеет восемь ближайших соседей с кубической геометрией.

Для C.N. = 6 и отношение радиусов больше минимума, кристалл более устойчив, поскольку катион все еще находится в контакте с шестью анионами, но анионы находятся дальше друг от друга, так что их взаимное отталкивание уменьшается. Октаэдр может тогда образоваться с отношением радиусов больше или равным 0,414, но когда отношение поднимается выше 0,732, кубическая геометрия становится более стабильной. Это объясняет, почему Na⁺ в NaCl с отношением радиусов 0,55 имеет октаэдрическую координацию, тогда как Cs⁺ в CsCl с отношением радиусов 0,93 имеет кубическую координацию.^[6]

Если отношение радиусов меньше минимального, два аниона будут стремиться уйти, а оставшиеся четыре перестроятся в тетраэдрическую геометрию, где все они будут в контакте с катионом.

Правила отношения радиусов - это первое приближение, которое позволяет успешно предсказывать координационные числа, но существует множество исключений.^[4]

Второе правило: правило электростатической валентности

Для данного катиона Полинг определил^[2] то сила электростатической связи к каждому координированному аниону как ${ displaystyle s = { frac {z} { nu}}}$ , где z - заряд катиона, ν - координационное число катиона. Стабильная ионная структура устроена так, чтобы сохранять местная электронейтральность, так что сумма сил электростатических связей с анионом равна обвинять на этот анион.

{ Displaystyle xi = сумма _ {я} s_ {я}}

куда ${ Displaystyle xi}$ - заряд аниона, суммирование ведется по соседним катионам. Для простых твердых тел ${ displaystyle s_ {i}}$ одинаковы для всех катионов, координированных с данным анионом, так что координационное число аниона представляет собой заряд аниона, деленный на каждую силу электростатической связи. Некоторые примеры приведены в таблице.

Катионы с оксидом O²⁻ ион
Катион	Коэффициент радиуса	Катион C.N.	Электростатический прочность сцепления	Анион С.Н.
Ли⁺	0.34	4	0.25	8
Mg²⁺	0.47	6	0.33	6
Sc³⁺	0.60	6	0.5	4

Полинг показал, что это правило полезно для ограничения возможных структур для более сложных кристаллов, таких как алюмосиликат минеральная ортоклаз, КАЛСИ₃О₈, с тремя разными катионами.^[2]

Третье правило: разделение углов, ребер и граней многогранника

Совместное использование ребер и особенно граней двух анионных полиэдров снижает стабильность ионной структуры. Совместное использование углов не так сильно снижает стабильность, поэтому (например) октаэдры могут иметь общие углы друг с другом.^[7]

Уменьшение стабильности происходит из-за того, что общие края и грани помещают катионы ближе друг к другу, так что электростатическое отталкивание катионов увеличивается. Эффект наиболее велик для катионов с высоким зарядом и низким C.N. (особенно когда r + / r- приближается к нижнему пределу полиэдральной устойчивости).

В качестве одного из примеров Полинг рассмотрел три минеральные формы оксид титана, каждое с координационным числом 6 для Ti⁴⁺ катионы. Самая стабильная (и самая распространенная) форма - это рутил, в котором координационные октаэдры расположены так, что каждый из них имеет только два ребра (и не имеет граней) с соседними октаэдрами. Две другие, менее стабильные формы Brookite и анатаз, в котором каждый октаэдр имеет три и четыре ребра, соответственно, с соседними октаэдрами.^[7]

Правило четвертое: кристаллы, содержащие разные катионы

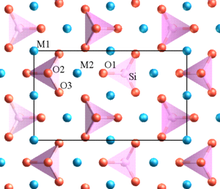
Состав оливина. M (Mg или Fe) = синие сферы, Si = розовые тетраэдры, O = красные сферы.

В кристалл содержащие различные катионы, имеющие высокие валентность и малое координационное число имеют тенденцию не разделять элементы многогранников друг с другом.^[8] Это правило имеет тенденцию увеличивать расстояние между сильно заряженными катионами, чтобы уменьшить электростатическое отталкивание между ними.

Один из примеров Полинга: оливин, М₂SiO₄, где M - смесь Mg²⁺ на некоторых сайтах и Fe²⁺ у других. В структуре присутствуют отчетливые SiO₄ тетраэдры, которые не имеют общих атомов кислорода (в углах, краях или гранях) друг с другом. Низковалентный Mg²⁺ и Fe²⁺ катионы окружены многогранниками, которые имеют общие атомы кислорода.

Пятое правило: правило бережливости

Количество существенно различных видов составляющих в кристалле обычно невелико. Повторяющиеся единицы будут иметь тенденцию быть идентичными, потому что каждый атом в структуре наиболее стабилен в определенной среде. Может быть два или три типа многогранников, например тетраэдры или октаэдры, но разных типов не будет.